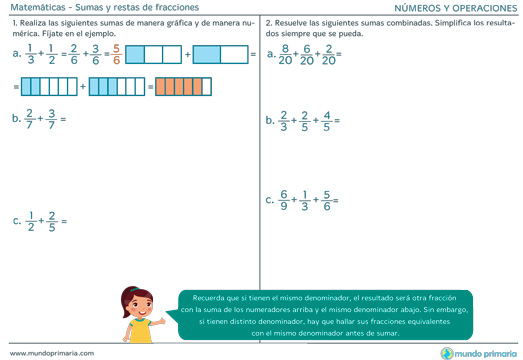
Suma y resta de fracciones
Vamos a ver en este artículo dos de las operaciones básicas que podemos realizar con las fracciones: la suma y la resta.
Verás que, para cada una de ellas es importante fijarnos en el denominador, ya que no se realizan igual las sumas y restas de fracciones si tienen el mismo denominador o si éste es distinto.
Suma de fracciones
A la hora de sumar fracciones conviene trabajar con dos casos. El primero es cuando las fracciones tienen el mismo denominador. Y el segundo es aquel en el que las fracciones poseen denominadores distintos.
Suma de fracciones con igual denominador
Es muy fácil hacer la adición de fracciones con igual denominador, debido a que en este caso agregamos partes de objetos del mismo tipo. En este apartado vamos a estudiar cómo hacer esta operación de forma gráfica, en la recta numérica y de manera analítica.
Vamos a sumar 15 + 35 .
Lo primero que haremos será representar gráficamente las fracciones.
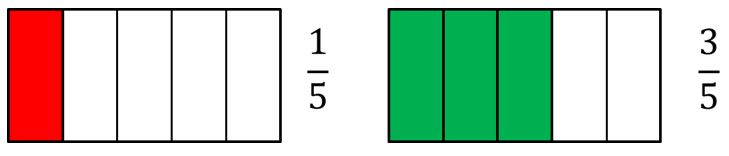
Ahora juntemos las porciones de la unidad representadas en color rojo y verde. Recuerda que es posible unir estas porciones, porque ambas fracciones están denominadas en quintos.
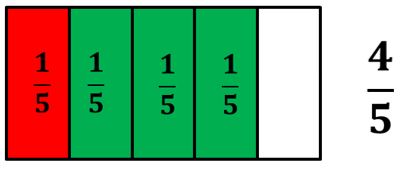
Al juntar las fracciones 15 y 35 se obtiene como resultado 45 . Es decir, que:
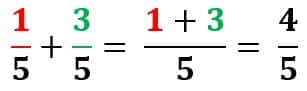
Para sumar fracciones de igual denominador se suman los numeradores y se conservan los denominadores.
Ahora representemos la adicción 26+16+56 en la recta numérica:
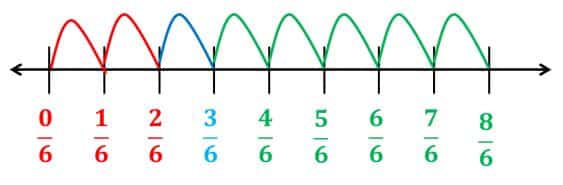
Fíjate que la suma de 26+16+ 56 la podemos realizar representándola en la recta numérica.
Para llamar la suma, suponemos que damos de salteo de 16 en 16 .
Primero damos 26de salto, luego 16de salto y, por último, 56de salto. Al final llegamos a 86 que es el resultado de sumar 26+16+56 .
Adición de fracciones con distinto denominador
La adición de fracciones con distinto denominador es posible efectuarla mediante al menos tres procedimientos distintos: el método gráfico, el de las fracciones equivalentes y el del mínimo común múltiplo. Conocerlos es muy importante porque incrementa la comprensión acerca de esta operación y el concepto de fracción.
Método gráfico para sumar fracciones de distinto denominador
Ahora sumaremos fracciones con distinto denominador, para ello aplicaremos primero el principio de las fracciones equivalentes.
Supongamos que deseamos obtener la suma de 25+14, esto es:
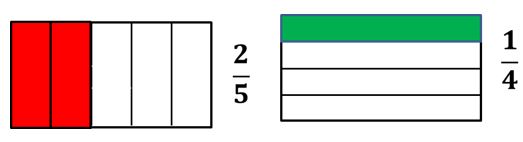 | Representando gráficamente las fracciones dadas. |
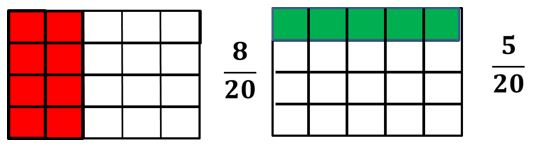 | Dividimos los quintos en cuartos y los cuartos en quintos. |
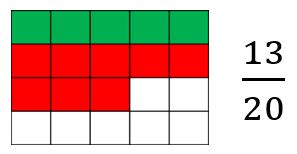 | Agregamos los 520 a los 820 y obtenemos 1320. |
Método de las fracciones equivalentes para sumar fracciones
| OPERACIÓN | EXPLICACIÓN |
| 25+14=2×45×4+1×54×5 | 25y14 se sustituyen por las fracciones equivalentes, 2×45×4y1×54×5 respectivamente. |
| 25+14=820+520 | 820y520 representan las fracciones 25y14. |
| 25+14=8+520 | Ya podemos obtener la suma de 25y14 . |
| 25+14=1320 | Obtenemos como resultado 1320. |
Método del mínimo común múltiplo para la suma de fracciones.
Cuando se deben sumar dos fracciones el principio de las fracciones equivalentes es sencillo y eficiente. Al ser más de dos conviene aplicar el método del mínimo común múltiplo.
Veamos un ejemplo:
Vamos a sumar: 32+712+ 1115
Los números 2, 12 y 15 son los denominadores de las fracciones a sumar, son diferentes entre sí y poseen divisores comunes entre sí.
Vamos a descomponer en factores primos estos números para determinar el mínimo común múltiplo de 2, 12 y 15, es decir el mcm(2, 12, 15). Veamos:
1. Para calcular el mínimo común múltiplo lo primero que haremos será descomponer los números en factores primos. Esto es:
| 2 = 2¹ | 12=2x2x2 = 2² x3 | 15 = 5 x 3 |
Ahora escogemos los factores comunes y no comunes con su mayor exponente
mcm(2, 12, 15) = 22 x 3 x 5 = 2 x 2 x 3 x 5 = 60
2. Este mínimo común múltiplo de los denominadores será el nuevo común denominador de las tres fracciones.
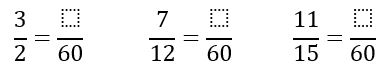
3. Ahora dividimos el denominador común entre el denominador original de cada fracción, y luego multiplicamos por el numerador el número resultante en cada caso:
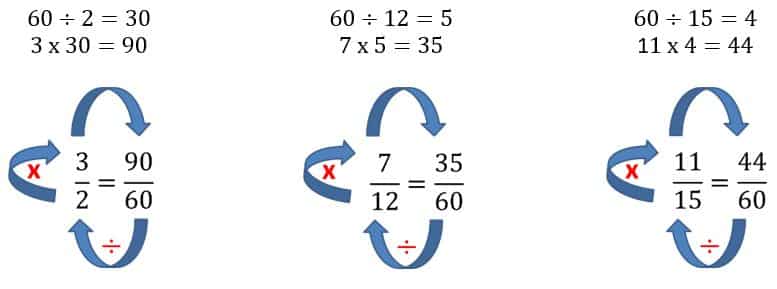
4. Sustituimos las fracciones originales por las equivalentes que acabamos de encontrar:
32+712+ 1115= 9060+3560+ 4460
5. Por último, se suman los numeradores y se conserva el denominador de las fracciones:
32+712+ 1115= 9060+3560+ 4460=90+35+4460= 16960
Problemas de suma de fracciones
A continuación se presentan dos problemas en los que se aplica la de adición de fracciones.
1. Un recipiente se llena con el contenido de tres envases. Si la capacidad de los tres envases es 34l, 1 12 l, 2 14 l. ¿Cuál es la capacidad del recipiente?
Para conocer la capacidad del recipiente debemos sumar la capacidad de los tres envases. Veamos:
| OPERACIÓN | EXPLICACIÓN |
| 34+ 112+ 214= 34+32+94 | Se sustituyen los números mixtos 112y 214 por las fracciones impropias 32y 94 respectivamente. |
| 34+ 112+ 214= 3+6+94 | Aplicamos el método del mínimo común múltiplo para sumar fracciones. |
| 34+ 112+ 214= 184 | Resolviendo la adición que queda expresada en el numerador. |
| 34+ 112+ 214= 92 | Simplificando 184= 92. |
De acuerdo con el resultado de la adición el recipiente tiene una capacidad de 92litros.
2. Una llave ha llenado 18 de un tanque de agua, otra ha llenado 12 y una tercera 14. ¿Qué fracción del tanque queda por llenar?
Este problema lo podemos resolver con tan sólo hacer una representación gráfica como la siguiente:
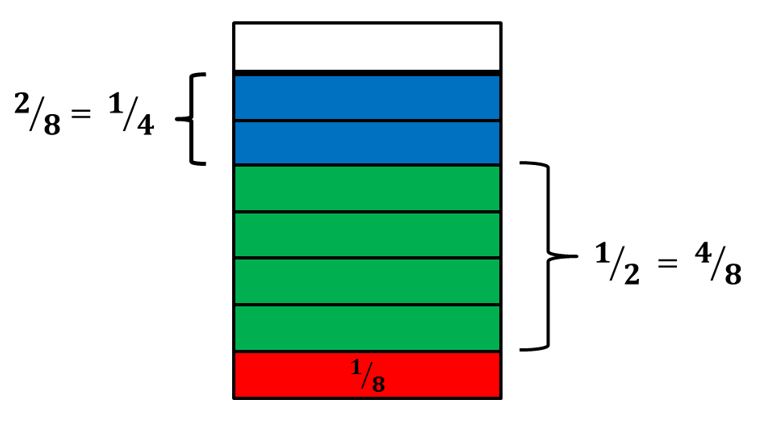
En el gráfico se observa que el tanque ha quedado dividido en octavos, siendo 14= 28 y 12= 48 , por lo que para conocer que fracción del tanque se ha llenado sólo tendríamos que sumar 18+48+ 28. Veamos:
| OPERACIÓN | EXPLICACIÓN |
| 18+ 12+ 14= 18+48+28 | Sustituyendo 18, 12, 14 por sus fracciones equivalentes correspondientes 18, 48, 28. |
| 18+ 12+ 14= 1+4+28 | Aplicando el principio de la suma de fracciones con igual denominador. |
| 18+ 12+ 14= 78 | El resultado que se obtiene es 78. |
En la representación gráfica se puede notar que la fracción del tanque que falta por llenar es 18.
También, podemos hacerlo de forma analítica, es decir, le restamos a la unidad 78.
Veamos:
| OPERACIÓN | EXPLICACIÓN |
| 1-78= 88–78 | Sustituyendo la unidad por la fracción 88. |
| 1-78= 18 | Restando fracciones con igual denominador. El resultado es 18. |
Después de realizar las operaciones queda claro que la fracción del tanque que falta por llenar es 18.
Resta de fracciones
La sustracción de fracciones es una operación que se realiza de forma sencilla, y que ayuda a eliminar o reducir una cantidad específica que está expresada en fracciones.
Existen dos casos para la sustracción de fracciones:
- Sustracción de fracciones con igual denominador.
- Sustracción de fracciones con distinto denominador.
Veamos cómo hacer para realizar la sustracción de fracciones en cada caso.
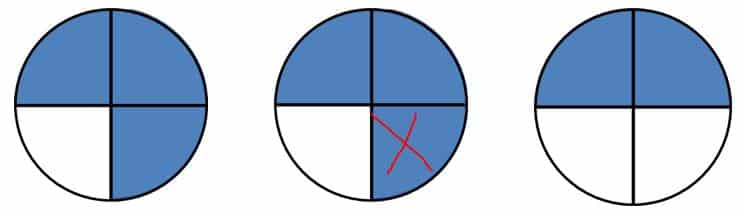
Sustracción de fracciones de igual denominador
De forma gráfica tenemos lo siguiente:
| 34 | 14 | 24 |
 | ||
Ahora de forma analítica nos queda:
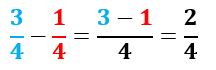
Resta de fracciones de igual denominador en la recta numérica
También es posible representar esta sustracción en la recta numérica. Veamos:
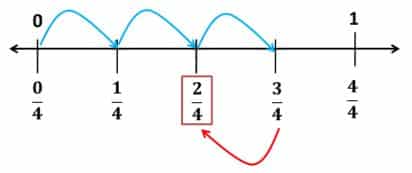
En la siguiente representación gráfica podemos observar la idea de resta como diferencia de fracciones.
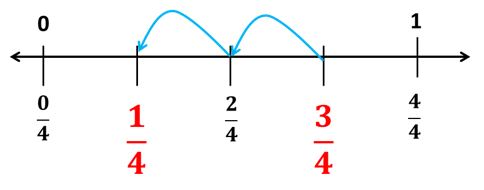
Vemos que la diferencia entre 34 y 14 es igual a 24.
Resta de fracciones con diferente denominador
La sustracción de fracciones con distinto denominador sigue un proceso similar al de la adición de fracciones cuando sus denominadores son diferentes.
La fracción resultante de la sustracción tendrá como denominador el denominador común y como numerador la diferencia de ambos numeradores.
Ejemplo: Veamos cómo se realiza esta sustracción: 45 – 23
De forma gráfica sería así:
- Se representan ambas fracciones

- Se llevan ambas fracciones a un denominador común. Para ello dividimos en 3 partes iguales los cuatro quintos y en cinco partes iguales los dos tercios. Nos queda lo siguiente:

- Ahora si podemos restarle 10 quinceavos a 12 quinceavos:
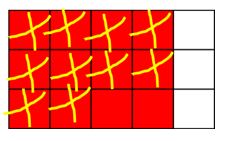
- El resultado de la sustracción es el siguiente:
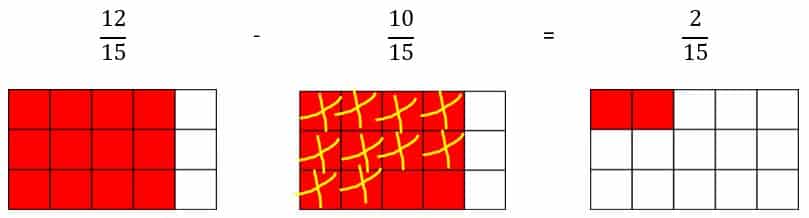
Ahora vamos a resolverla de forma analítica, con el método de las fracciones equivalentes:
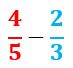
1. Amplificamos cada fracción por el denominador de la otra fracción. Es decir que amplificaremos a 45 por 3 y a 23 por 5. Nos quedan así:
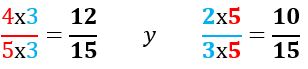
2. Ahora restamos las fracciones equivalentes resultantes:
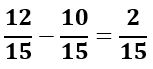
Como ves, obtenemos el mismo resultado por ambos métodos.
Método del mínimo común múltiplo para restar fracciones
Para restar un par de fracciones el método de amplificación funciona muy bien. Sin embargo, es recomendable emplear el método del mínimo común múltiplo obtener fracciones un poco más simplificadas como resultado.
Veamos un ejemplo de cómo funciona este método resolviendo la siguiente sustracción:
58–712
1. Primero buscamos el mínimo común múltiplo de los denominadores.
En este caso sería el mínimo común múltiplo de 8 y 12, que se escribe mcm(8,12). Para ello descomponemos cada uno en factores primos:
8 = 2³ y 12 = 3 x 2²
El mínimo común múltiplo de 8 y 12 es el producto de los factores primos comunes y no comunes con su mayor exponente.
mcm (8, 12) = 3 x 2³ = 3 x 8 = 24
2. Ahora usamos este mínimo común múltiplo como nuevo denominador de las fracciones:
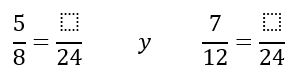
3. Para conseguir los numeradores dividimos 24 entre el numerador anterior, y luego multiplicamos el resultado por el numerador. Esto lo hacemos para cada fracción:
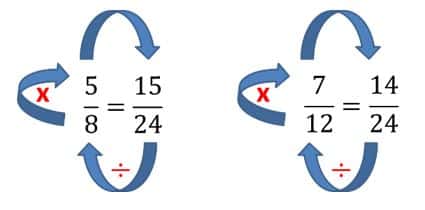
Han quedado fracciones de igual denominador, que son equivalentes a las fracciones iniciales.
4. Ahora realizamos la sustracción con estas fracciones que hemos encontrado:
58–712=1524–1424=124
De esta manera resolvimos la sustracción de fracciones con diferente denominador usando el mínimo común múltiplo de los denominadores, nos quedó:
58–712=124
Problemas con sustracción de fracciones
Aquí presentamos algunos problemas de aplicación de sustracción de fracciones:
Problema 1: Lucía tiene12kg de azúcar. Si usa tres octavos octavos de ella, ¿cuánto le quedará de azúcar?
- Veamos los datos que tenemos y establecemos la operación a realizar:
Cantidad que tiene Lucía: 12Kg de azúcar.
Cantidad que usa: 38Kg de azúcar.
Queremos saber cuánta azúcar le quedará, por lo que debemos restar la cantidad de azúcar que tiene menos la cantidad de azúcar que usa.
Es decir, resolveremos 12–38
- Realizamos la operación empleando el método de mínimo común múltiplo.
- Buscamos el mínimo común múltiplo de 2 y 8. Es decir, mcm (2,8). Para ello, descomponemos los denominadores en factores primos:
2 = 2¹ y 8 = 2³
- Tomamos los factores comunes y no comunes con su mayor exponente, y vemos que el mínimo común múltiplo es 8, es decir que mcm(2,8)=8.
- Ahora 8 es el nuevo denominador común de ambas fracciones. Fíjate que ya tres octavos tiene a 8 como denominador, por eso quedará igual:
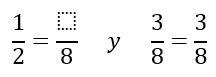
- Aplicamos el método para buscar el numerador de la fracción equivalente a 12
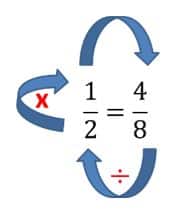
- Ahora realizamos la resta:
12–38=48–38=18
- Respondemos a la pregunta ¿cuánto le quedará de azúcar?:
A Lucía le quedará 18 kg de azúcar.
Problema 2: ¿Cuál número debemos sumar a 12 para que nos de 67 ?
- En este caso debemos ver la sustracción como la diferencia entre dos fracciones.
De manera que lo que queremos es saber cuánto le falta a 12 para llegar a 67 .
- Para poder hacer la sustracción, y así conocer la diferencia entre estas dos fracciones, vamos a llevarlas al mismo denominador buscando el mínimo común múltiplo de los denominadores, que son 2 y 7.
Como ambos son números primos, al descomponerlos quedan:
2 = 2 x 1 y 7 = 7 x 1
Por lo que mcm(2,7)= 2×7=14
- Aplicamos el método y realizamos la resta:

1214–714=514
- Ahora respondemos a la pregunta planteada, a 12debemos sumarle514 para que nos de67 .
- Comprobemos:
| OPERACIÓN | EXPLICACIÓN |
| 12+ 514= 714+514 | Por ser mcm(2,14)=14. Y aplicando el método del mínimo común múltiplo. |
| 12+ 514= 1214 | Sumando las fracciones equivalentes 714y514 . |
| 12+ 514= 67 | Simplificando 1214. |
Te dejamos unas actividades para que puedas practicar lo aprendido:
Selecciona un juego 👇 👇 👇

Con el mismo denominador 1

Con el mismo denominador 2

Con el mismo denominador 3

Con distinto denominador 1

Con distinto denominador 2

Cuestionario

Con el mismo denominador 1

Con el mismo denominador 2

Con el mismo denominador 3

Con distinto denominador 1

Con distinto denominador 2

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.