Puedes poner a prueba tus conocimientos iniciales con este cuestionario. No te preocupes si no sale del todo bien, puedes volver a hacerlo más adelante, cuando hayas terminado de leer el artículo.
¿Qué son las fracciones equivalentes?
Este tema de las fracciones equivalentes para niños es muy interesante porque en algunas ocasiones podemos estar refiriéndonos a la misma porción de una unidad y llamarla de distintas maneras.
Las fracciones equivalentes representan la misma porción de la unidad, aunque no tengan el mismo número en el numerador y en el denominador.
En esta sección te mostraremos que cuando hablamos de “un medio”, “dos cuartos” o “cuatro octavos” de un objeto, nos estamos refiriendo a la misma porción de ese objeto.
Ejemplos de fracciones equivalentes:
En una pastelería venden una deliciosa tarta redonda con forma de flor.
Esa tarta la compraron en casa de Jorge, en casa de Miguel y en casa de María.
En cada casa decidieron cortarla para obtener cierto número de pedazos y regalar algunos, siempre cuidando que cada porción sea del mismo tamaño.
Veamos cómo picaron la tarta en cada casa:
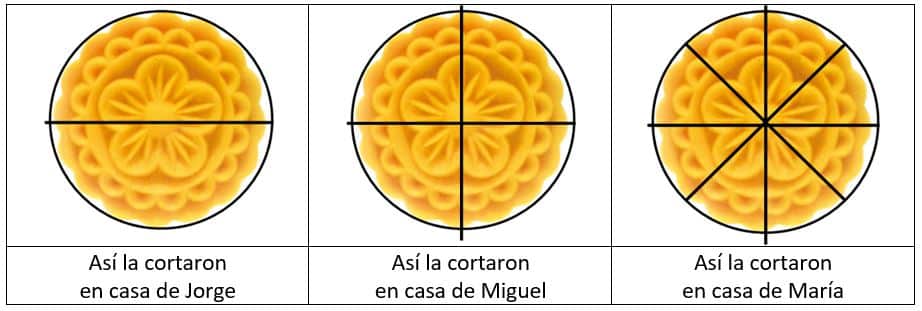
En casa de Jorge la cortaron en 2 partes iguales y regalaron 1 de esas mitades a la abuelita de Jorge que vive cerca.
En casa de Miguel la picaron en 4 pedazos iguales y regalaron 2 de esos pedazos a su primo Carlos para que lo comiera de postre con su tía Ángela.
Y en la casa de María cortaron la tarta en 8 porciones iguales y regalaron 4 de estas porciones a las amiguitas de María que estaban de visita esa tarde.
Veamos cómo quedan las tartas si los pedazos que regalaron los coloreamos de rojo:
Veamos cómo se representa en fracciones la parte de la tarta que regalaron en cada casa:
Como puedes observar, la parte de la tarta que regalaron en cada una de las casas es la misma, de manera que estas fracciones son equivalentes.
12 = 24 = 48
Ejemplos gráficos de fracciones equivalentes:
Estas fracciones representan la misma porción de la unidad:
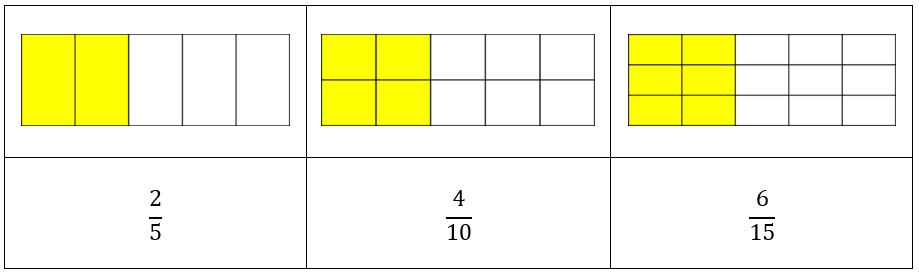
Entonces decimos que son equivalentes, es decir, dos quintos es igual a cuatro décimos e igual a seis quinceavos.
25 = 410 = 615
Observa cada una de las gráficas:
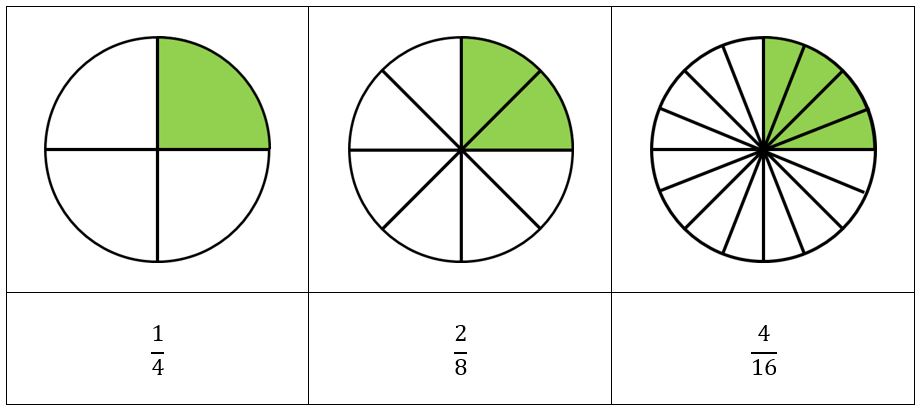
Aquí podemos observar que las fracciones 14 , 28 y 416 son equivalentes, o, lo que es lo mismo que un cuarto es igual a dos octavos e igual a cuatro dieciseisavos:
14 = 28 = 416
Método numérico para fracciones equivalentes
No siempre tenemos que representar gráficamente las fracciones para ver si son equivalentes.
Existe un método que permite verificarlo de la siguiente manera:
Digamos que queremos saber si 28 es equivalente a 416 .
Entonces hacemos la llamada «multiplicación cruzada» de la siguiente manera:
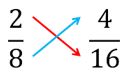
Obtenemos los productos siguientes:
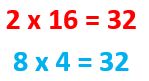
Si los «productos cruzados» son iguales, como en este caso, entonces las fracciones son equivalentes.
Pero si los «productos cruzados» son diferentes entonces las fracciones no son equivalentes.
Por último, decimos que la fracción dos octavos es equivalente a la fracción cuatro dieciseisavos.
28 = 416
Veamos un par de ejemplos de cómo funciona este método:
¿Es 26 equivalente a 14 ?
Veámoslo de forma numérica:
Obtenemos el producto cruzado de los numeradores y los denominadores:
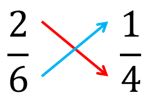
Nos queda:
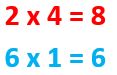
Al finarnos en los resultados vemos que son distintos, de manera que no son equivalentes estas fracciones.
Concluimos que dos sextos no es equivalente a un cuarto.
28 ≠ 416
Observa cómo se ven gráficamente:
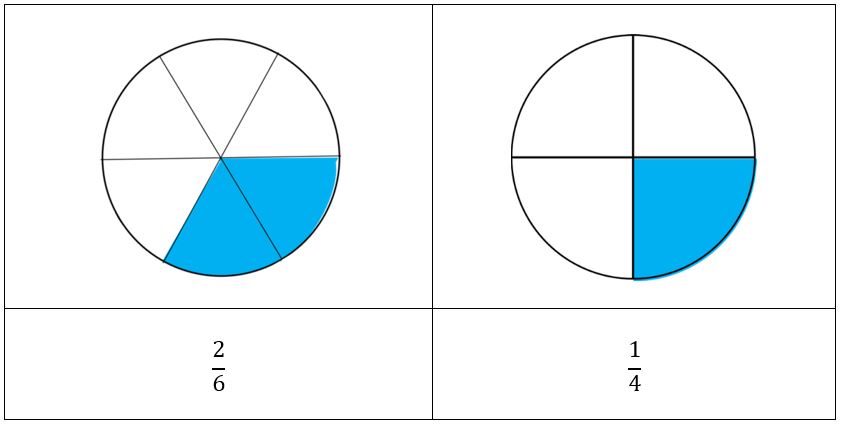
Comprobamos así que estas dos fracciones representan porciones distintas de la unidad. Por lo tanto, no son equivalentes.
¿Es 35 equivalente a 915 ?
Calculamos el producto cruzado de los numeradores y denominadores:
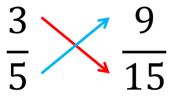
Nos resulta lo siguiente:
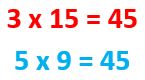
Al observar los resultados nos damos cuenta que son iguales. Entonces las fracciones son equivalentes.
Podemos afirmar que tres quintos es equivalente a nueve quinceavos.
Si queremos representarlos gráficamente se vería así:
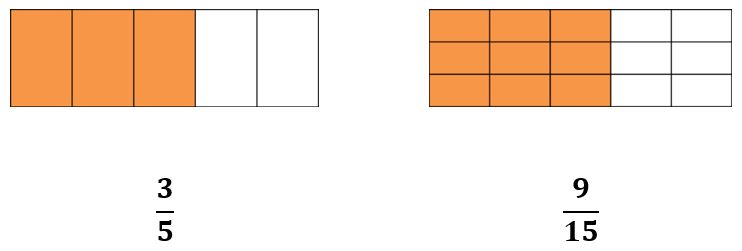
Amplificación y simplificación de fracciones
Como ya sabes, existen las fracciones equivalentes que, aunque son distintas, representan la misma porción de la unidad.
Ahora bien, podemos encontrar fracciones equivalentes usando métodos de amplificación o métodos de simplificación de fracciones, según nos convenga más para operar con ellas.
La simplificación de fracciones consiste en conseguir una fracción equivalente a la que nos han dado pero con números menores a los que tiene la fracción inicial en el numerador y en el denominador.
Por ejemplo, 13es una fracción simplificada de 721.
La amplificación de fracciones, por su parte, se emplea para conseguir fracciones equivalentes con números mayores en el numerador y en el denominador que en los de la fracción inicial.
Por ejemplo, 416es una fracción amplificada de 14.
Método para simplificar fracciones
Vamos a ver primero la manera de simplificar fracciones de forma gráfica. Tomaremos como ejemplo la fracción 721
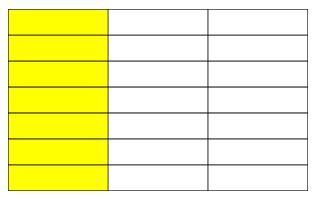
Tal como su significado lo indica, simplificar quiere decir hacer algo más simple, más sencillo.
En este caso vamos a simplificar la cantidad de divisiones que se ve en la gráfica pero que siga manteniendo el concepto de fracción en su esencia. Es decir:
Que quede dividida en partes iguales.
Que la porción resaltada quede contenida perfectamente en una o varias de estas partes.
Ahora bien, vamos a eliminar las divisiones horizontales para que nos queden tres partes iguales con las divisiones verticales:
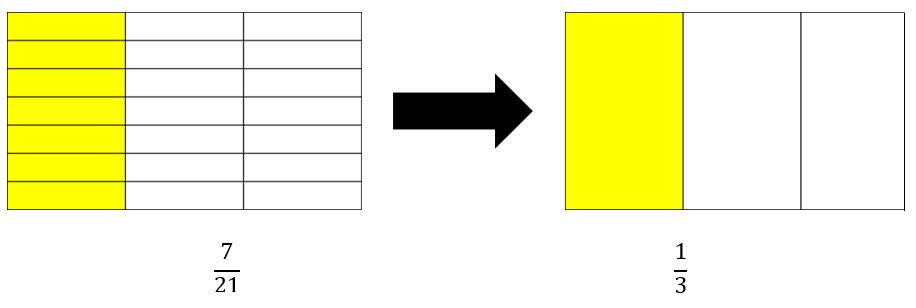
Vemos entonces que la fracción 721 quedó simplificada a 13 aplicando el método gráfico.
Ahora vamos a emplear el método numérico para la simplificación de fracciones a la misma fracción que tenemos como ejemplo, es decir a 721:
Tomamos el numerador y el denominador de la fracción, y vemos cuáles son los divisores comunes que tienen.
En este caso serían los divisores comunes de 7 y 21, que son el 1 y el 7.
Ahora tomamos el mayor de los divisores comunes, y dividimos tanto el numerador como el denominador por ese mismo número para obtener la fracción simplificada:
721=7÷721÷7=13
La fracción ha quedado simplificada en una fracción equivalente con números en el denominador y en el numerador que son menores a los iniciales:
721=13
Métodos para amplificar fracciones
Aquí también empezaremos con la forma gráfica para amplificación de fracciones, y tomaremos como ejemplo el procedimiento para amplificar14.
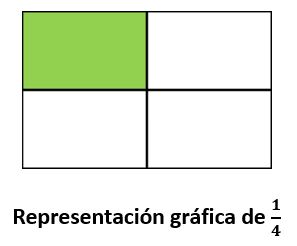
Ahora, ampliamos la cantidad de partes en la que se ha dividido la unidad, cuidando que no pierda la condición de ser fracción, es decir que quede dividida en partes iguales.
Añadiremos dos divisiones más horizontales y dos divisiones más verticales. Veamos:
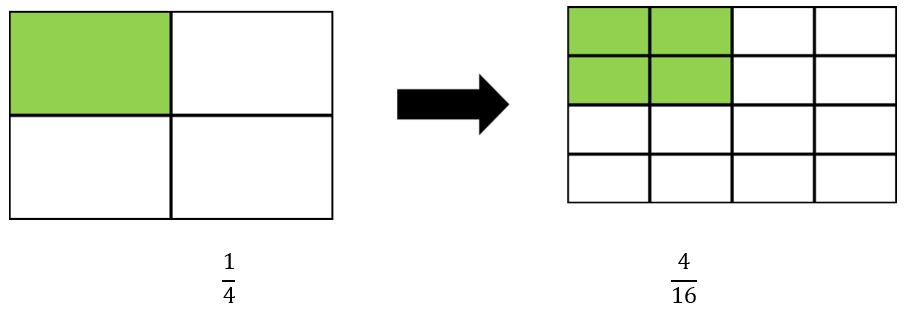
Hemos amplificado 14 a su equivalente 416 usando el método gráfico.
Ahora vamos a aprender el método numérico de amplificación de fracciones. Usaremos la misma fracción del ejemplo anterior.
Tomamos 14 y multiplicamos tanto el numerador como el denominador por el mismo número:
14=1×44×4=416
Ejercicios resueltos de simplificación de fracciones:
Simplificar las siguientes fracciones: a)1224 b)2849 c)1664
Soluciones:
a)1224
Buscamos los divisores comunes de 15 y 24, que son:
D(15, 24) = {1, 2, 3, 4, 6, 12}
Podemos simplificarla dividiendo el numerador y el denominador por cualquiera de estos números, pues son divisores comunes de ambos.
Vamos a tomar el mayor de los divisores comunes para obtener la fracción más simplificada, también llamada fracción irreductible:
1224=12÷1224÷12=12
Nos queda:
1224=12
b)2849
Encontramos los divisores comunes de 28 y 49. D(28,49) = {1, 7}
Dividimos numerador y denominador por el mismo número:
2849=28÷749÷7=47
Quedando:
2849=47
c)1664
Los divisores comunes de 16 y 64 son D(16,64)= {1, 2, 4, 8, 16}
Simplificamos por 16:
1664=16÷1664÷16=14
Obtenemos que:
1664=14
A continuación, te dejamos estas fichas para que practiques la amplificación y simplificación de fracciones:
Reducción a igual denominador
Este tema es muy importante para poder comparar, sumar y restar fracciones de distintos denominadores de forma sencilla. Por ello es fundamental su comprensión para poder avanzar en el conocimiento de las operaciones con fracciones de forma exitosa.
Llevar dos fracciones cualesquiera a igual denominador significa encontrar dos fracciones equivalentes a las dadas pero que tengan ambas el mismo denominador.
Un ejemplo de reducción de fracciones a igual denominador es el siguiente:
Tenemos este par de fracciones:
15y23
Sabemos que 15es equivalente a315 y que 23es equivalente a 1015.
Es decir que:
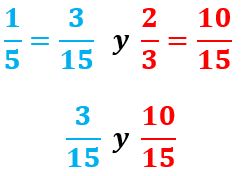
Como ves, ambas fracciones quedaron reducidas a igual denominador.
Ahora bien, ¿cuál es el procedimiento para reducir estas fracciones a igual denominador?
Tenemos dos procedimientos para llevar fracciones a igual denominador:
El procedimiento gráfico.
El procedimiento numérico.
Veremos primero en qué consiste el procedimiento gráfico.
Para ello tomemos como ejemplo las fracciones siguientes:
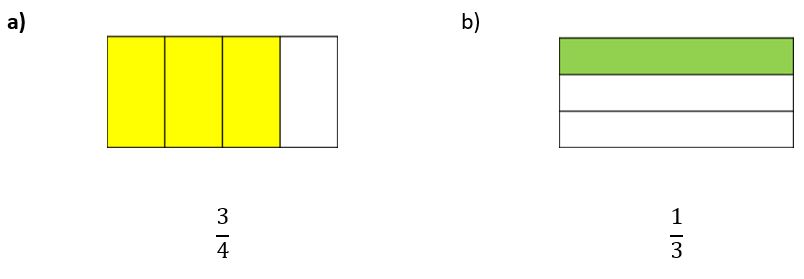
Fijémonos en los denominadores de ambas fracciones:
El denominador de la fracción a es 4.
El de la fracción b es 3.
Ahora vamos a dividir la fracción a en 3 partes iguales y a dividir la fracción b en 4 partes iguales.
Es como si “cruzáramos” los denominadores para hacer una nueva representación de la misma porción de la unidad. Observa:
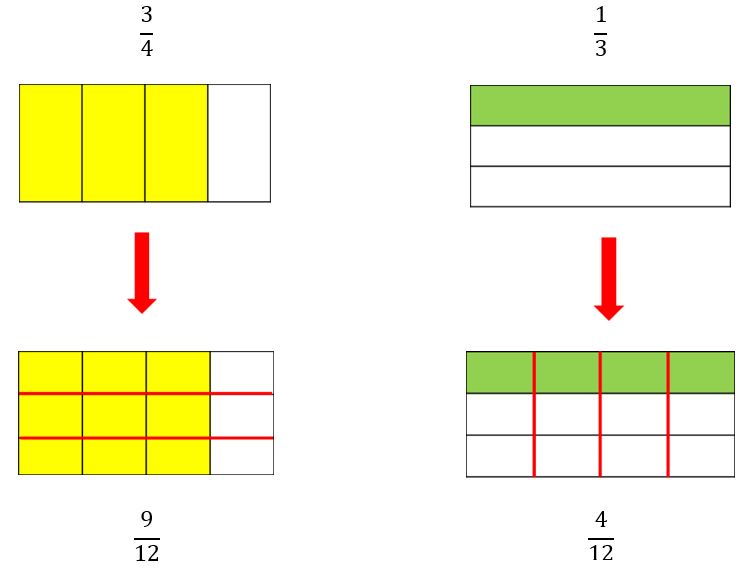
Tenemos ahora las fracciones iniciales llevadas a denominadores iguales:
34=912 y 13=412
Ahora veremos cuál es el método numérico para llevar fracciones al mismo denominador. Para ello usaremos las mismas fracciones 34y 13:
Tomaremos el denominador de cada una y amplificaremos la otra usando ese número.
Para 34 usaremos el 3 (que es el denominador de 13)
Para 13 usaremos el 4 (que es denominador de 34)
Amplificando cada fracción nos queda:
34=3x34x3=912
13=1x43x4=412
Estos métodos serán de mucha utilidad al sumar y restar fracciones.
Veamos algunos ejemplos:
Ejemplo 1:
Llevar45y12 a igual denominador.
Observamos ambos denominadores y buscamos el mínimo común múltiplo de ambos.
El mínimo común múltiplo de 5 y 2 es 10. Es decir m.c.m.(5,2) = 10.
Este mínimo común múltiplo será ahora el denominador común de ambas fracciones. Tenemos entonces:
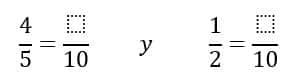
Ahora debemos calcular el numerador de ambas. Es importante recordar que la fracción resultante en cada caso debe ser equivalente a la original:
En el caso de 45 tenemos que ver por cuánto multiplicamos el 5 del denominador para que sea 10. Para ello resolvemos 10 ÷ 5 = 2
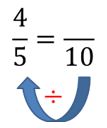
Luego multiplicamos el numerador por 2. Es decir, 4 x 2 = 8. Y ese es el denominador de la nueva fracción. Nos queda:
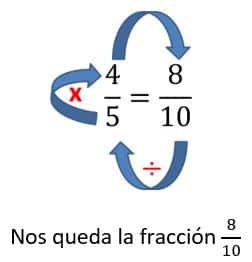
Aplicamos lo mismo para la fracción 12. En este caso, resolvemos 10 ÷ 2 = 5, y después multiplicamos 1 x 5 = 5.
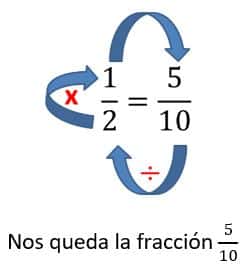
Ejemplo 2:
Llevar las fracciones28,34y56 a igual denominador común.
Buscamos el mínimo común múltiplo de los denominadores de las fracciones que son 8, 4 y 6.
Nos queda que m.c.m. (8,4,6)=24.
Este mínimo común múltiplo de los denominadores será el nuevo común denominador de las tres fracciones.
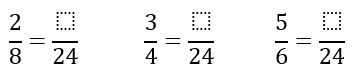
Ahora dividimos el denominador común entre el denominador original de cada fracción, y luego multiplicamos por el numerador el número resultante en cada caso:
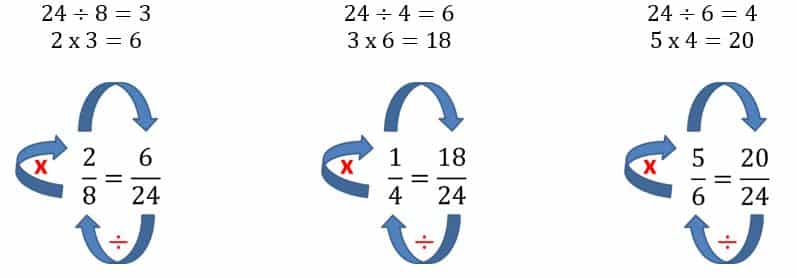
Las fracciones que nos resultaron son:
624—1824 —2024
A continuación, te dejamos esta ficha para que practiques la reducción de fracciones a común denominador:
Orden de las fracciones
Las fracciones representan cantidades, por lo que unas pueden representar más y otras menos. Es decir que algunas fracciones pueden ser mayores o menores que otras fracciones.
Entonces, es posible hablar de una relación de orden entre las fracciones. A continuación te enseñamos a comparar fracciones para reconocer cuál es mayor y cuál es menor, además de poder ordenarlas en forma creciente o decreciente, según lo requieras.
Para determinar si una fracción es mayor o menor que otra debemos compararlas.
En este artículo presentamos tres casos que te ayudarán a comparar fracciones.
Comparación de fracciones de igual denominador
Si dos o más fracciones tienen igual denominador, es mayor la que tiene mayor numerador.
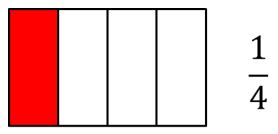
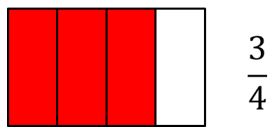
Supongamos que las fracciones que queremos comparar son 14y34.
Lo primero que haremos será representar gráficamente las fracciones 14y34.
En la representación se observa que la fracción 34 toma una porción de la unidad mayor a la que queda seleccionada cuando representamos 14.
Esta representación gráfica es una forma de visualizar que:
34 es mayor que14
También se puede escribir:
34>14
Otra manera de visualizar que 34 es mayor que14 es representando ambas fracciones en la recta numérica. Veamos:
Si suponemos que las fracciones 14y34 indican los saltos que debemos dar en la recta numérica. Entonces, nos damos cuenta que al saltar con la fracción 34 nos alejamos más del cero que saltando con la fracción 14.
Esto quiere decir que 34 nos permite recorrer mayor distancia en la recta numérica que 14.
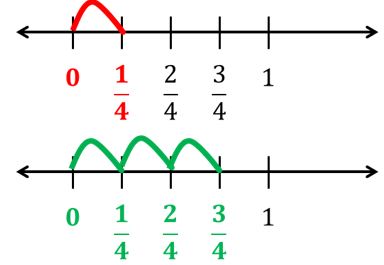
De esta manera se visualiza que 34 es mayor que14
También es posible establecer quién es mayor entre14y34relacionándola con un aspecto de la vida cotidiana.
Por ejemplo, supongamos que María compra 14 kg de queso, mientras que Juan compra 34 kg de queso. Si queremos saber quién compró más, entonces podemos establecer una tabla de equivalencia. Fíjate:
KILOGRAMOS (kg)
GRAMOS (g)
1
1.000
12
500
14
250
34
750
En la tabla se observa que 34 kg equivale a 750 g, mientras que 14 kg equivalen a 250 g.
Como 750 g es mayor que 250 g, se puede establecer que34 es mayor que14.
Para comparar las fracciones 14y34 hemos utilizado tres representaciones distintas, lo que nos ha permitido visualizar con total claridad que 34 es mayor que14 .
Si queremos visualizar la comparación de dos o más fracciones de igual denominador podemos apoyarnos en cualquiera de los tres procedimientos anteriores.
Comparación de fracciones de igual numerador
Si dos o más fracciones tienen igual numerador, es mayor la que tiene menor denominador.
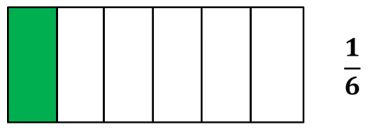
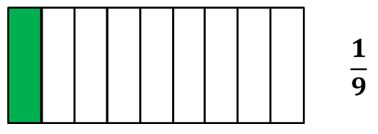
Vamos a comparar las fracciones 13—16 —19 para determinar cuál es mayor.
Representemos gráficamente las tres fracciones. La unidad de referencia será de igual tamaño en los tres casos.
Las tres fracciones tienen como numerador el uno. Fíjate que:
13es la fracción que toma una mayor porción de la unidad.
En segundo lugar se ubica 16.
Y, por último, tenemos a 19.
Esto quiere decir que:
13 es mayor que16 y 16 es mayor que19
En lenguaje simbólico se escribe:
13>16>19
Si comparamos las fracciones 13—16 —19 con la ayuda de la recta numérica resulta lo siguiente:
Suponiendo que damos saltos en la recta numérica, tenemos que el salto que nos permite alejarnos más del 0 es el que damos con la fracción 13.
El segundo salto más largo sería el de la fracción 16. Y de último quedaría el salto correspondiente a 19.
Esto quiere decir que, en este caso, la mayor distancia en la recta se alcanza con la fracción 13, seguida de la fracción 16, y en último lugar queda la fracción 19.
De esta forma se puede ver que:
13>16>19
Comparación de fracciones con numeradores y denominadores distintos
Vamos a comparar las fracciones 85—73 —54
Para realizar esta comparación, debemos encontrar fracciones equivalentes a las fracciones dadas, de tal modo que tengan el mismo denominador.
Vamos a realizarlo a partir de los siguientes pasos:
Determinamos el mínimo común múltiplo de los denominadores de las fracciones85—73 —54.
El procedimiento sería el siguiente:
Descomponemos en sus factores primos los denominadores. Esto es: 5 = 5, 3 = 3, 4 = 22.
A partir de la descomposición de los denominadores aplicamos la regla del mínimo común múltiplo, quedándonos que el mcm (3, 4, 5) = 60.
Este mínimo común múltiplo de los denominadores será el nuevo común denominador de las fracciones que se desean comparar.
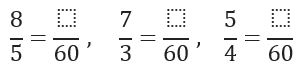
Seguidamente dividimos el denominador común entre el denominador original de cada fracción. Luego el resultado de cada división lo multiplicamos por el numerador de la fracción que corresponda.
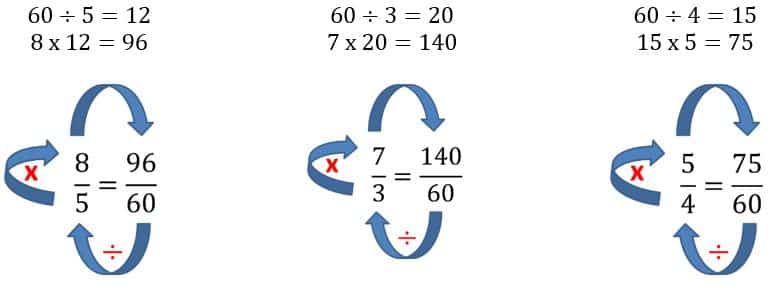
Las fracciones obtenidas con de igual denominador:
9660—14060 —7560
Ahora aplicamos el criterio de comparación de fracciones con igual denominador, el que nos dice: Si dos o más fracciones tienen igual denominador, es mayor la que tiene mayor numerador.
Entonces, en este caso la fracción mayor es 14060, seguida por 9660, y por último tenemos a 7560.
Utilizando el símbolo mayor que (>) tenemos: 14060>9660>756.
Volviendo a las fracciones originales 85—73 —54 y sabiendo que85=9660,73=14060,54=7560 .
Se tiene que: 73 es mayor que85 y 85 es mayor que54 .
Empleando el signo mayor que (>) quedaría así:
73>85>54
Aquí te dejamos estas actividades para practicar el orden de las fracciones:
Selecciona un juego 👇 👇 👇
Fracciones equivalentes 1
Fracciones equivalentes 2
Ampliación y simplificación de fracciones
Reducción a común denominador 1
Reducción a común denominador 2
Orden de las fracciones 1
Orden de las fracciones 2
Cuestionario
Para concluir, te dejamos un apunte en el que encontrarás la información más relevante del texto que te será útil para repasar y para realizar otros ejercicios que hagas.
Registrado en SafeCreative.