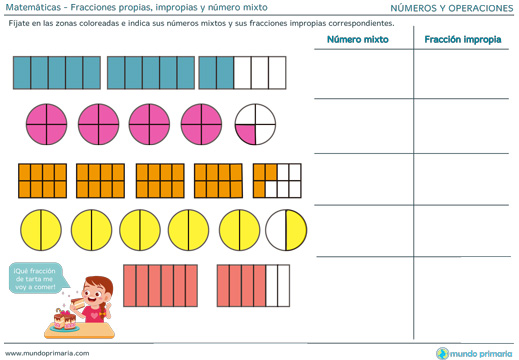
Fracciones propias, impropias y número mixto
En este artículo hablaremos de fracciones propias, impropias y número mixto. Esta manera de clasificar las fracciones se hace tomando como referencia la unidad, pues se establece que hay fracciones menores o mayores que la unidad.
Fracción propia
Algunos ejemplos de fracciones propias son:

Las fracciones propias son las primeras que conocemos en la escuela, generalmente se utilizan para iniciar el estudio de la noción de fracción. Esto se debe a que es sencilla de representar, visualizar y muy útil para la vida cotidiana.
Fracción impropia
Hay fracciones mayores que la unidad que se denominan fracciones impropias. Veamos su definición:
Estos son ejemplos de fracciones impropias:

Este concepto está estrechamente vinculado con la idea de número mixto. De hecho un número mixto siempre tiene una fracción impropia asociada y viceversa.
Pero qué es un número mixto. Veamos:
Número mixto
Algunos números mixtos son:
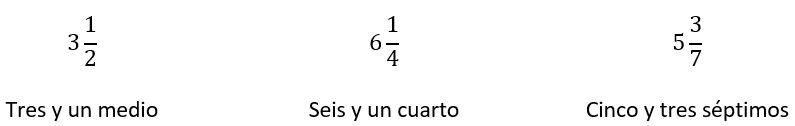
Son muchos los ejemplos de número mixto y su aplicación en muchas actividades como la cocina, pasando por la medicina y llegando hasta las medidas de las llaves que utilizan los mecánicos para reparar los vehículos.
Ejemplo de aplicación de fracciones propias, impropias y números mixtos:
La receta de María
María que vive con su esposo y sus dos hijos. Ella prepara ricas, variadas y saludables comidas.
A toda la familia le gustan los postres, la leche frita es la preferida de todos. Mira la receta de este exquisito manjar.
Ingredientes para 4 personas:
- 14 kg de azúcar.
- 1 12 l de leche.
- 18 kg de maicena.
- 4 yemas de huevo.
- 1 rama de canela.
- 1 cáscara de naranja.
- 1 12 limón.
- 4 Naranjas.
- 1 Huevo.
- Aceite de girasol.
- Harina.
Preparación de la receta:
- En primer lugar, echamos en una cazuela un litro y cuarto de leche, azúcar, canela, la cáscara de naranja y la de limón. Lo ponemos al fuego y lo dejamos calentar. Cuando se ponga a cocer, le retiramos la naranja, el limón y la canela.
- Por otro lado, en un bol, mezclamos el azúcar y la maicena con ayuda de una varilla.
- En otro bol, mezclamos la leche que nos sobra con las yemas de huevo. Removemos y lo añadimos al bol del azúcar y la maicena. Mezclamos para conseguir una pasta.
- Vertemos en el bol la leche caliente y lo ponemos en otra cazuela a fuego fuerte para que la mezcle espese, durante 5 minutos sin parar de remover.
- Echamos la mezcla en una bandeja honda y lo dejamos enfriar en la nevera durante dos horas para que se solidifique.
- Cortamos la masa de la leche frita en círculos, con ayuda de un cortapastas.
- Pasamos los círculos de leche frita primero por harina y luego por huevo. Freímos en una sartén con aceite y reservamos sobre papel de cocina para evitar el exceso de grasa.
- Mientras que se fríe la leche frita, vamos a preparar el Carpaccio de naranja. Pelamos las naranjas y las cortamos en rodajas.
- En un bol, mezclamos azúcar y canela y pasamos los círculos de leche frita por ello.
- Emplatamos una base de rodajas de naranja con un chorrito de agua de azahar y la leche frita.
- Servimos.
Este fin de semana María tendrá de visita en su casa a su mamá y papá, a su hermano, a la esposa del hermano y a sus 4 sobrinos. Es decir, vendrán 8 personas de visita, que al sumarlos con los 4 miembros de la familia de María da un total de 12 personas.
María ha decidido que de postre hará leche frita. Pero ha encontrado un problema: la receta original es para 4 personas y ahora necesita prepararla para 12 personas.
Veamos cómo resolvió el problema:
Lo primero que hizo María fue considerar que si la receta inicialmente era para 4 personas, entonces al duplicar los ingredientes el postre alcanzaría parta alrededor de 8 personas.
María organizó la información en un cuadro como el siguiente:
| NÚMERO DE PERSONAS | CANTIDAD DE INGREDIENTES |
| 4 | Igual a la receta original. |
| 8 | El doble de la receta original. |
| 12 | El triple de la receta original. |
Pero duplicando la receta los ingredientes no alcanzaban para que comieran las 10 personas pues quedaban 4 personas sin poder disfrutar de la porción que le correspondería del postre. Entonces, María se dio cuenta que si triplicaba la receta original las 12 personas disfrutarían de su porción de leche frita.
María tendrá entonces que reunir, 3 VECES LA CANTIDAD DE INGREDIENTES DE LA RECETA ORIGINAL.
Vamos a ayudar a María a calcular los ingredientes:
AZÚCAR: La receta original necesita 14 kg de azúcar, veamos cuánto sería 3 veces esa medida. Para determinarla representaremos gráficamente.
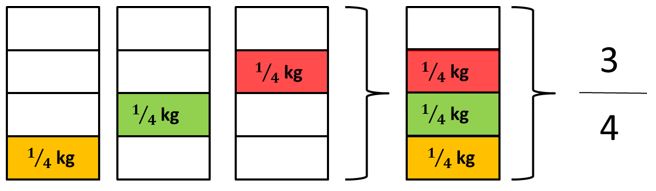
¡Entonces necesitaría 34 kg de azúcar!
Al observar con detalle la fracción de azúcar que necesita María para hacer la leche frita, nos damos cuenta que se requiere menos de 1 kilogramo de azúcar.
Como podemos ver 34 es menor que la unidad. También se puede notar que el numerador de 34 es menor que el denominador.
34 es una fracción propia
LECHE: En la receta original de María se necesita 112 l de leche.
Veamos cómo está compuesto el número 112 .
Este número está conformado por un número natural y una fracción propia, y es mayor que la unidad.
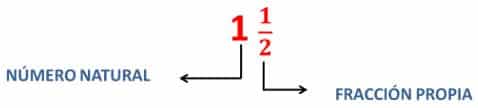
A este tipo de números se le llama Números Mixtos.
Ahora calcularemos cuánta leche se necesitan para las 12 personas.
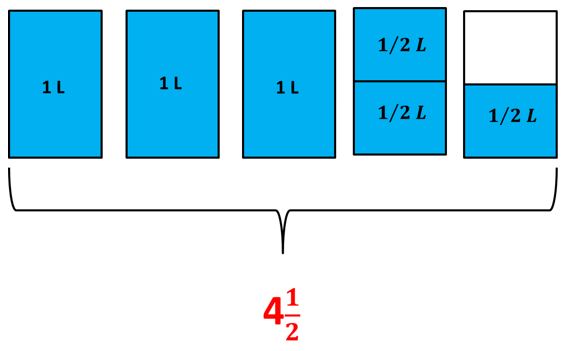
¡Entonces se necesitan 412 l de leche!
Si observamos con detenimiento vemos que en las cuatro unidades y media hay nueve medios.
Veamos:
Vamos a dividir en medios cada unidad. Dividimos la unidad en medios, pues ese es el denominador de la parte fraccionaria de nuestro número mixto 412.
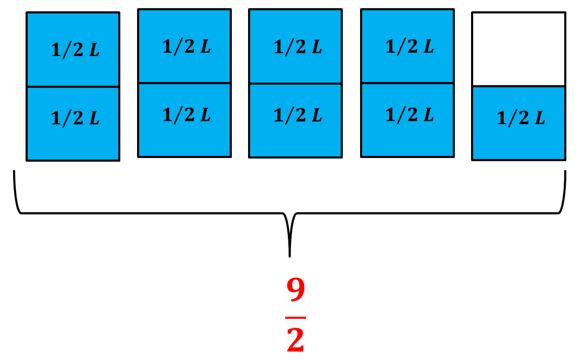
El número 412 es equivalente a la fracción impropia 92 .
La fracción 92 es impropia ya que es mayor que la unidad.
MAICENA: En la receta original de la leche frita se necesita 18 .
Para 12 personas necesitamos 3 veces 18 kg de Maicena.
Veamos:
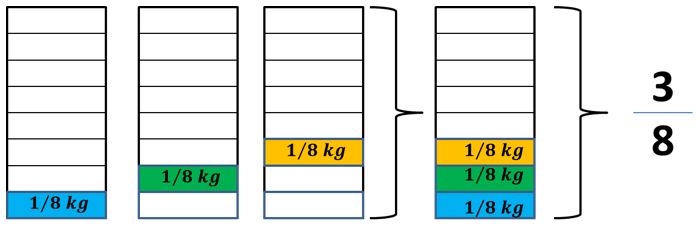
Entonces, María necesita para la receta de 12 personas 38 kg. La fracción 38 es una Fracción Propia.
HUEVO, RAMA DE CANELA, CÁSCARA DE NARANJA, LIMÓN, NARANJAS: Revisa las cantidades que se necesitan de cada uno de estos ingredientes en la receta original, que es para 4 personas. Utiliza de apoyo los cálculos que ya hemos realizado para determinar la cantidad de estos ingredientes que se necesitan para preparar la leche frita para 12 personas.
Cómo ir de un número mixto a una fracción impropia
Dado el número mixto 234 lo escribiremos como una fracción impropia.
Al representa gráficamente 234 obtenemos lo siguiente:

Fíjate que nos quedan dos unidades completas y tres cuarto de la tercera.
Si queremos, a partir de la representación gráfica, escribir el número mixto 234 como una fracción impropia, entonces contamos cuántos cuartos hay en total en 234.
La razón por la que contamos en cuartos es porque la fracción propia del número mixto 234 está denominada en cuartos.
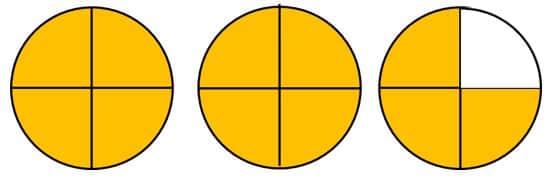
Al contar los cuartos que hay en 234 obtenemos que son once cuartos.
Entonces, 234 es equivalente a 114 .
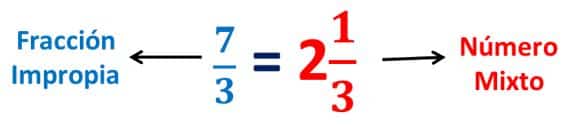
También es posible ir de un número mixto a una fracción impropia siguiendo los siguientes pasos.
- Se deja el mismo denominador de la fracción propia.
- El número natural se multiplica por el denominador y se suma el numerador.
Veamos:
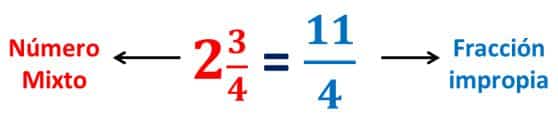
Este procedimiento siempre funciona para ir de un número mixto a una fracción impropia.
Cómo ir de una fracción impropia a un número mixto
Dada la fracción impropia 73 la escribiremos como un número mixto.
Representando gráficamente la fracción 73 obtenemos lo siguiente:
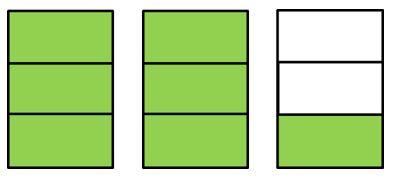
Observa que al contar nos quedan dos unidades completas y un tercio de la tercera. Esto es:

Entonces, 73 es equivalente a 213.
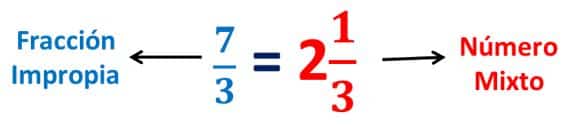
Otra manera de pasar de una fracción impropia a un número mixto es la siguiente:
- Se divide el numerador de la fracción impropia por su denominador.
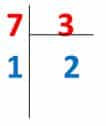
- El cociente de la división anterior se convierte en el número natural del número mixto.
- El resto de la división es el numerador de la fracción.
- El denominador de la fracción propia es el mismo que el de la fracción impropia. Este número es el divisor de la división anterior.

De esta manera se puede transformar una fracción impropia en un número mixto.
Practica con lo que hemos visto hasta ahora haciendo esta ficha:
Fracción de un número
Ya hemos visto como representar fracciones de un todo digamos continuo, como 12 de una tarta ó 75 de una pizza, etc.
Pero la fracción de un número tiene que ver con la cantidad que representa una fracción de un número dado.
Por ejemplo, cuando queremos saber cuánto es 25 de 30, o cuando nos interesa conocer cuánto es 57 de 42 lo que queremos es calcular la fracción de un número.
Para entender cómo calcular la fracción de un número vamos a trabajar con un par de ejemplos tipo problema.
Veamos:
Problema 1:
Imagina que en tu colegio hay una ley que dice lo siguiente:
“Para que sean válidas las decisiones tomadas por este curso deben ser aprobadas por dos tercios de los estudiantes.”
Si en tu clase hay 27 estudiantes, incluyéndote. ¿Cuántos votos necesitarías si quieres que se apruebe un tiempo de baile grupal cada viernes para divertirse?
¿Cómo resolverlo?
Para resolver este problema debemos recordar qué es una fracción, tal como la definimos en este artículo:
En este caso, el todo no es un pastel, ni una pizza, o un círculo.
En el caso de este problema el todo es la cantidad de estudiantes que hay en la clase. Es decir, 27 niños y niñas.

Y queremos saber cuántos estudiantes son dos tercios del todo para que puedas bailar cada viernes en clase con tus compañeros.
Es decir que la pregunta se reduce a saber cuánto es 23 de 27.
El todo entonces está dividido en 3 partes iguales, y necesitas que dos de esas partes voten por tu propuesta.
Mira cómo se vería si los colocamos en un rectángulo dividido en partes iguales:

Fíjate que hemos dividido en partes iguales el todo. Como se trata de 27 estudiantes al dividir en tres partes iguales tenemos:
27 ÷ 3 = 9
Por eso ves que en cada porción hay 9 estudiantes.
Vamos a seleccionar 2 de esas partes para saber la cantidad de niños que hay:
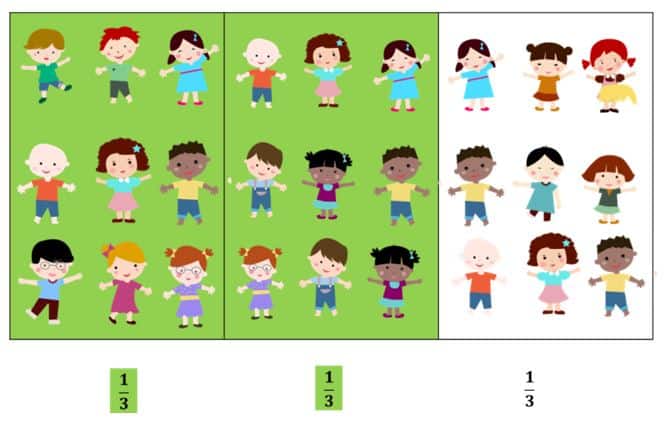
Como puedes observar estos dos tercios que están de verde corresponden a 18 estudiantes.
Podemos decir entonces que 23 de 27 es igual a 18.
Por último, concluimos que necesitas 18 votos a favor de tu propuesta para poder bailar un rato cada viernes.
Fíjate que acabamos de ver cómo podemos calcular la fracción de un número de forma gráfica. Veamos cómo hacer este procedimiento numéricamente.
Recuerda que calcularemos cuánto es 23 de 27
Lo que hacemos es dividir el número entero 27 por el 3, que es el denominador de la fracción. Así sabemos qué cantidad de estudiantes hay en cada uno de los tercios.
Luego, multiplicamos el resultado de la división por 2 que es el numerador de la fracción. Pues queremos saber qué cantidad de estudiantes hay en 2 tercios.
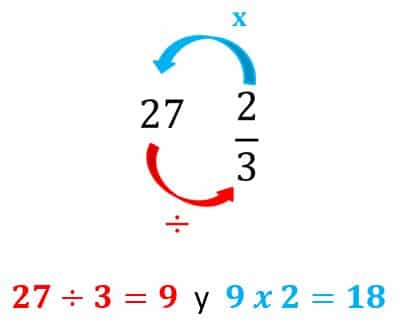
Vemos que 23 de 27 es igual a 18, por lo que necesitas 18 votos para aprobar a propuesta del baile.
Veamos otro ejemplo de fracción de un número.
Problema 2:
Los 25 de los ahorros de Daniela son 3.050 euros. ¿Cuánto dinero tiene ahorrado en total Daniela?
Solución:
Como los 25 de los ahorros de Daniela son 3.050 euros, sabemos que el total de los ahorros está dividido en 5 partes iguales:
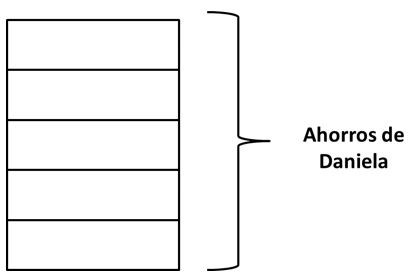
Sabemos que 2 quintos del total son 3050, entonces al dividir entre 2 sabremos cuánto hay en cada uno de esos quintos.
3.050 ÷ 2 = 1.525
Entonces 15 de los ahorros es igual a 1.525 euros.
Veámoslo gráficamente:
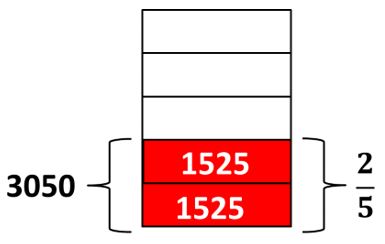
Si queremos saber el total completamos la unidad:
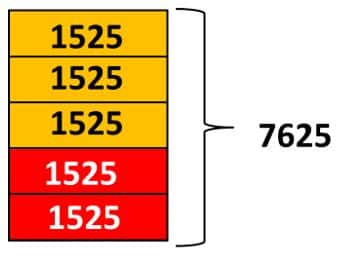
En definitiva, Daniela tiene ahorrados 7.625 euros.
Otra manera de resolver este problema es la siguiente:
Sabiendo que 15 es equivalente a 1.525, y que esta cantidad es una de las cinco partes iguales que componen los ahorros de Daniela, procedemos a realizar la siguiente operación:
5 x 1.525 = 7.625
El cinco representa las cinco partes en las han sido divididos los ahorros de Daniela, mientras el 1.525 es una de esas partes. Al multiplicar 5 por 1.525 se obtiene 7.625, que son los ahorros totales de Daniela.
Antes de dar por concluido este texto, te dejamos estas actividades para que practiques la fracción de un número.
Selecciona un juego 👇 👇 👇

Fracciones propias - impropias y número mixto 1

Pasar de fracciones a número mixto

Fracciones propias - impropias y número mixto 2

Fracciones propias - impropias y número mixto 3

Cuestionario

Fracciones propias - impropias y número mixto 1

Pasar de fracciones a número mixto

Fracciones propias - impropias y número mixto 2

Fracciones propias - impropias y número mixto 3

Cuestionario
SABER MÁS SOBRE FRACCIONES | |
| Multiplicación y división de fracciones | |
![]() Registrado en SafeCreative.
Registrado en SafeCreative.