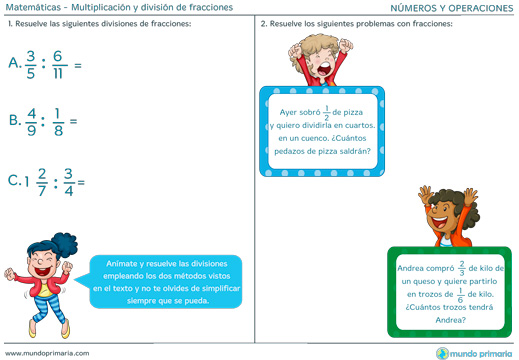
Multiplicación y división de fracciones
A lo largo de este artículo explicaremos ampliamente cómo multiplicar y dividir fracciones. Utilizaremos varios métodos para ello y también realizaremos las representaciones gráficas oportunas para comprenderlo mejor. Completaremos el artículo con varios problemas detalladamente explicados.
- Echa un vistazo: Los números romanos.
Multiplicación de fracciones
La multiplicación de fracciones es una de las operaciones fundamentales en este tipo de números. Y además es una de las más sencillas. Para multiplicar dos fracciones se procede así:
1. Obtienes el producto de los numeradores, que será el numerador de la fracción resultante.
2. Calculas el producto de los denominadores, que es el denominador de la fracción que resulta de esta operación.
En el siguiente ejemplo obtendremos el producto de estas dos fracciones:
35 x 47
Para resolver esta multiplicación de fracciones procedemos de la siguiente manera:
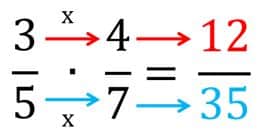
Fíjate que multiplicamos los numeradores para obtener 12, el numerador del resultado. También multiplicamos los denominadores y obtuvimos 35, que es el denominador de la fracción resultante.
Representación gráfica de la multiplicación de fracciones
La multiplicación de fracciones también puede ser representada de forma gráfica.
En este caso seguiremos con nuestro ejemplo 35 x 47. Veamos:
- Se representan cada una de las fracciones en unidades separadas y de igual tamaño:
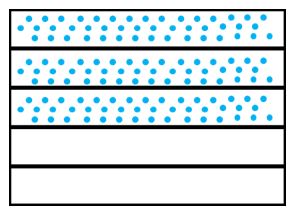 | 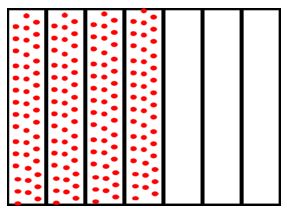 |
| 35 | 47 |
Fíjate que los 35 los hemos representado con puntitos azules y los 47 los representamos con puntitos rojos.
- Superponemos ambas representaciones para obtener la región en la que coinciden (o se intersectan) ambas gráficas.
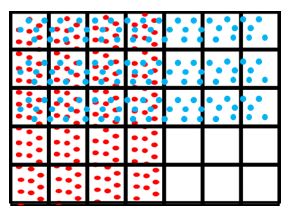
Debes considerar lo siguiente:
- La nueva unidad quedó dividida en 35 partes iguales. Entonces 35 es nuestro nuevo denominador.
- Los puntitos rojos y los puntitos azules coinciden en 12 de estas 35 partes. Por lo que 12 es el nuevo numerador.
- La fracción resultante es:
1235
Como puedes observar, el resultado del método gráfico es igual al del método analítico, que describimos al principio.
Otros ejemplos de multiplicación de fracciones
Observa detenidamente estos ejemplos resueltos de multiplicación de fracciones que te presentamos a continuación. Te ayudarán a tener una mayor comprensión del tema y te permitirán aplicar el procedimiento de forma más rápida.
Además, repasaras algunas cosas más sobre las fracciones que podrás encontrar en otros textos publicados cuyos enlaces encontrarás al final de este texto.
- Ejemplo 1: (Fracción por número entero)
- Hallar el producto 4 x53
- Como sabemos que 4=41 podemos reescribir la multiplicación así:
- Hallar el producto 4 x53
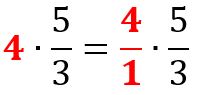
- Ahora operamos como ya sabemos hacerlo:
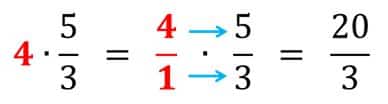
- Ejemplo 2: (Simplificación de uno de los factores)
- Multiplicar 1215x254
- En este caso, antes de realizar la multiplicación vamos a simplificar el primer factor.
- Es decir, simplificamos 1215.
- Como podemos ver, 12 y 15 son múltiplos de 3, por lo que dividimos entre 3 tanto el numerador como el denominador.
- Multiplicar 1215x254
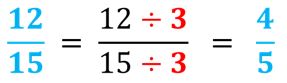
- Ahora que tenemos la fracción simplificada podemos reescribir la multiplicación, nos quedaría así:
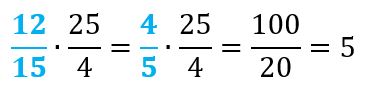
- En este caso el resultado fue simplificado, ya que el numerador es divisible entre el denominador lo que hicimos fue encontrar ese cociente.
- Ejemplo 3: (Simplificación del resultado)
- Multiplica las siguientes fracciones 185x19
- En este caso no es posible simplificar ninguna de las dos fracciones, entonces procedemos a multiplicar directamente:
- 185x19=1845
- Este resultado también puede simplificarse. Si observas te das cuenta que 18 y 45 son múltiplos de 9. Entonces nos queda:
- 1845=18÷945÷9=25
- En este caso no es posible simplificar ninguna de las dos fracciones, entonces procedemos a multiplicar directamente:
- Multiplica las siguientes fracciones 185x19
- Ejemplo 4: (simplificación de los factores y del producto)
- Resuelve el siguiente producto 1215x2636
- En este caso empezamos simplificando ambos factores.
- Resuelve el siguiente producto 1215x2636

- Ahora reescribimos la multiplicación, quedándonos así:
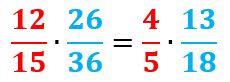
- Y resolvemos normalmente:
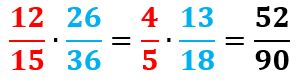
- Por último, simplificamos el resultado. Como ambos son múltiplos de 2 nos queda:
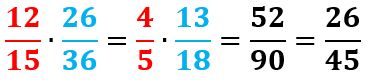
- Ejemplo 5: (Multiplicación de más de dos fracciones)
- Calcula el producto de 47x18x25
- En este caso realizamos la multiplicación directa de los numeradores, para obtener el nuevo numerador, y de los denominadores, para obtener el nuevo denominador.
- Calcula el producto de 47x18x25

- Ahora simplificamos el resultado. En este ejemplo tanto el numerador como el denominador son múltiplo de 2. Nos queda entonces así:
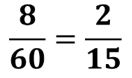
- Entonces el producto queda así:
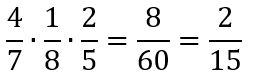
- Ejemplo 6: (Multiplicación de números mixtos)
- Resuelve la siguiente multiplicación: 212x43
- Aquí debemos expresar el número mixto en forma de fracción, es decir 212 pasará a ser una fracción impropia.
- Para ello operamos de la siguiente manera: Tomamos como denominador de la fracción impropia el mismo que tiene la fracción del número mixto, que en este caso es 2.
- Resuelve la siguiente multiplicación: 212x43
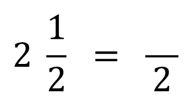
- Para conseguir el numerador multiplicamos la parte entera del número mixto por el denominador de la fracción del número mixto, luego sumamos el numerador de esa fracción. En este caso (2×2)+1=5.
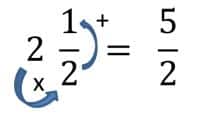
- Ahora reescribimos el producto y lo resolvemos como de costumbre.
212x43=52x43=206
- Este resultado lo podemos simplificar porque tanto 20 como 6 son múltiplos de 2:
206=103
- El producto nos queda:
212x43=103
Problemas con multiplicación de fracciones
- Problema 1:
- Una receta para pastelillos de plátano y avena necesita 34 de taza de avena. Vamos a preparar la mitad de la receta. ¿Cuánta avena necesitaremos?
- Solución:
- En este caso multiplicamos las 34 de taza de la receta original por el 12 que representa la mitad de la receta.
- 12x34=38
- Entonces para preparar la mitad de la receta necesitamos 38 de taza de avena.
- En este caso multiplicamos las 34 de taza de la receta original por el 12 que representa la mitad de la receta.
- Problema 2:
- Javier vende huevos que vienen en cartones por docena. María, que es cliente frecuente de su tienda, le pide solamente 56 de docena y Javier accede a vendérselos, ¿cuántos huevos debe venderle Javier a María?
- Solución:
- En este caso encontraremos los 56 de los 12 huevos, pues una docena es igual a 12.
- Este problema puede resolverse de forma gráfica y empleando la multiplicación de fracciones. Apliquemos primero la multiplicación.
| OPERACIÓN | EXPLICACIÓN |
| 56x12=56x121 | Reescribiendo 12=121. |
| 56x12=5×126×1 | Multiplicamos los numeradores de ambas fracciones. Multiplicamos los denominadores de ambas fracciones. |
| 56x12=606 | Obteniendo el producto del numerador y del denominador. |
| 56x12=10 | Simplificando el resultado al dividir numerador entre el denominador. |
- Por último, Javier debe venderle 10 huevos a María.
- Veamos cómo resolver este problema de manera gráfica:
- Recordemos que María quiere 56 de la docena de huevos. Por eso primero dividimos la docena de huevos en 6 partes iguales.
- Veamos cómo resolver este problema de manera gráfica:
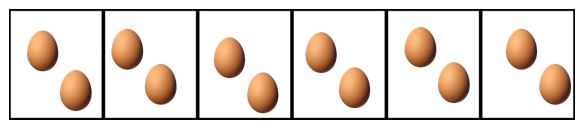
- Ahora tomamos 5 de esas partes, es decir seleccionamos los 56 de la docena.

- Al contar cuántos huevos hay en estos “cinco sextos” podemos ver que hay 10 huevos.
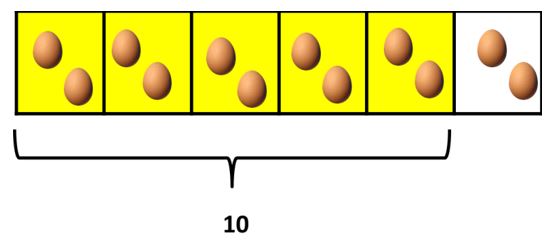
- De manera que Javier debe venderle 10 huevos a María.
- Problema 3:
- Raquel estuvo 112 horas en la playa. Ese día se quedó dormida y pasó 34 de ese tiempo bajó el sol, y luego despertó con la piel muy bronceada. ¿Cuántas horas pasó Raquel dormida en la playa?
- Lo que queremos es saber cuánto es 34 de 112 , y para eso debemos multiplicar ambos números.
- Es decir que resolveremos 34x 112
- Entonces, lo primero que haremos es pasar el número mixto a fracción impropia.
- Raquel estuvo 112 horas en la playa. Ese día se quedó dormida y pasó 34 de ese tiempo bajó el sol, y luego despertó con la piel muy bronceada. ¿Cuántas horas pasó Raquel dormida en la playa?
| OPERACIÓN | EXPLICACIÓN |
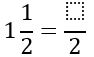 | Colocamos el mismo denominador de la parte fraccionaria del número mixto. |
| 112=(1×2)+12=32 | Multiplicamos la parte entera del número mixto por el denominador. Le sumamos el producto anterior al numerador. |
- Ahora reescribimos la multiplicación que queremos resolver:
34x112 =34 x32
- Y multiplicamos como ya sabemos hacerlo:
34x32 =98
- Por último, podemos decir que Raquel pasó 98 de hora dormida en la playa.
División de fracciones
La división de fracciones es una operación muy importante dentro de la matemática. En este artículo te enseñaremos dos métodos para dividir fracciones de tal modo que utilices el que te parezca más sencillo.
Método 1 para dividir fracciones
Para dividir dos fracciones procedemos de la siguiente manera:
1. Invertimos la segunda fracción. Esto es, el numerador de esta fracción pasa a ser su denominador y el denominador se convierte en su nuevo numerador.
2. Simplificamos hasta la mínima expresión.
3. Obtenemos el producto de los numeradores, que será el numerador de la fracción resultante.
4. Calculamos el producto de los denominadores, que es el denominador de la fracción que resulta de esta operación.
- Veamos un ejemplo:
Dividiremos 65 entre 910. Es decir, 65÷910 .

Hemos visto que para dividir dos fracciones procedemos a invertir la segunda fracción y luego hacemos la multiplicación correspondiente.
Veamos otra manera de realizar la división de fracciones.
Método 2 para dividir fracciones
Para dividir dos fracciones realizamos lo siguiente:
1. Multiplicamos el numerador de la primera fracción por el denominador de la segunda fracción. El resultado lo escribimos en el numerador de la nueva fracción.
2. Multiplicamos el denominador de la primera fracción por el numerador de la segunda fracción. El resultado es el nuevo denominador.
3. Simplificamos la fracción resultante, de ser posible.
- Veamos un ejemplo con este método:
Dividiremos 37÷114 . Esto es:

Entonces el resultado de dividir 37÷114 es 1277.
Como te has podido dar cuenta dividir fracciones es muy sencillo. ¡Prueba superada!
Representación gráfica de la división de fracciones
Antes de representar la división de fracciones vamos a recordar uno de los significados de la división de dos números naturales.
Por ejemplo, si queremos calcular el cociente que resulta de dividir 14 ÷ 4 , entonces nos preguntamos cuántas veces está contenido 4 en 14.
Para visualizar cuántas veces está 4 en 14, representaremos esta operación en la recta numérica. Veamos:
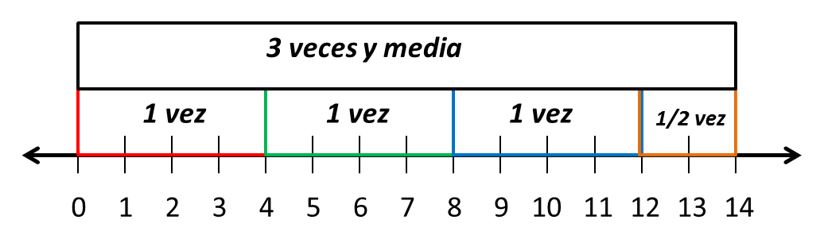
En la gráfica se observa que 4 está contenido 3 veces y media en 14.
También podemos dividir 14 ÷ 4 para determinar cuántas veces está contenido 4 en 14. Esto es:
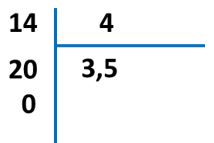
El cociente de esta división indica que 4 está contenido 3,5 veces en 14.
Ahora aplicaremos este mismo principio de la división como contención, para analizar la representación gráfica de la división de fracciones.
- Realicemos gráficamente la siguiente división 34÷12 .
- En este ejemplo veremos cuántas veces está contenido12en34.
- Primero representamos gráficamente las fracciones de la división.
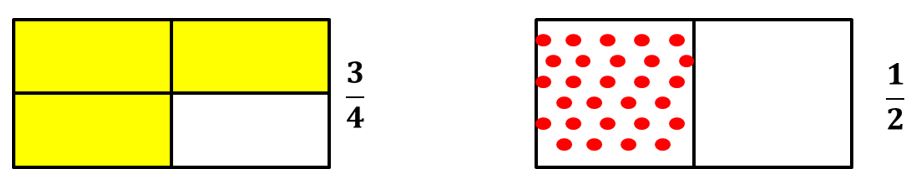
- Ahora superponemos 12en34
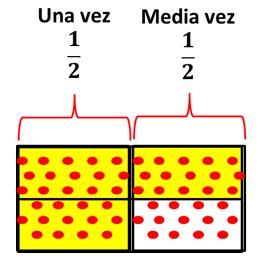
- En la representación gráfica se observa que 12 está contenido una vez y media en 34. Entonces, 34÷12= 112 .
- También, se puede decir que 34÷12=3×24×1 =64 =32 =112
- Resolvamos gráficamente la división 13÷13. En este caso también utilizaremos la idea de contención para interpretar la representación gráfica y obtener el cociente de esta división.
- Lo primero que hacemos es representar gráficamente las fracciones de la división.
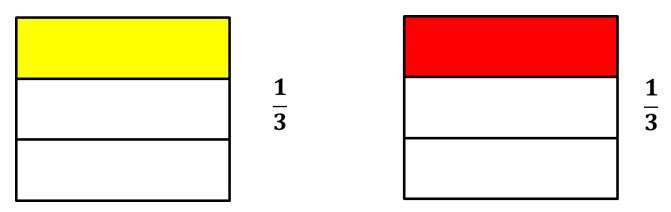
- Ahora superponemos 13en13. Veamos:
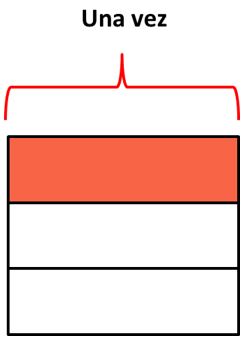
- A partir de la gráfica se observa que un tercio está contenido exactamente una vez en un tercio. Por esta razón el resultado de dividir 13÷13 es 1. Al hacerlo analíticamente se tiene que:
13÷13=1×31×3=33=1
- Problema 1:
- María desea empaquetar 812 kg de azúcar en bolsas de 14kg. ¿Cuántas bolsa de 14kg se pueden llenar con todo este azúcar?
- Solución:
- Para reconocer que este problema se puede resolver con una división de fracciones, es muy importante la idea de contención que estudiamos antes. Esto debido a que en este caso debemos determinar cuántas veces está contenido 14en 812.
- Primero transformamos el número mixto812en su fracción impropia equivalente. Veamos:
| OPERACIÓN | EXPLICACIÓN |
| 812=172 | Se multiplica el número 8 por el denominador de la fracción propia que en este caso es 2. 8 . 2 = 16, a este resultado le sumamos el número 1 ubicado en el numerador de la fracción propia 16 + 1 = 17. El 17 es el numerador de la fracción impropia que estamos buscando y el denominador es el mismo 2. |
- Ahora como debemos establecer cuántas veces está contenida la fracción 34en172, procedemos a efectuar la división 172÷34.
| OPERACIÓN | EXPLICACIÓN |
| 172÷14=172x41 | Invertimos la segunda fracción. El numerador pasó a ser el denominador y el denominador se convirtió en el numerador. |
| 172÷14=17×42×1 | Multiplicamos linealmente. Numerador con numerador y denominador con denominador. |
| 172÷41=682 | Resolviendo las multiplicaciones anteriores. |
| 172÷41=341= 34 | Simplificamos la fracción, dividiendo el numerador y el denominador entre 2. |
- Entonces, con los 812kg de azúcar se pueden llenar 34 bolsas de 14kg.
- Problema 2:
- Sofía pinta estatuas. Le quedan 54de litro de pintura. Cada estatua requiere 120de litro de pintura. ¿Cuántas estatuas puede pintar con la pintura que le queda?
- Solución:
- Nos fijamos que nuevamente debemos ver cuántas veces está contendida una de las fracciones en la otra, para dar respuesta a la pregunta del problema. Esta estructura es muy común en los problemas de división. En este caso vamos a calcular cuántas veces54contiene120. Esto es:54÷120
| OPERACIÓN | EXPLICACIÓN |
| 54÷120=5×204×1 |
|
| 54÷120=1004=251=25 | Simplificamos la fracción, dividiendo el numerador y el denominador por 4. |
- De esta manera obtenemos que con los54de litro de pintura se pueden pintar 25 estatuas.
Selecciona un juego 👇 👇 👇

Multiplicación de fracciones 1

Multiplicación de fracciones 2

División de fracciones 1

División de fracciones 2

Cuestionario

Multiplicación de fracciones 1

Multiplicación de fracciones 2

División de fracciones 1

División de fracciones 2

Cuestionario
SABER MÁS SOBRE FRACCIONES | |
| Suma y resta de fracciones | |
![]() Registrado en SafeCreative.
Registrado en SafeCreative.