Fracciones
¿Te apetece poner a prueba todo lo que sabes de fracciones antes de leer el artículo? Te proponemos este cuestionario para hacerlo y no te preocupes si no sale como esperas, siempre puedes volver a hacerlo una vez hayas finalizado la lectura.
¿Qué es una fracción?
Para comprender qué son las fracciones vamos a empezar con un ejemplo.
La mamá de Pablo ha preparado una deliciosa lasaña de carne para un almuerzo especial, tal como ves en esta imagen:

Los comensales invitados a este almuerzo son 8, incluyéndola, así que la mamá de Pablo repartirá la lasaña en 8 partes iguales. Veamos:

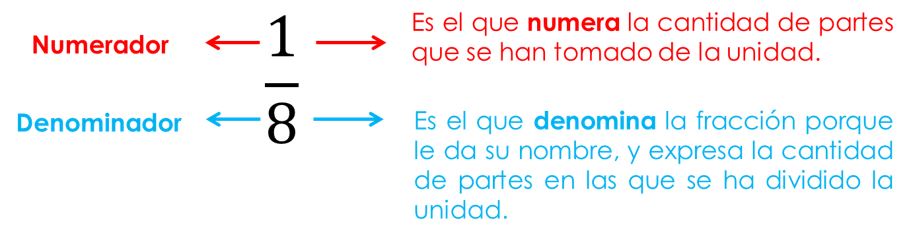
A cada comensal le tocará una porción igual de la lasaña. En este caso, a cada comensal le tocará 1 de las 8 partes iguales en las que se ha dividido la lasaña.
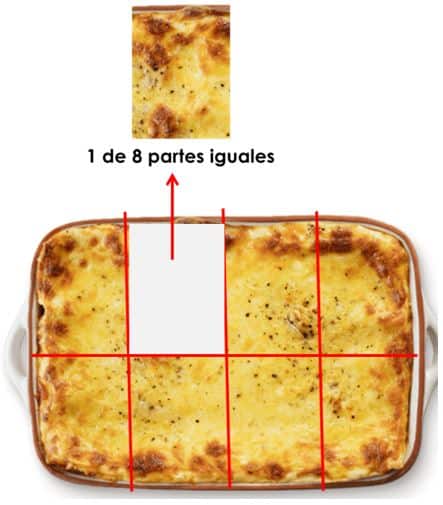
Cada una de esas partes representa una fracción de la lasaña.
Para entender qué es el numerador y qué es el denominador de una fracción volvemos a nuestro ejemplo de la lasaña.
Observa:
| 1 DE 8 PARTES IGUALES | REPRESENTACIÓN: |
 | Cada trozo de lasaña se representa con esta fracción: 18 |
Nombres de las fracciones
Sigamos con nuestro ejemplo para saber cómo se van llamando las fracciones:
En el almuerzo que organizó la mamá de Pablo participaron sólo 6 de las 8 personas que estaban previstas, porque a Carlitos y a su mamá se les presentó un inconveniente y no pudieron asistir.
A continuación te presentamos cómo quedó la bandeja de la lasaña, luego de repartir una porción a cada una de las 6 personas presentes en el almuerzo.

Podemos afirmar varias cosas a partir de esta imagen de la bandeja de lasaña:
- No se comieron 2 de los 8 pedazos de la lasaña. La fracción que representa los pedazos que no se comieron es esta:
28
Podemos decir que quedaron “dos octavos” de la lasaña.
- Se comieron 6 de los 8 pedazos de la lasaña. La porción que se comieron de la lasaña quedaría en fracción así:
68
Podemos decir que quedaron “seis octavos” de la lasaña.
Nombres de fracciones según su denominador
Observa cómo se denomina cada fracción de acuerdo con el número que tenga en el denominador.
| DENOMINADOR | NOMBRE DE LA FRACCIÓN: |
| 2 | Medios |
| 3 | Tercios |
| 4 | Cuartos |
| 5 | Quintos |
| 6 | Sextos |
| 7 | Séptimos |
| 8 | Octavos |
| 9 | Novenos |
| 10 | Décimos o décimas |
| 11 | Onceavos |
| 12 | Doceavos |
| 13 | Treceavos |
| 100 | Centésimos o centésimas |
| 1.000 | Milésimos o milésimas |
| 10.000 | Diezmilésimos o diezmilésimas |
| 100.000 | Cienmilésimos o cienmilésimas |
| 1.000.000 | Millonésimos o millonésimas |
Como puedes notar, después del denominador 10 las fracciones toman el nombre del número correspondiente y se le añade el sufijo “avos”.
De manera que, por ejemplo, si el denominador de la fracción es 23 la fracción se denominaría “veintitresavos”.
Veamos estos ejemplos de nombres de fracciones:
| FRACCIÓN | CÓMO SE LEE: |
59 | Cinco novenos |
711 | Siete onceavos |
43 | Cuatro tercios |
732 | Siete treinta y dosavos |
1155 | Once cincuenta y cincoavos |
710 | Siete décimos o siete décimas |
31.000 | Tres milésimas |
171.000.000 | Diecisiete millonésimas |
Representación gráfica de las fracciones
Imagina que tu mamá trae una caja con una tarta de limón a casa, pero antes de que puedas abrirla te advierte que de las 6 porciones iguales que traía la tarta, le regaló 2 porciones a su vecina, una para ella y otra para su hijo.
Esto lo podemos representar gráficamente de la siguiente manera:
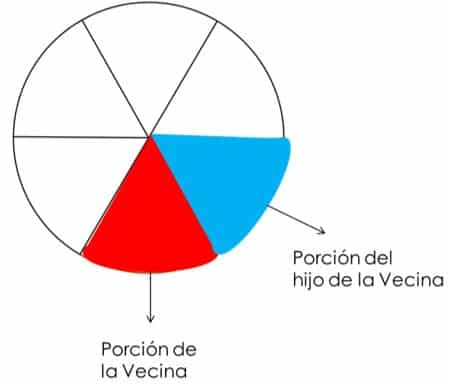
De esta situación podemos ver lo siguiente:
- La parte blanca del gráfico representa 46 (cuatro sextos) del pastel de limón, y esa es la cantidad de tarta que quedó para repartir en tu casa.
- Las partes azul y roja juntas representan 26 (dos sextos) de la tarta, que fue la parte que tu mamá regaló a la vecina y a su hijo.
- La parte azul corresponde a 16 (un sexto) del pastel, que es la parte que se comerá el hijo de la vecina. Y que además es igual a la fracción del pastel que se comerá su madre, representada por la parte roja.
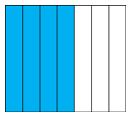
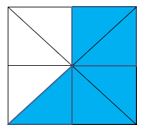
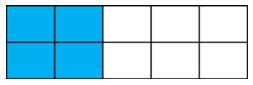
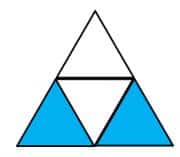
Veamos otras representaciones de fracciones:
En cada caso representamos la porción coloreada de azul.
| REPRESENTACIÓN GRÁFICA | FRACCIÓN EN NÚMEROS |
| 47 |
| 58 |
| 25 (Fijándonos solo en las divisiones verticales) 410 (Fijándonos en todas las divisiones) |
| 24 |
| 56 |
Las fracciones en la vida cotidiana
Veamos ahora diferentes ejemplos que utilizamos de manera normal en nuestra vida diaria.
Ejemplo 1: El agua que tomamos
| EL AGUA QUE TOMAMOS | |
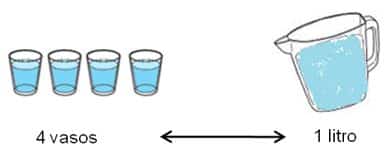
| Vamos a suponer que debemos compartir en partes iguales, y sin que sobre nada, un litro de agua en cuatro vasos de los que se usan regularmente para consumir el vital líquido. |
Al repartir todo el litro de agua en cuatro partes iguales. Tenemos que cada vaso representa una de las cuatro partes en la que ha quedado dividido el litro de agua. Entonces, un vaso equivale a un cuarto de litro, aproximadamente. | 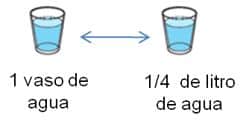 |
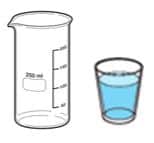
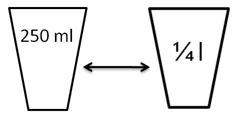
| Si tomamos la cantidad de agua que hay en uno de los vasos de la actividad anterior y la colocamos en una probeta o en un vaso graduado, determinaremos que un 1/4 l de agua equivale a 250 ml de agua, aproximadamente. |
 | |
Ahora veamos algunas equivalencias completando la siguiente tabla:
TABLA DE EQUIVALENCIAS | |
LITROS (l) | MILILITROS (ml) |
| 14 | 200 |
| 12 | 500 |
| 34 | 750 |
1 | 1.000 |
1510=1,5 | 1.500 |
2 | 2.000 |
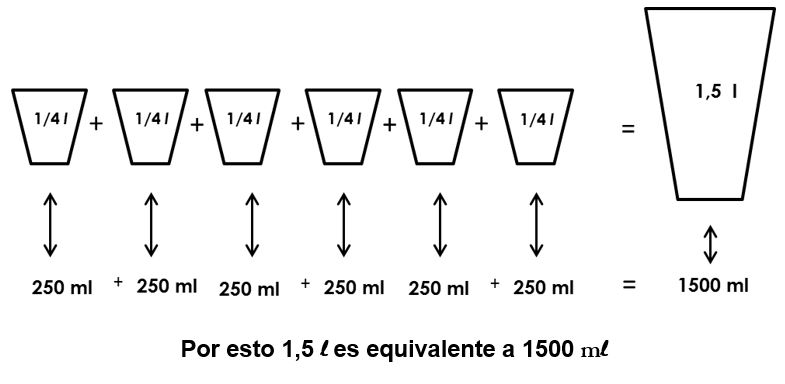
Observa cómo podemos hacerlo en el caso de un litro y medio o 1,5 litros:
- Tomamos una botella con capacidad de un litro y medio llena de agua, y vamos vertiendo el contenido de la botella en los vasos que usamos regularmente en casa.
- Sabemos que cada vaso representa un cuarto de litro de agua y, además, cada cuarto de litro es equivalente a 250 ml.
- Si sumamos el contenido de cada vaso tenemos:
Ejemplo 2: El azúcar del pastel de mi mamá
A todos nos gusta un rico pastel para merendar, cada mamá o abuelita tiene su receta. A continuación te presentamos una que queda muy rica.
Receta de ponqué de vainilla
- 250 gramos de mantequilla
- 400 gramos de azúcar
- 5 huevos.
- 500 gramos de harina de trigo
- 1 taza de leche
- 1 cucharadita de ralladura de limón
- 1 cucharadita de esencia de vainilla.
La receta dice que se necesitan 400 gramos de azúcar. Veamos que significa esta medida.
Como ejercicio vamos a repartir en cinco partes iguales, y sin que sobre nada, un kilogramo de azúcar.
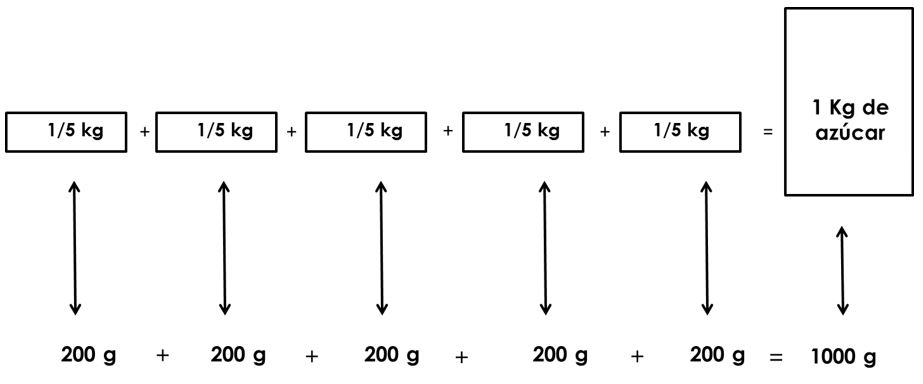
Al compartir todo el kilogramo de azúcar en cinco partes iguales, nos queda que cada recipiente representa una de las cinco partes en la que ha quedado dividido el kilogramo de azúcar.
Entonces, cada parte equivale a un quinto de kilogramo.
Cada quinto de kilogramo equivale a 200 gramos. Esto se puede verificar utilizando una balanza.
Para practicar un poco y así comprender mejor la idea de la fracción de azúcar para el ponqué, presentamos algunas equivalencias en la siguiente tabla:
TABLA DE EQUIVALENCIAS | |
KILOGRAMOS (kg) | GRAMOS (g) |
| 15 | 250 |
¿? | 400 |
| 35 | 600 |
1 | 1.000 |
1,5 | 1.500 |
2 | 2.000 |
Fíjate cómo se hace en el caso de los 400 gramos de azúcar.
- Sabemos que cada parte representa un quinto de kilogramo de azúcar y, además, que cada quinto de kilogramo es equivalente a 200 gramos.
- Si juntamos dos veces 15 kg , tal y como se observa en la figura, obtenemos que 400 gramos equivalen a 25 kg.
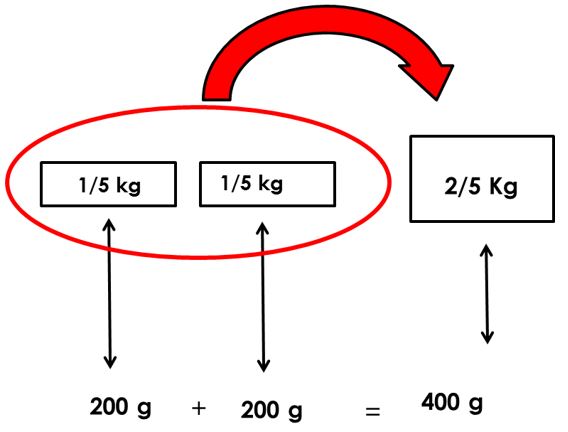
- Entonces, 25 kg equivale a 400 gramos.
Ejemplo 3: La granja de Pedro
La granja de Pedro tiene 616 en cultivos y 416 en cobertizos para gallinas. Para tener una mejor idea de cómo está distribuido el terreno representaremos gráficamente la parte de cultivos y la parte de los cobertizos.
Como las fracciones que hacen referencia al cultivo y a las gallinas tienen como denominador el 16, entonces dividiremos la unidad en 16 partes iguales.
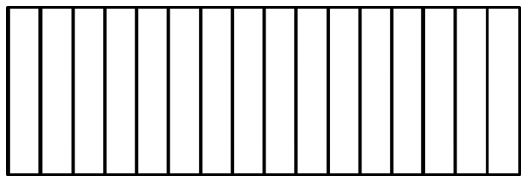
Luego, el área del cultivo la pintaremos de color rojo. Mientras que para los galpones utilizaremos el color verde.
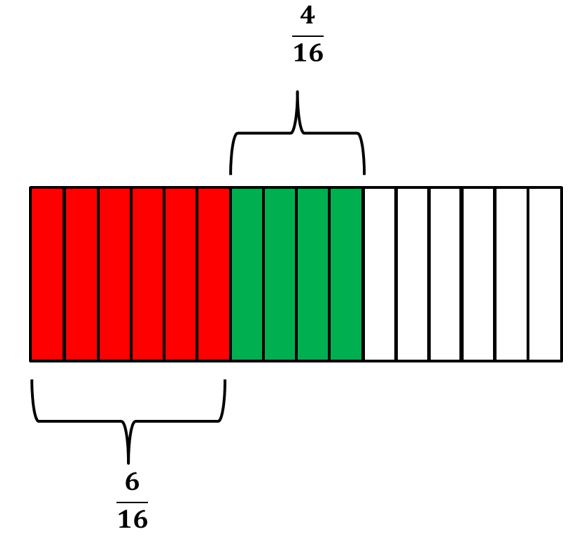
La parte de color rojo representa 616 en cultivos y la de verde los 416 en cobertizos para gallinas.
Ejemplo 4: Repartiendo el pastel
Ana debe repartir dos pasteles entre ella y sus dos hijas. Es decir, se deben repartir 2 pasteles entre tres personas, de tal manera que no sobre nada y que a cada quien le toque la misma cantidad.
¿Qué fracción de pastel le toca a cada persona?
Veamos:
En principio representaremos los pasteles en rectángulos, como se observa en la siguiente figura.
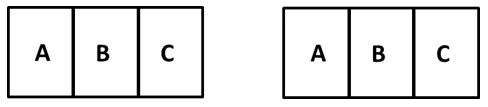
Como son 2 pasteles para 3 personas haremos la siguiente repartición.
A cada persona la hemos identificado con una letra de la siguiente manera:
La letra A se refiere a la mamá, y las letras B y C a sus hijas.
Fíjate que a cada persona le corresponde 13 del primer pastel y 13 del segundo pastel.
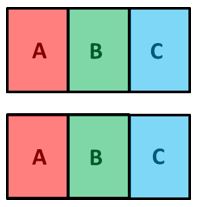
Tal y como se observa en la presentación anterior, a cada persona le corresponden 23 de pastel.
Te dejamos unas actividades para que puedas practicar lo aprendido:
Selecciona un juego 👇 👇 👇

Concepto - lectura y escritura 1

Concepto - lectura y escritura 2

Concepto - lectura y escritura 3

Cuestionario
También te pueden interesar estos temas de Matemáticas

Concepto - lectura y escritura 1

Concepto - lectura y escritura 2

Concepto - lectura y escritura 3

Cuestionario
También te pueden interesar estos temas de Matemáticas
![]() Registrado en SafeCreative.
Registrado en SafeCreative.