Cuadriláteros

Los cuadriláteros son figuras muy importantes en la geometría y es posible que tengas algunas interrogantes sobre ellos: qué son cuadriláteros, cómo se clasifican, qué ejemplos hay de cuadriláteros y cómo se construyen los distintos tipos de cuadriláteros.

Todos los estudiantes de primaria y secundaria deberían saber sobre estos polígonos de cuatro lados, y en este artículo te ayudaremos a aprender todo lo que necesitas conocer acerca de estas variadas e interesantes figuras geométricas.

 

¿Qué quiere decir la palabra cuadrilátero?

Vamos a empezar con la etimología de la palabra, es decir, qué significa cuadrilátero.

• En latín cuadrilátero se escribe quiadrilaterus, y las raíces de esta palabra son:
• Quadri que significa cuatro en latín, y lateris que significa lado.

Elementos de los cuadriláteros

Los cuadriláteros tienen, como ya dijimos, cuatro lados, pero también tienen otros elementos que los componen y caracterizan. Los cuadriláteros poseen:

1. Cuatro vértices.

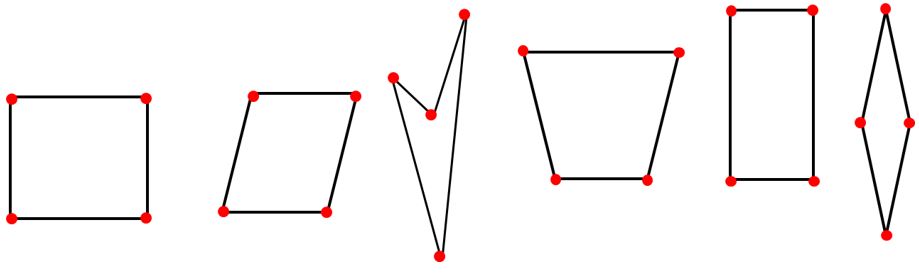
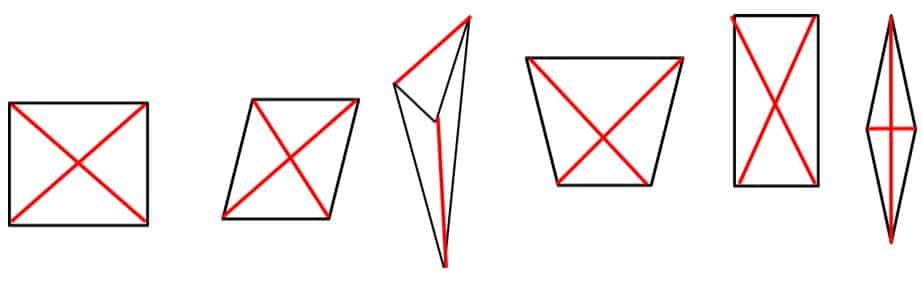
2. Dos diagonales.

3. Cuatro ángulos.

 

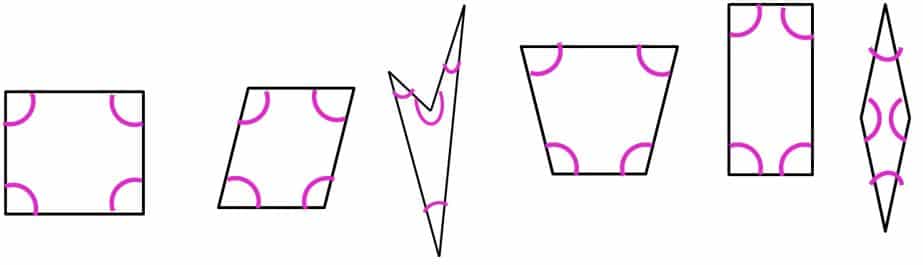
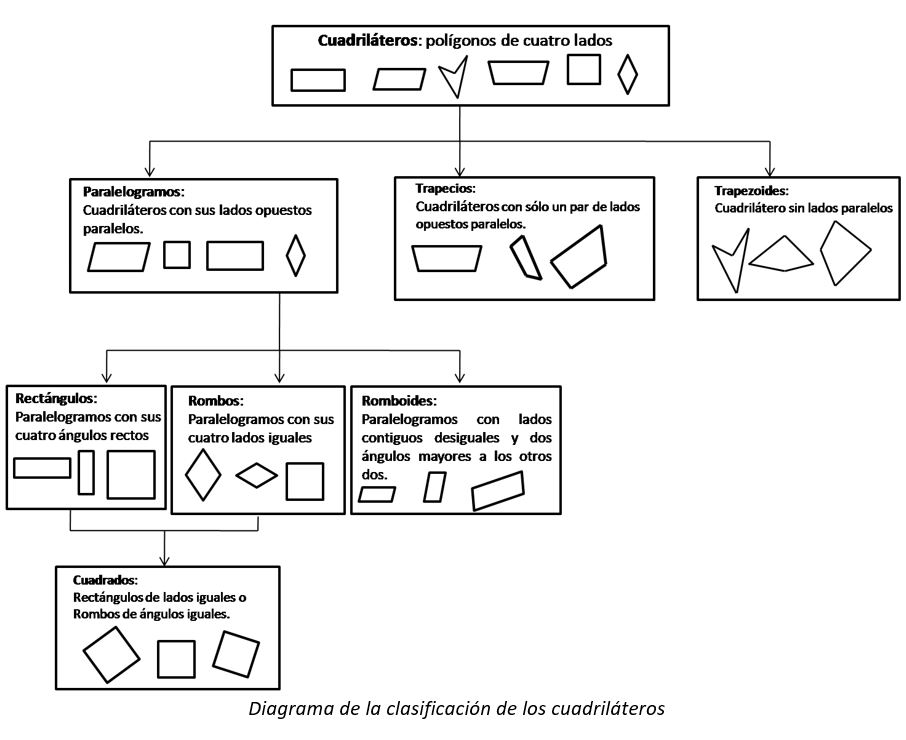
¿Cómo se clasifican los cuadriláteros?

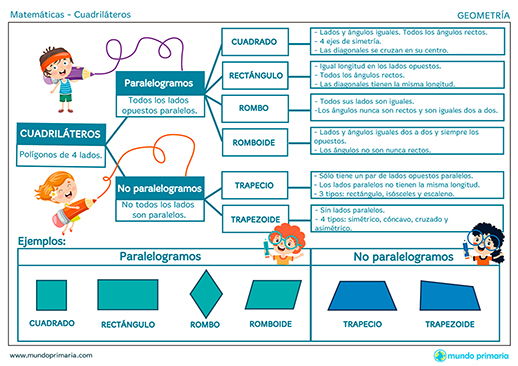
Los cuadriláteros se clasifican de acuerdo al paralelismo de sus lados en tres grandes grupos:

1. Paralelogramos: Son cuadriláteros que tienen sus lados opuestos paralelos.

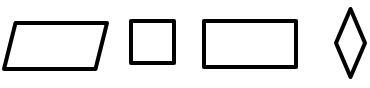
2. Trapecios: Son cuadriláteros con un único par de lados opuestos paralelos.

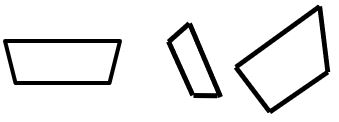
3. Trapezoides: Son cuadriláteros sin lados paralelos.

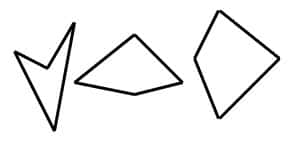
Fíjate en este diagrama que explica la clasificación de los cuadriláteros:

 

 

¿Cómo se clasifican los paralelogramos?

Como puedes observar en el diagrama, los paralelogramos se clasifican en:

1. Rectángulos: Son paralelogramos con sus cuatro ángulos rectos.

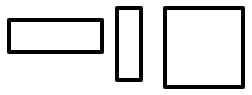
2. Rombos: Son paralelogramos con sus cuatro lados iguales.

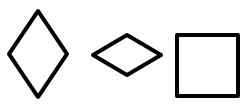
3. Romboides: Son paralelogramos con lados contiguos desiguales, dos ángulos obtusos y dos ángulos agudos.

Actividades con cuadriláteros

Lee cada uno de estos enunciados y decide si es verdadero o falso lo que indica:

• Un trapecio es un paralelogramo.
  • Falso. Los trapecios tienen solo un par de lados opuestos paralelos, mientras que los paralelogramos tienen sus dos pares de lados opuestos paralelos.
• Un cuadrado es un trapecio.
  • Falso. Los cuadrados tienen sus cuatro lados iguales y paralelos dos a dos. Los trapecios tienen un único par de lados paralelos.
• Un rectángulo es un paralelogramo.
  • Verdadero. Los rectángulos tienen sus lados opuestos paralelos, por eso son paralelogramos.
• Un cuadrado es un rectángulo.
  • Verdadero. Una de las características de los cuadrados es que sus lados opuestos son paralelos, al igual que los rectángulos, y que todos sus ángulos son rectos.
• Un paralelogramo es un rombo.
  • Falso. Los rombos son paralelogramos con todos sus lados iguales, pero no todos los paralelogramos tienen sus lados iguales. Un ejemplo de ello es el rectángulo, cuyos lados iguales son solo los opuestos.
• Un rombo es un cuadrado.
  • Falso. Aunque los rombos y los cuadrados tienen los cuatro lados iguales, solo los cuadrados tienen todos los ángulos rectos.
• Un cuadrado es un rombo.
  • Cierto. La definición de rombo es “cuadrilátero con sus cuatro lados iguales”, y esa condición la cumple el cuadrado.
• Algunos cuadriláteros son cuadrados.
  • Cierto. Entre los cuadriláteros hay cuadrados, rectángulos, trapecios, trapezoides, y paralelogramos.
• Algunos paralelogramos son rombos.
  • Cierto. Entre los paralelogramos encontramos los rombos, también los rectángulos y los romboides.
• Algunos cuadriláteros son paralelogramos.
  • Cierto. Además de los paralelogramos, los cuadriláteros se clasifican en Trapecios y trapezoides.

 

¿Qué son los cuadrados?

Estas dos características los hacen cuadriláteros muy especiales porque son rectángulos y rombos a la vez.

Veamos distintas formas de representar los cuadrados en la cuadrícula de puntos:

 

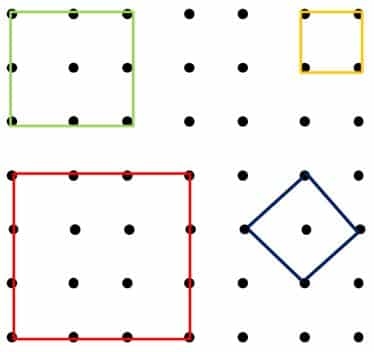
Como puedes observar cada uno de los cuadrados tiene los cuatro lados iguales y los cuatro ángulos rectos.

 

Propiedades de los cuadrados

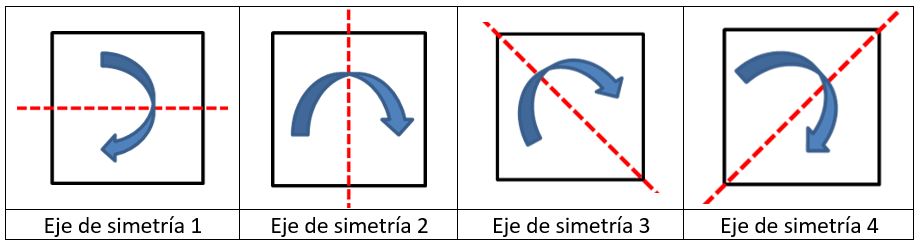
1. Los cuadrados tienen cuatro ejes de simetría

Primero recordemos que la simetría es una correspondencia exacta en tamaño, forma y posición de las partes de un objeto.  Además, tendremos en cuenta que un eje de simetría es una recta que divide a la figura en dos partes idénticas.

Estos ejes de simetría podemos visualizarlos fácilmente con una hoja de papel que tenga los cuatro lados iguales, como la que ves a continuación:

Y puedes hacer estos dobleces para establecer cada eje:

2. Las diagonales de los cuadrados se intersecan en el medio del cuadrado

Una diagonal de un polígono es un segmento de recta cuyos extremos son dos vértices no consecutivos de dicho polígono.

Al trazar las diagonales de un cuadrado estas se cortan en el punto medio del cuadrado, además tienen la misma longitud.

Puedes conseguir el centro de un cuadrado de una hoja de papel realizando los dobleces que hicimos para encontrar el eje de simetría 3 y el eje de simetría 4.

 

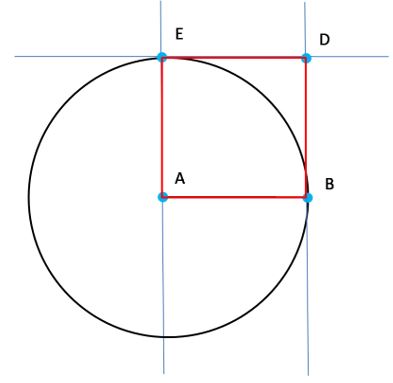
¿Cómo construir un cuadrado?

Para construir un cuadrado podemos seguir estos sencillos pasos:

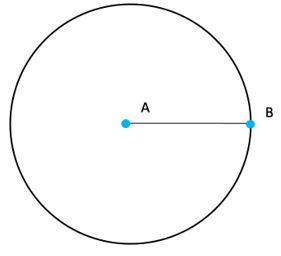
1. Dado el segmento AB vamos a trazar una circunferencia haciendo centro en A y con la abertura del compás de la medida de AB, es decir que el radio es AB.

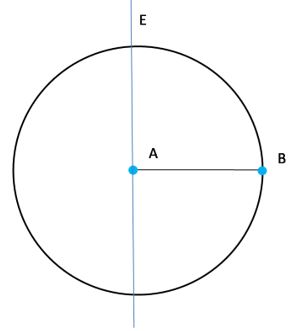
2. Trazamos ahora un segmento perpendicular a AB que contenga al punto A. Y señalamos al punto E, que es la intersección de la perpendicular que acabamos de trazar con la circunferencia.

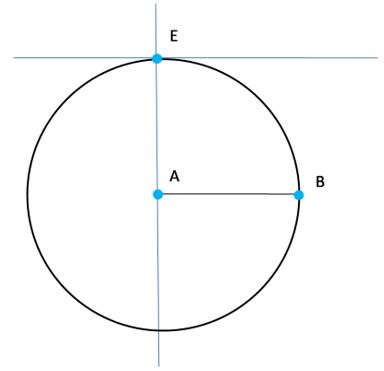
3. Ahora trazaremos la recta paralela al segmento AB que pasa por el punto E.

4. Vamos a trazar ahora la perpendicular al segmento AB que contiene al punto B, y señalamos el punto D, que es la intersección de esta nueva perpendicular con la paralela al segmento AB que trazamos en el paso anterior.

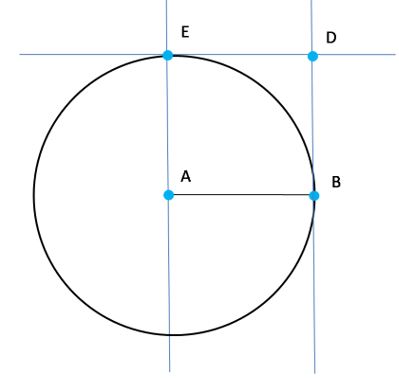
5. Ya podemos trazar el cuadrado ABDE

 

¿Qué son los rectángulos?

Los rectángulos son paralelogramos con cuatro ángulos rectos.

Los rectángulos tienen distintas formas de representarse, veamos algunas en la siguiente trama de puntos.

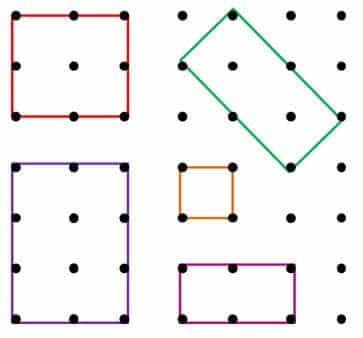
Observa que en todos los casos representados en la trama de puntos son paralelogramos con sus cuatro ángulos rectos, es decir, son rectángulos.

 

Propiedades de los rectángulos

1. Los lados opuestos tiene igual longitud.

Para verificar esta propiedad tomaremos una hoja de papel  con forma rectangular y haremos coincidir sus extremos tanto horizontal como verticalmente.

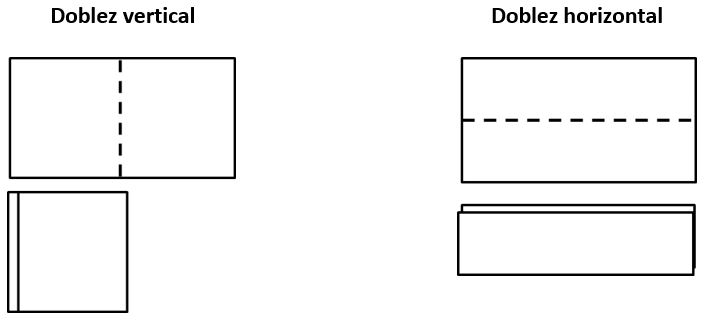
Al doblar la hoja de papel haciendo coincidir sus extremos, tanto horizontal como verticalmente, nos damos cuenta que los lados opuestos son de igual medida. También, se dice que los lados de un rectángulo son iguales dos a dos.

De esta manera verificamos esta primera propiedad de los rectángulos.

2. Las diagonales tienen la misma longitud.

Un rectángulo tiene dos diagonales de igual longitud. Para visualizar esta propiedad utilizaremos una hoja de papel en la que marcaremos sus diagonales.  Luego las mediremos con una regla graduada.

Recuerda que una diagonal es un segmento de recta cuyos extremos son dos vértices no consecutivos del polígono.

Al medir las diagonales con una regla graduada nos damos cuentas que ambas diagonales tienen igual medida.

3. Un rectángulo tiene dos ejes de simetría.

Primero recordemos que un eje de simetría es una recta que divide a la figura en dos partes iguales en forma, tamaño y posición.

Para visualizar esta propiedad trabajaremos nuevamente con una hoja de papel que doblaremos por la mitad tanto horizontal  como verticalmente.  Veamos:

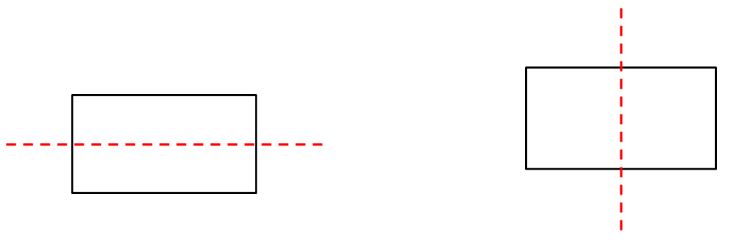
Las líneas que hemos destacado en rojo son los ejes de simetría del rectángulo.

 

Construyendo rectángulos

En este apartado aprenderemos a construir rectángulos con regla y compás.

 

Construcción de un rectángulo dadas las medidas de sus lados

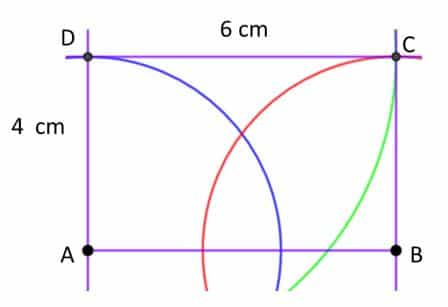
En este caso la base del rectángulo mide 6 cm y su altura 4 cm.

1. Comenzaremos trazando el segmento AB de longitud 6 cm que es la base del rectángulo.

2. En este paso trazamos una perpendicular al segmento AB desde el extremo A.

¿

3. Ahora toma el compás y ábrelo hasta obtener una abertura igual a la altura del rectángulo que en este caso es igual a 4 cm. Luego, haciendo centro en A traza un arco de circunferencia que corte a la recta perpendicular al segmento AB que pasa por el punto A. Este punto es un vértice del rectángulo y lo llamaremos D.

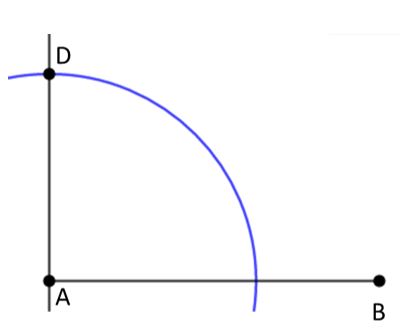
4. Con la misma abertura que utilizamos en el paso 3 y ahora haciendo centro en B trazamos un arco de circunferencia. Veamos:

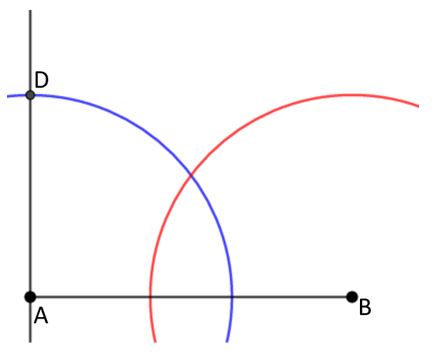
5. Continuamos, ahora abre tu compás con una medida igual a la del segmento AB. Haz centro en D, traza un arco que corte al arco trazado desde B. El punto de corte de los arcos, es el cuarto vértice del rectángulo, lo identificaremos con la letra C.

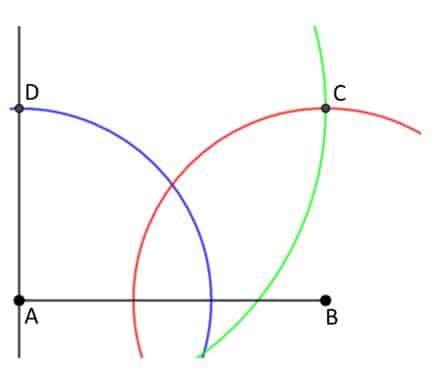
6. Trazamos los segmentos BC y CD. De esta manera obtenemos el rectángulo ABCD.

 

¿Qué son los rombos?

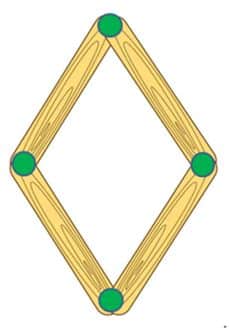
Haciendo rombos con paletas de helados

Vamos a construir un rombo con paletas de helados.

¿Qué necesitamos?

• 4 Paletas de helados de igual tamaño  y 4 Tachuelas.

¿Cómo construimos un rombo con paletas de helados?

• Toma dos paletas de helados. Coloca uno de los extremos de la paleta sobre el extremo de la otra paleta. Hazlo de tal modo que al colocar un extremo sobre el otro podamos encajar una tachuela para que las paletas queden juntas.
• Repite este proceso con las otras dos paletas.
• Luego, une los dos pares de paletas por los extremos que están sueltos, coloca una tachuela en cada uno. Observa la figura para que sepas cómo se debería ver tu rombo.

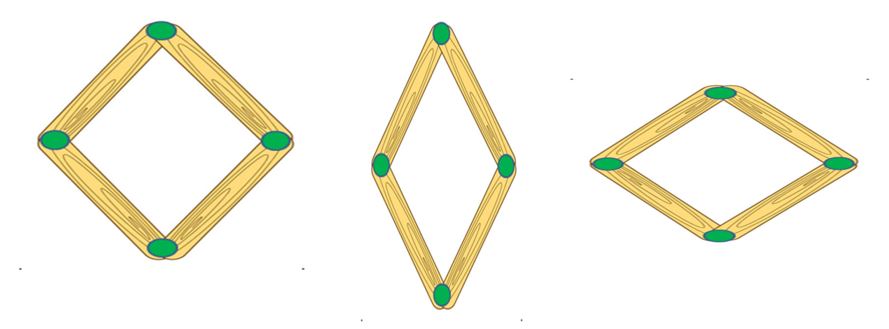
• Ya hemos construido un modelo físico del rombo. Ahora puedes mover las paletas de tal manera que obtengas rombos distintos con cada movimiento. Por ejemplo:

Propiedades de los rombos

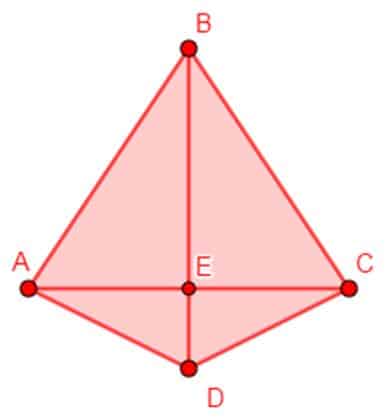
1. Las diagonales de un rombo son perpendiculares.

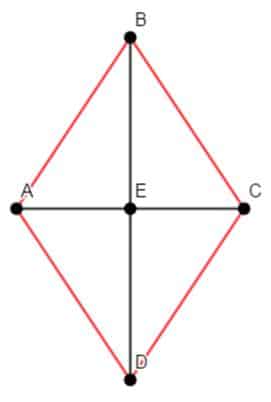
Lo primero que diremos es que un rombo tiene dos diagonales, la de mayor longitud se denomina diagonal mayor y la de menor longitud se llama diagonal menor. En la figura tenemos el rombo ABCD, la diagonal mayor es el segmento BD y la diagonal menor es el segmento AC.

Para verificar que las diagonales AC y BD son perpendiculares en el punto E,  medimos con un transportador el ángulo BEC.

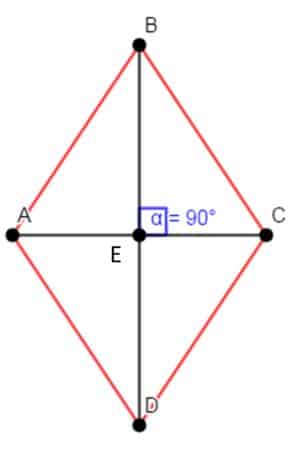
Al medir con el transportador se obtiene que el ángulo BEC mide 90º, lo que verifica que AC y BD son perpendiculares.

 

Construcción de un rombo dadas las medidas de sus diagonales

Veamos cómo podemos construir un rombo en unos pocos y sencillos pasos.

• Construiremos un rombo conocidas las medidas de sus diagonales, en este caso las medidas son: 7 cm y 4 cm.

1. Trazaremos el segmento AB = 7 cm que es la diagonal mayor.

2. Ahora trazaremos la mediatriz del segmento AB. Esta construcción nos permitirá obtener una recta perpendicular al segmento AB en su punto medio.

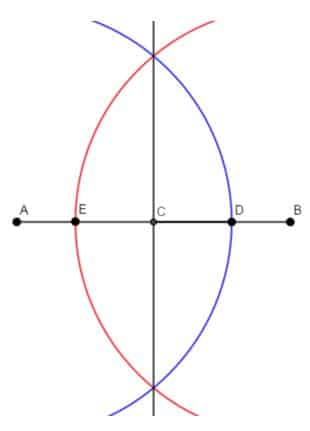
3. Ahora sobre la mediatriz y centrando en C, marcamos con la ayuda de una regla graduada la medida de la diagonal menor, que en este caso es cuatro centímetros. Como debemos hacer centro en C marcamos 2 cm por debajo de C y 2 cm por arriba de C y de esta manera obtenemos la diagonal menor del rombo que es igual a 4 cm. Estos puntos los nombraremos con las letras F y G.

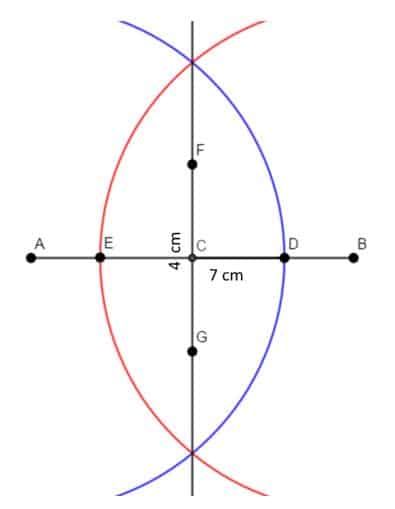
4. Por último, trazamos los segmentos AF, FB, BG, GA, obteniendo el rombo AGBF.

 

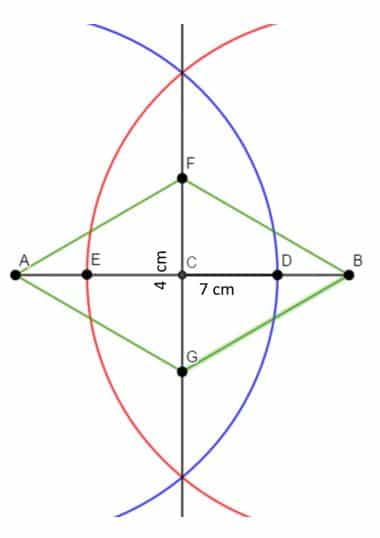
¿Qué son romboides?

Jugando con rompecabezas

• En esta oportunidad el reto es construir un romboide con estos dos triángulos.

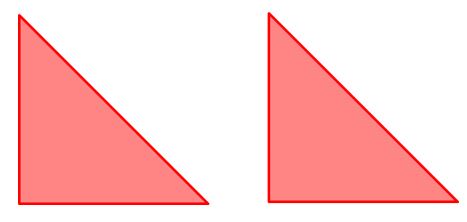
• Piensa rápido: ¿cómo podemos hacerlo?
• Lo primero que  hacemos  es girar el triángulo de la izquierda 180º en sentido contrario a las agujas del reloj.

• Luego trasladamos el triángulo de la derecha hacia la izquierda hasta que coincidan los catetos de ambos triángulos.

• De esta manera obtenemos un romboide a partir de dos triángulos.

Propiedades de los romboides

1. Los lados opuestos y paralelos son de igual medida.
2. Posee dos ángulos agudos y dos obtusos.
3. El punto en el que se cortan las dos diagonales es el centro del romboide.

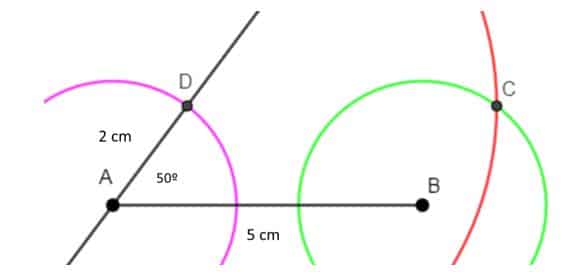
Construcción de un romboide dadas las medidas de sus lados y los ángulos agudos

En este caso la medida de los lados son 5 cm y 2 cm. Mientras que los ángulos agudos miden 50º cada uno.

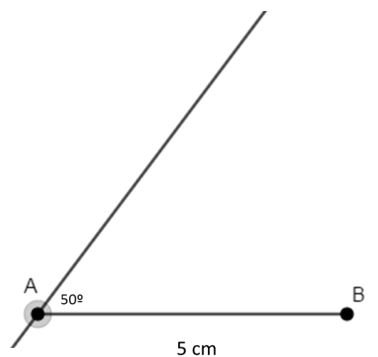
1. Lo primero que haremos será trazar el segmento AB cuya longitud es igual a 5 cm. Este segmento será la base del romboide.

2. Ahora con el transportador centrado en A, construimos el ángulo de 50º.

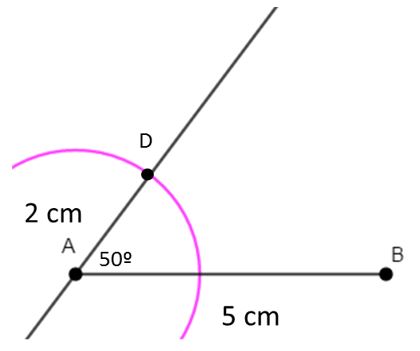
3. Ahora abrimos el compás con una abertura igual a 2 cm, que es la medida del lado contiguo a AB. Seguidamente, haciendo centro en A con el compás, trazamos un arco de circunferencia que corte el lado del ángulo. El punto donde se cruzan es un vértice del romboide, lo denotaremos con la letra D.

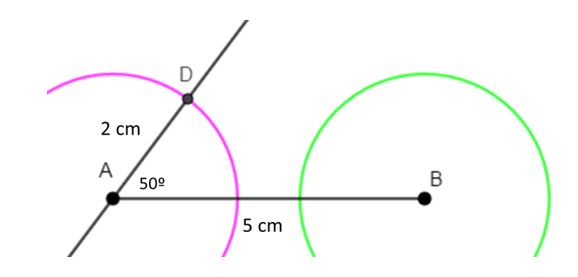
4. Con la misma abertura del compás que utilizamos en el paso anterior, hacemos centro en B y trazamos un arco de circunferencia.

5. Ahora abrimos el compás con una medida igual a la longitud del segmento AB. Con esta abertura y haciendo centro en D, trazamos un arco de circunferencia que corte al que acabamos de trazar en el paso 4. La intersección de los dos arcos es el cuarto vértice del romboide, lo identificamos con la letra C.

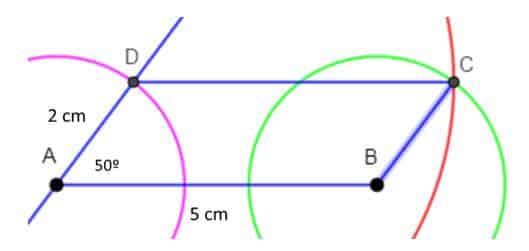
6. Trazamos los segmentos BC y CD. De esta manera queda construido el romboide ABCD.

 

¿Qué son los trapecios?

¿Cuáles son los elementos del trapecio?

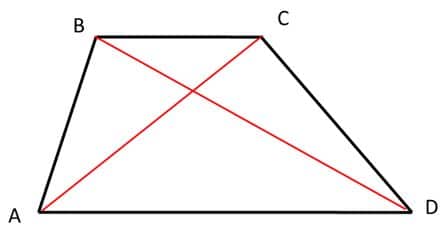
Observa el trapecio ABCD que presentamos a continuación. Lo usaremos para ir señalando cada uno de los elementos de los trapecios: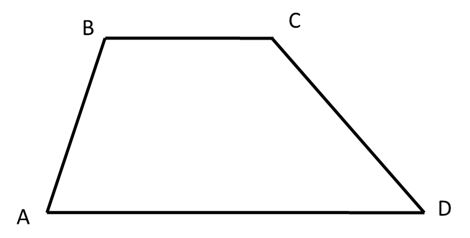

1. Lados: Los trapecios tienen cuatro lados, por ser cuadriláteros. En este caso son los segmentos AB, BC, CD y AD.
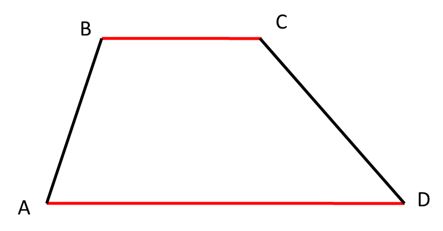
2. Bases: Las dos bases del trapecio son sus lados paralelos. En este caso, son AD y BC.

3. Diagonales: Un trapecio tiene dos diagonales. Recordemos que las diagonales son segmentos de recta cuyos extremos son dos vértices no consecutivos del polígono.

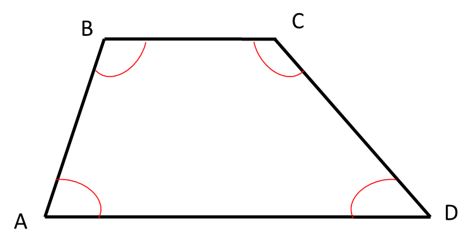
4. Ángulos: Los trapecios tienen cuatro ángulos que suman 360°, como en todos los cuadriláteros:

Las medidas de los ángulos de los trapecios nos permiten clasificarlos, y eso lo veremos a continuación.

¿Cómo se clasifican los trapecios?

Como dijimos anteriormente, los trapecios se clasifican de acuerdo a las medidas de sus ángulos en:

• Trapecio rectángulo
• Trapecio isósceles
• Trapecio escaleno

Veamos qué característica tiene cada uno de ellos.

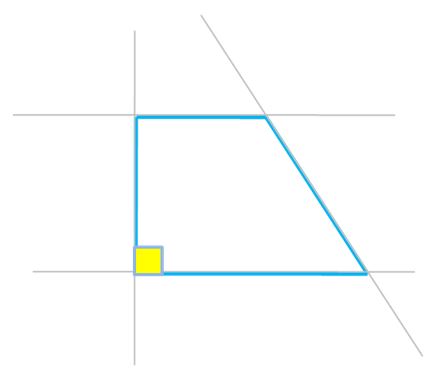
Trapecio rectángulo

El trapecio rectángulo posee dos ángulos rectos, pues uno de los lados que no son paralelos es perpendicular a las bases.

Trapecio Isósceles

En los trapecios isósceles los lados no paralelos son iguales.

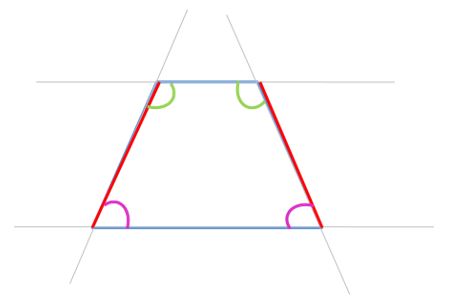
Además, poseen dos ángulos agudos y dos ángulos obtusos. Y los ángulos contiguos son congruentes.

Trapecio escaleno

Este tipo de trapecio no tiene ángulos rectos, ni posee lados paralelos iguales. Sus ángulos son todos de diferente medida.

 

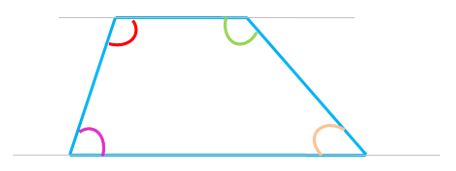
¿Qué son los trapezoides?

Los trapezoides son cuadriláteros sin lados paralelos.

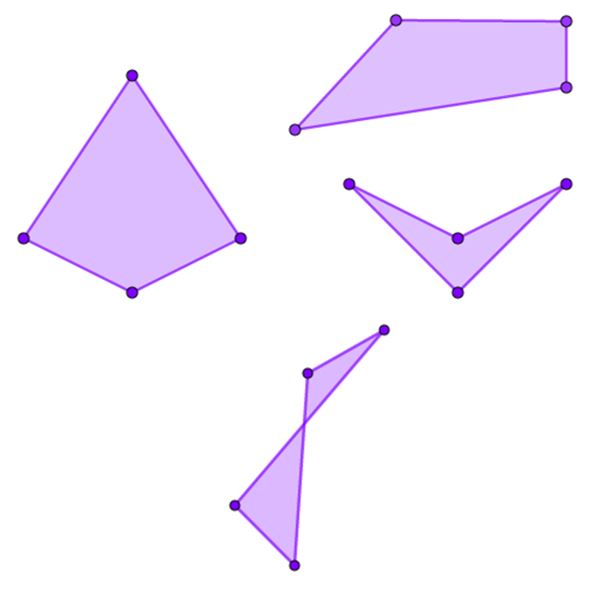
Los tipos de trapezoides son:

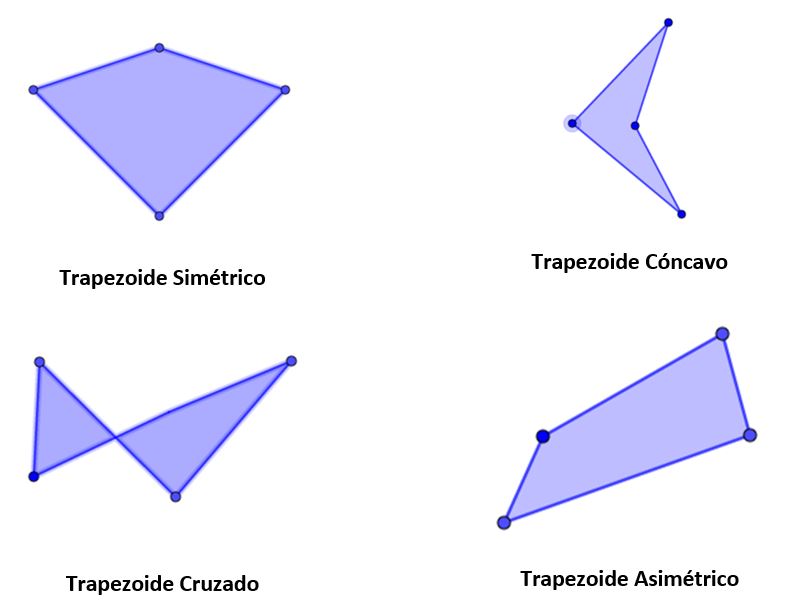
¿Cómo son las diagonales de los trapezoides?

• Trapezoide Simétrico: Las diagonales del trapezoide simétrico son perpendiculares.

• Trapezoide Cóncavo: Al prolongar una de las diagonales del trapezoide cóncavo, éstas se intersectan en un punto exterior al trapezoide.

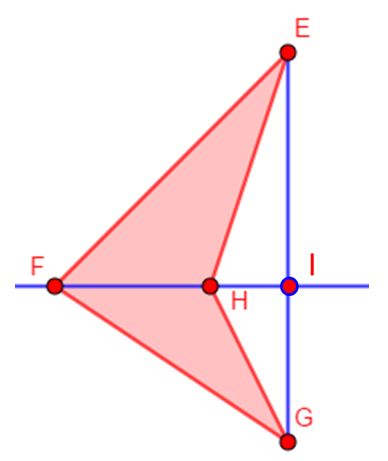
• Trapezoide Cruzado: Las diagonales al ser prolongadas se cortan en un punto exterior al trapezoide.

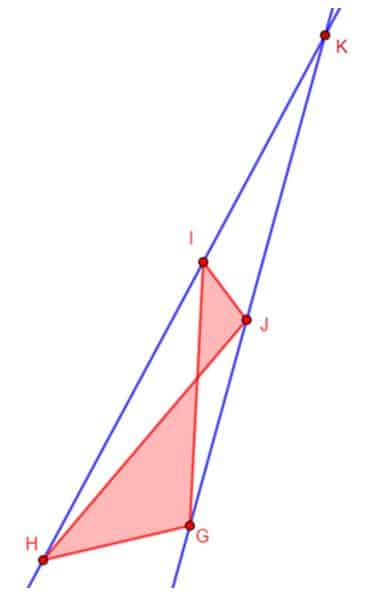
• Trapezoide Asimétrico: Las diagonales se cortan en un punto interior del trapezoide.

 

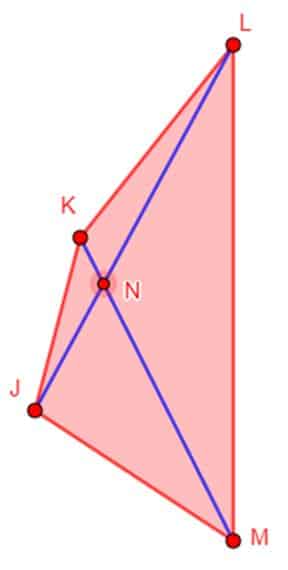
Antes de dar por finalizado este texto sobre los cuadriláteros con el que has podido conocerlos en profundidad, hemos preparado una recopilación de los datos más importantes para que puedas descargarla y ayudarte a recordar y a estudiar si ese fuese el caso.

Selecciona un juego 👇 👇 👇

Registrado en SafeCreative.