Propiedades de la suma
Las matemáticas están llenas de reglas que nos ayudan a entender mejor cómo funcionan los números. Una de esas reglas son las propiedades de la suma, que explican cómo se comportan los números cuando los sumamos de distintas formas.
¿Sabías que puedes cambiar el orden de los números o agruparlos de forma diferente y el resultado sigue siendo el mismo? ¿Y que hay un número que no cambia nada cuando lo sumas? Todo eso lo explican estas propiedades.
En esta página aprenderás de forma clara y con ejemplos qué es la propiedad conmutativa de la suma, la propiedad asociativa y cuál es el elemento neutro. Además, verás por qué son útiles en la vida diaria y podrás practicar con ejercicios sencillos.
¿Qué son las propiedades de la suma?
Las propiedades de la suma son reglas matemáticas que nos ayudan a entender cómo funciona la suma, sin importar los números que usemos. Gracias a estas propiedades, podemos sumar más rápido, comprobar resultados y resolver operaciones de forma más fácil.
Hay tres propiedades principales que debes conocer:
- La propiedad conmutativa, que nos permite cambiar el orden de los números.
- La propiedad asociativa, que nos permite agrupar los números de distintas formas.
- El elemento neutro, que es un número especial que no cambia nada al sumarlo.
Estas propiedades no solo sirven para aprobar exámenes, ¡también son muy útiles en la vida diaria! Y lo mejor es que son fáciles de aprender si las vemos con ejemplos claros.
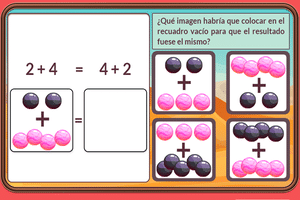
Propiedad conmutativa de la suma
Definición y explicación
En palabras simples:
Si cambias el orden de los números, la suma no cambia.
Ejemplos prácticos
\[
3 + 5 = 8
\]
\[
5 + 3 = 8
\]
➡️ En ambos casos el resultado es 8, aunque los números estén en distinto orden.
\[
2{,}5 + 4 = 6{,}5
\]
\[
4 + 2{,}5 = 6{,}5
\]
Truco para recordarlo: “Cambiar el orden no cambia el total.”
Propiedad asociativa de la suma
Definición y explicación
En palabras sencillas:
Puedes poner paréntesis donde quieras y la suma seguirá siendo la misma.
Ejemplos prácticos
\[
(2 + 3) + 4 = 5 + 4 = 9
\]
\[
2 + (3 + 4) = 2 + 7 = 9
\]
➡️ El resultado es el mismo: 9, aunque agrupes de forma distinta.
\[
(1 + 2) + 6 = 3 + 6 = 9
\]
\[
1 + (2 + 6) = 1 + 8 = 9
\]
Truco para recordarlo: “Agrupar de forma distinta no cambia la cuenta.”
Elemento neutro de la suma
¿Qué es el elemento neutro?
Ejemplos prácticos
\[
5 + 0 = 5
\]
\[
0 + 12 = 12
\]
\[
0 + 0 = 0
\]
\[
7{,}3 + 0 = 7{,}3
\]
Truco para recordarlo: “Sumar cero no cambia nada.”
Importancia de las propiedades de la suma en la vida cotidiana
Puede que te preguntes: “¿Para qué me sirve aprender esto fuera del cole?” 🤔
La verdad es que las propiedades de la suma están por todas partes, aunque no siempre nos demos cuenta.
Al hacer compras
Si compras una barra de pan y un zumo, da igual el orden en que sumes los precios:
\[
0{,}80 + 1{,}20 = 2{,}00
\]
\[
1{,}20 + 0{,}80 = 2{,}00
\]
¡Propiedad conmutativa en acción!
Al hacer cálculos mentales
Si tienes que sumar varios números, puedes agrupar primero los que te resultan más fáciles:
\[
(10 + 20) + 5 = 30 + 5 = 35
\]
\[
10 + (20 + 5) = 10 + 25 = 35
\]
¡Eso es usar la propiedad asociativa!
Al evitar operaciones innecesarias
Si ves un cero en la suma, sabes que no cambia nada:
\[
25 + 0 = 25
\]
¡Elemento neutro al rescate!
Estas propiedades te ayudan a pensar más rápido, organizar mejor las operaciones y cometer menos errores.