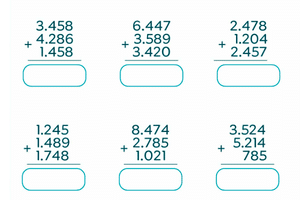
Sumas con llevadas

Sumar es una de las habilidades básicas de la aritmética, y es de las operaciones que más temprano se aprenden a hacer. Existen varios tipos de sumas, entre ellas están las sumas con llevadas, o sumas llevando.

Es muy importante que manejes este tipo de sumas, y que las aprendas a hacer muy bien, para que puedas incluso resolverlas mentalmente. En este artículo aprenderás cómo hacer sumas llevando fácilmente, tanto con dos cifras como con tres cifras, y a resolver problemas de sumas llevando paso a paso.

 

¿Cómo hacer sumas con llevadas?

El principio que está detrás de “llevar” cuando sumamos se basa en el funcionamiento de nuestro Sistema de Numeración Decimal.

Por ello, para aprender cómo hacer sumas llevando debes tener presente que:

10 unidades = 1 decena

10 decenas = 1 centena

 

Además, debes saber que el sistema de Sistema de Numeración Decimal es muy eficiente:

Veamos esto en el cartel de valor con ejemplos:

• Ejemplo 1:

9 + 7

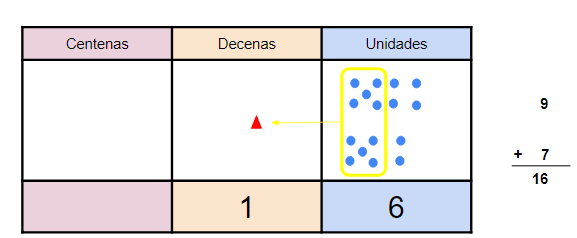
• • Como puedes ver, en el orden las unidades hemos agrupado 10 elementos y los convertimos en 1 decena, pues sólo se admiten 9 elementos en cada orden.
  • Entonces tenemos 1 decena y 6 “unidades sueltas”, o unidades sin agrupar.
  • Ten en cuenta siempre que las llamamos “unidades sueltas”, o “decenas sueltas” porque no llegan a ser 10 para agruparlas y formar 1 elemento del orden siguiente.

 

 

• Ejemplo 2:

83 + 71

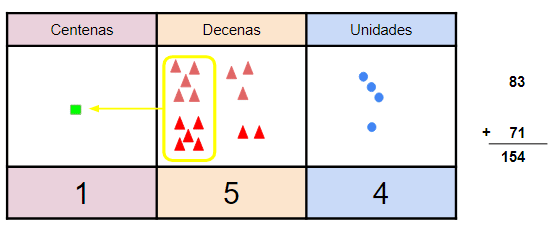
• • Aquí hemos agrupado 10 decenas y las pasamos al orden siguiente como 1 centena. Recuerda que sólo “caben” 9 elementos en cada orden.
  • Nos quedaron 1 centena, 5 “decenas sueltas” y 4 “unidades sueltas”.

 

Emplea los carteles de valor de las siguientes fichas para hacer las sumas indicadas.

 

Sumas de dos cifras llevando

En este apartado explicaremos las sumas de dos cifras llevando paso a paso. Para ello nos apoyaremos en el ábaco, que es un excelente recurso para cuando te inicias en el cálculo.

Mira este  ejemplo de cómo se representan números en el ábaco para que comprendas todo lo que vamos a explicar:

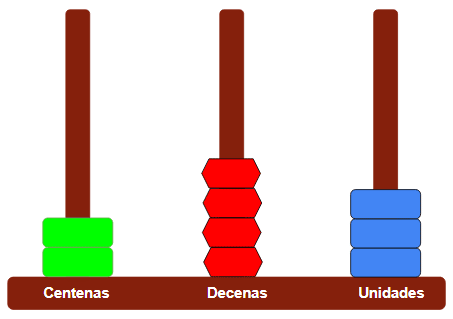
El número representado es 243.

• Las fichas azules representan las unidades.
• Las fichas rojas representan las decenas.
• Las fichas verdes representan las centenas.
• Debemos recordar que en cada orden sólo caben 9 fichas.

• Resuelve la siguiente operación: 45 + 27
  • Veamos cómo la resolvemos con el ábaco.
  • Tenemos 45 unidades representadas en el ábaco:

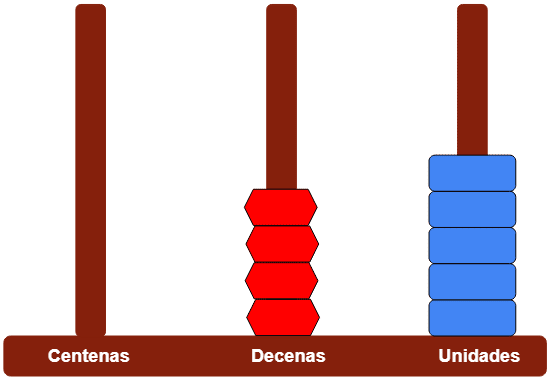
• • 4 fichas en el lugar de las decenas y 5 fichas en el lugar de las unidades.
  • Ahora vamos a agregar 27 unidades, que serían 2 fichas en el lugar de las decenas y 7 fichas en el lugar de las unidades.
  • Empecemos agregando las 7 unidades a las 5 que ya están allí. Tendríamos 12 fichas en las unidades.

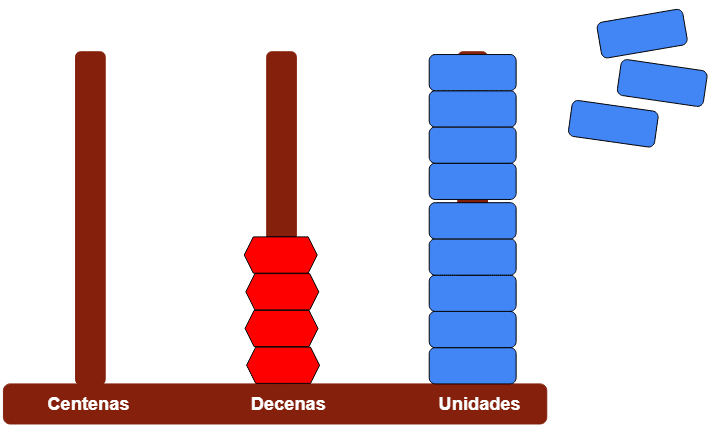
• • Como puedes ver, no caben todas. Tendremos que agrupar algunas unidades en decenas para que puedan caber. Recuerda que:

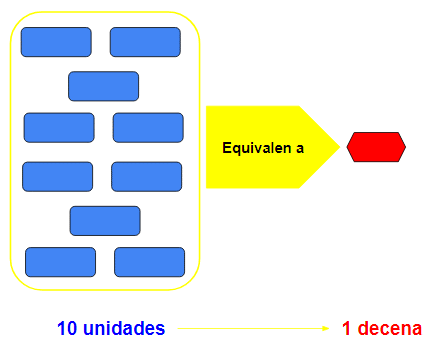
• • Entonces, agrupamos 10 fichas azules y las cambiamos por una roja. Nos quedan entonces 2 azules “sueltas” en las unidades, de las 12 que teníamos.

• • Ahora agregamos las 2 decenas, es decir, las 2 fichas rojas que completan el 27 que estábamos sumando a 45. Nos queda así:

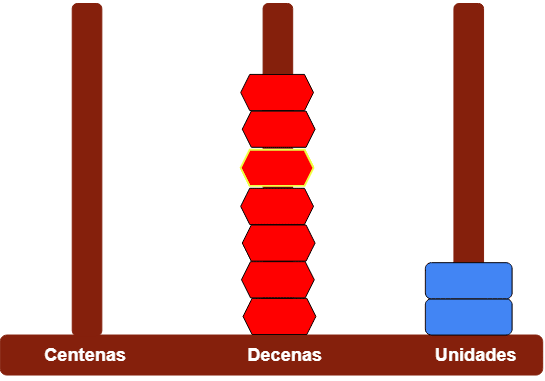
• • Quedan representadas 7 decenas y 2 unidades sueltas. Esto es equivalente a 72 unidades
  • Por último, tenemos que 45 + 27 = 72
  • Cuando ya hemos entendido el principio explicado anteriormente, esta suma con llevadas se hace así:

 

 

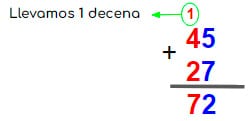
• ¿Cuánto es 36 + 89?
  • Para resolver esta adición usaremos el ábaco.
  • Representamos en el ábaco el número 36. Serían 3 fichas rojas en las decenas y 6 fichas azules en las unidades.

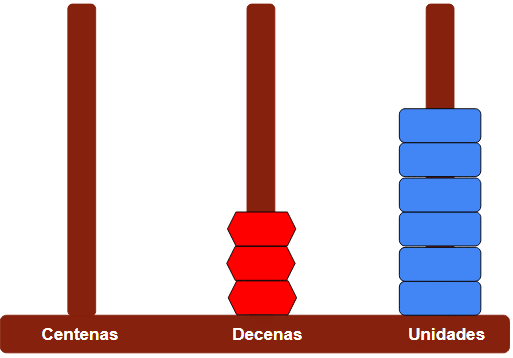
• • Ahora sumamos 89 a las 36 que ya tenemos.
  • Es decir, 8 fichas rojas en las decenas y 9 fichas azules en las unidades.
  • Empezamos con las unidades:

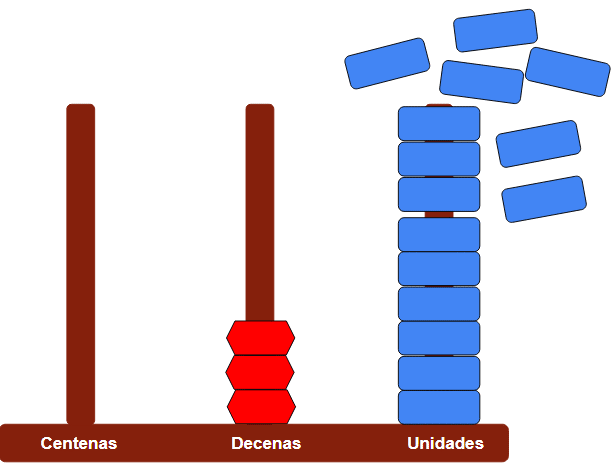
• • Tenemos ahora 15 fichas azules.
  • Como no caben todas las fichas azules en las unidades debemos agruparlas en decenas para llevarlas a ese orden.
  • Recuerda que 10 fichas azules equivalen a 1 ficha roja.
  • Al agruparlas y llevar a las decenas nos quedan así:

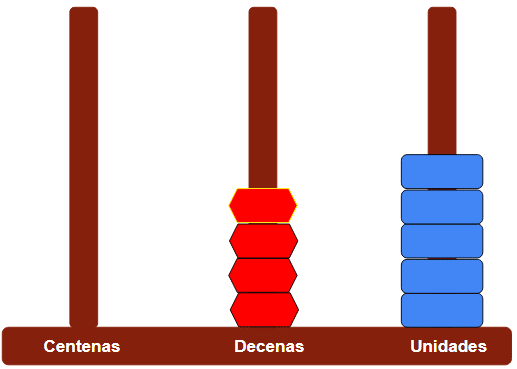
• • Ahora sumamos las decenas de 89. Es decir, sumamos 8 decenas o fichas rojas.

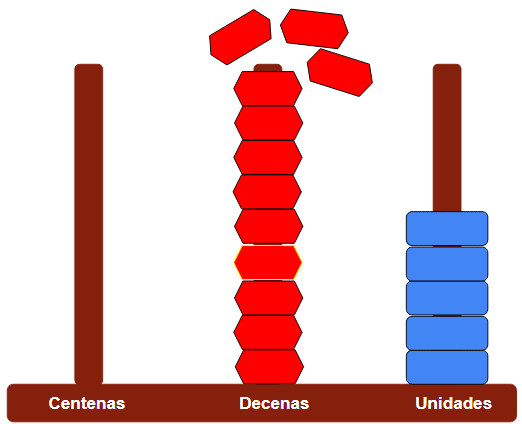
• • Ahora tenemos 12 decenas, contando con la que llevamos.
  • Como no caben todas debemos agrupar 10 para formar 1 centena. Recuerda que:

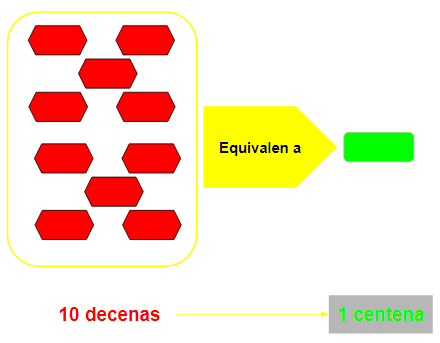
• • Nos queda así:

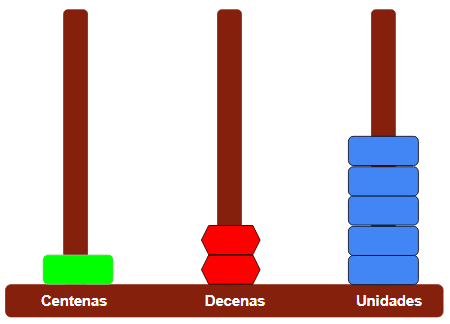
• • Podemos decir que 36 + 89 = 125
  • Una vez hayamos comprendido esto, podemos hacerlo de forma vertical así:

 

Para practicar la suma de dos cifras llevando, te ofrecemos la siguiente ficha:

 

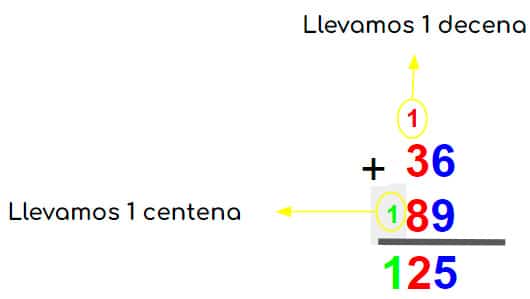
Sumas de tres cifras llevando

En esta parte del artículo te explicamos cómo hacer una suma de tres llevando paso a paso. Para ello, nos apoyaremos en el cartel de valor. Veamos:

• 265 + 376
  • Lo representamos así en el cartel de valor:

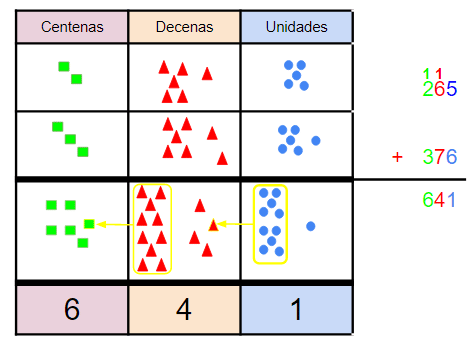
• • Fíjate cómo hemos agrupado 10 unidades llevando 1 decena.
  • Luego, agrupamos 10 decenas llevando 1 centena.

 

• 785 + 858
  • Al representarlo en el cartel de valor tenemos:

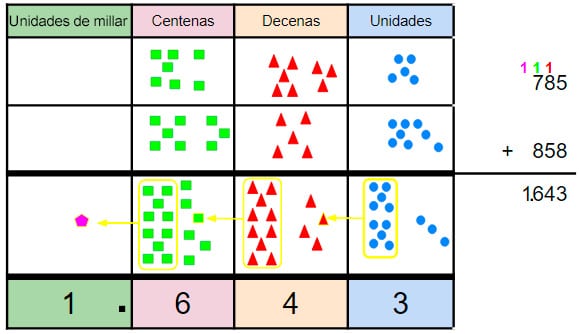
• • Como puedes observar hemos agrupado así:
    • 10 unidades para llevar 1 decena.
    • 10 decenas para llevar 1 centena.
    • 10 centenas para llevar 1 unidad de mil.

 

Ahora es el turno de practicar la suma de tres cifras llevando con las propuestas que aparecen a continuación:

 

Problemas de sumas de dos cifras llevando

Ahora vamos a resolver problemas de sumas de dos cifras llevando, lo haremos teniendo en cuenta que los problemas aditivos son bastante comunes en la vida cotidiana. Presta mucha atención para que seas todo un experto resolviendo este tipo de situaciones problemáticas.

Lee con atención y resuelve los siguientes problemas:

 

1. Andrea ahorró 78 euros en enero y 23 euros en febrero. ¿Cuánto dinero tiene ahorrado Andrea en estos dos meses?

• • El problema nos dice que Andrea ahorró 78 € en enero y 23 € en febrero. Queremos saber cuánto dinero lleva ahorrado hasta el momento. Ordenemos esta información en una tabla. 

• • Para determinar el dinero ahorrado por Andrea durante estos dos meses, vamos a sumar:

78 + 23

• • Veamos:

 

• • En el gráfico se observa que hemos sumado orden a orden 78 + 23. Es decir, hemos adicionado 8 unidades + 3 unidades y 7 decenas + 2 decenas, obteniendo como resultado 101 unidades.
  • Recuerda que el mayor número de elementos que admite cada orden es 9. Al tener 10 elementos es necesario agruparlos y llevarlos al orden inmediatamente superior, como una nueva unidad en ese orden.
  • Es decir 10 unidades equivalen a 1 decena y 10 decenas equivalen a 1 centena.
  • Respondiendo a la pregunta del problema, tenemos que Andrea tiene ahorrado 101 €.

 

2. ¿Qué resultado se obtiene al sumar 46 con el mayor número de dos cifras?

• • Lo primero que haremos será establecer que 99 es el mayor número de dos cifras.
  • Ahora realicemos la adición:

99 + 46

• • En el gráfico observamos la suma de 99 + 46. Hemos sumado orden a orden, haciendo agrupaciones de 10 elementos cada vez que lo hemos necesitado.  Recuerda que el mayor número de elementos que admite cada orden es 9.
  • De esta manera, el resultado de sumar 99 (el mayor número de dos cifras) más 46 es 145.

 

 

Problemas de sumas de tres cifras llevando

En esta sección estudiaremos cómo resolver problemas de sumas de tres cifras llevando.

1. Carlos almacena agua en dos recipientes distintos. El primero tiene una capacidad de 728 litros y el segundo cuenta con una capacidad de 386 litros. ¿Cuál es la mayor cantidad de agua que puede almacenar Carlos en estos dos recipientes? 

• • Para saber cuál es la mayor capacidad de agua que Carlos puede almacenar en los dos recipientes, sumaremos 728 + 386. Realizaremos esta operación en el cartel de valor. Veamos:

• • En el gráfico representamos la adición 728 + 386. En el orden de las unidades hemos hecho una agrupación de 10 elementos que equivalen a 1 decena, quedando 4 elementos en el orden de las unidades.
  • Luego, realizamos la adición que corresponde en el orden de las decenas. Fue necesario realizar una agrupación de 10 elementos en este orden que equivalen a 1 centena. Y nos ha quedado 1 elemento en el orden de las decenas.
  • A continuación, hicimos la adición  en el orden de las centenas. Como era necesario, realizamos una agrupación de 10 centenas que equivalen a 1 unidad de mil. Quedando en las centenas 1 elemento.
  • En las unidades de mil también quedó 1 elemento.
  • Concluimos, que 728 + 386 = 1.114
  • Respondiendo a la pregunta del problema, la mayor cantidad de agua que puede almacenar Carlos en estos dos recipientes es de 1.114 litros.

 

2. Hay que distribuir las cifras: 9, 7, 6, 4 y 2 en los recuadros del dibujo, de tal manera que al sumar el número de 3 cifras con el número de 2 cifras se obtenga la mayor suma posible:

• • La mayor suma posible la podemos obtener distribuyendo las cifras mayores (9, 7, 6) en las posiciones de la centena y las decenas, y las cifras menores (4, 2), en la posición de las unidades. Veamos:
  • Colocando las cifras mayores en los órdenes de mayor valor posicional, obtenemos que la mayor suma posible es 1.036, esta suma se obtiene de sumar 974 + 62.

 

• ¿Existen otras combinaciones con estos números, que nos permitan obtener la mayor suma posible?

• • La respuesta a esta pregunta es Sí. De hecho hay 3 formas más de combinar los números  9, 7, 6, 4, 2 y obtener la mayor suma posible que es 1.036. Veamos:

• • Lo que hicimos fue intercambiar de posición las cifras que ocupan los órdenes de las decenas y las unidades.
  • De esta manera obtenemos la mayor suma posible que es 1.306 con 4 combinaciones distintas.

 

Antes de dar por concluido el texto, dejamos unas actividades de sumas con llevadas para que practiques. ¡No pierdas la oportunidad!

Selecciona un juego 👇 👇 👇

 

Registrado en SafeCreative.