Juegos de figuras geométricas

Orientación espacial:
situación en el espacio

Líneas rectas, curvas,
poligonales cerradas y abiertas

Los polígonos: definición y figuras básicas

Círculo y circunferencia

Los polígonos y sus elementos

Clasificación de los polígonos
según sus lados

Prismas y pirámides

Cuerpos redondos
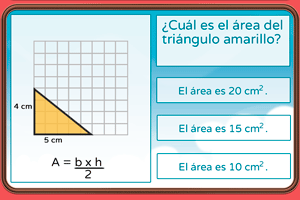
Perímetro y área de triángulos y cuadriláteros

Elementos y clasificación de los ángulos

Figuras simétricas y ejes de simetría
Elementos básicos de los prismas y las pirámides

Tipos y construcción de ángulos

Comparación entre ángulos por su amplitud
Áreas de triángulos y cuadriláteros
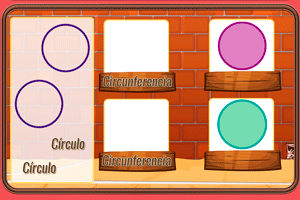
Elementos del círculo y la circunferencia

Posiciones relativas de la recta y la semirrecta
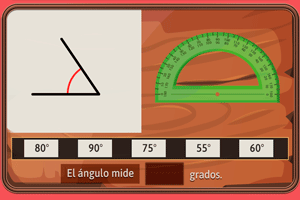
Medida y bisectriz de un ángulo
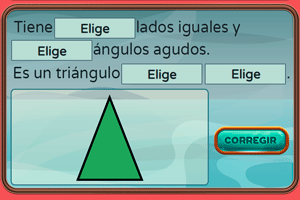
Clasificación de triángulos y cuadriláteros
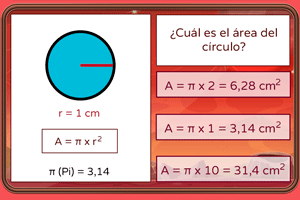
La circunferencia y el círculo: elementos, longitud y área
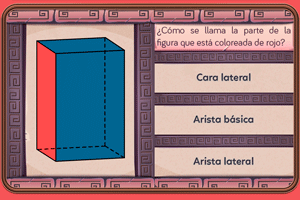
Poliedros y cuerpos redondos

Simetrías, traslaciones y giros
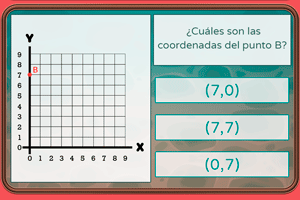
Coordenadas de un punto y ejes de coordenadas
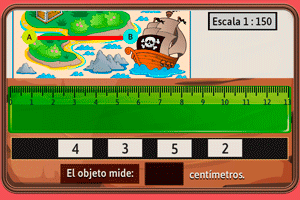
Mapas y escalas numéricas
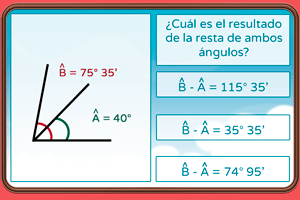
Operaciones con ángulos
y sus unidades de medida

Particularidades de los
triángulos y los cuadriláteros

Perímetro y área de los polígonos

Elementos de la
circunferencia y el círculo

La longitud de la circunferencia
y el área del círculo

Las figuras circulares:
sector, segmento y corona

Cuerpos geométricos y su desarrollo

Área de prismas, pirámides y cilindros
Juegos de Geometría
¿Paralelas, simetría, cuadriláteros, perímetro…? ¿es geometría o deporte? Las tres cosas. Sin embargo, desde Mundo Primaria, nos ocupamos de estos conceptos desde la primera, desde la Geometría. Tratamos de que se entiendan mejor y se manejen con la misma soltura que los profesionales que utilizan sus otros significados.
¿Cómo van a colaborar los tipos de triángulos y las rectas perpendiculares en alcanzar objetivos tan ambiciosos?
La respuesta es obvia, la tenemos delante de los ojos continuamente, tanto que nos pasa desapercibida. La Geometría parte de lo que nos rodea y de nosotros/as mismos/as. ¿Acaso la pantalla que tienes delante no es un rectángulo? ¿La taza de café o cacao a la que, tal vez, tienes tanto cariño no es un cilindro con asa? ¿No son nuestros cuerpos tipos de líneas? Unas más rectas, otras más curvas; pero líneas rectas y líneas curvas, al fin y al cabo.
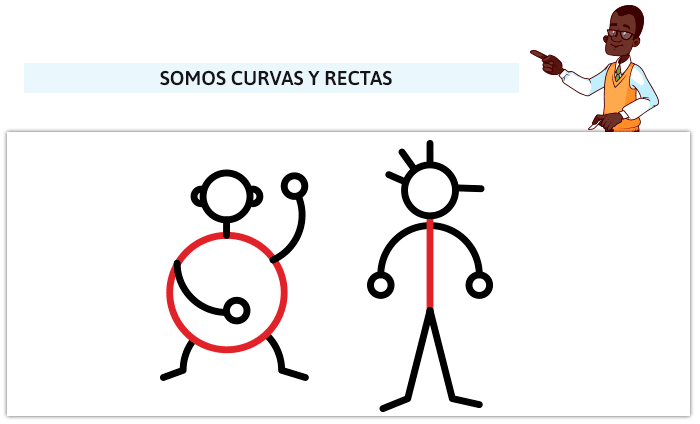
Bromas aparte, la Geometría tiene su origen en la naturaleza. De hecho, la palabra procede del griego “medida de la tierra”. Así pues, vamos a dedicarle unos párrafos y, si nos sigues, recorreremos juntos una breve descripción (aunque pueda parecer larga) de muchas de las cosas que tenemos la suerte de aprender en Primaria e, incluso, en Infantil. ¿Por qué privar a los/as “peques” del sistema educativo de jugar con los tipos de triángulos y cuadriláteros, divertirse con juegos de cubos, buscar esferas en el patio y círculos en los platos del comedor?
Ángulos sin transportador y figuras geométricas sin regla
Como poder dibujarse, se pueden. Ahora bien, si esperamos que dichas líneas abiertas y líneas cerradas sean de verdad poligonales y no más o menos líneas curvas, no nos queda más remedio que practicar la motricidad ojo-mano con los instrumentos de dibujo.
A todos y todas nos encanta cuando nos compran o compramos un juego de reglas con su escuadra, su cartabón, su transportador, etc. No obstante, a la hora de usarlos nos agobiamos y parece que, en lugar de 10 dedos, tenemos 20; y que el espacio de una hoja de papel es demasiado poco. ¿Por qué no se puede presentar al/a profesor/a la mesa donde ha terminado de trazarse la bisectriz de un ángulo? ¡Con las florituras que hay que hacer con el compás y las reglas, de repente no sirve de nada porque el tablero de la mesa no entra en la mochila! En fin… En la práctica está la clave. Así pues, para hacernos una idea real de cómo trazar figuras geométricas y ángulos sin acabar con un esguince de muñeca ni adaptando muebles al espacio de las carteras, empezaremos por presentar los utensilios de dibujo que se manejan en el colegio.
Comencemos con el punto y la línea
Al inicio de la Primaria nos hablan de la línea; pero el origen real es el punto, ya que una fila de puntos (como si fuesen hormiguitas en busca de alimento) forma dicha línea. El uso de esta palabra, en lugar de recta, se debe a que no todas las sucesiones de puntos van siempre en organización militar, a veces, alguno se despista, se va hacia un lado u otro y trazan líneas curvas.
La recta y sus posiciones relativas
La recta es un tipo de línea en la que todos sus puntos van realmente en fila y es importante mencionar que la línea recta es ilimitada: nunca será posible contar todos sus puntos porque siempre posee más y más. Así que se suele utilizar un segmento o varios de ella. Por si no ha quedado muy claro, se podría decir que un segmento tiene principio y final; es como si la recta fuese una cinta y con unas tijeras le cortásemos un trocito (hacemos dos cortes). Algo muy distinto a la semirrecta, la cual supone hacer un solo corte. De esta manera, divides la recta en dos y ambas partes tienen principio, pero no final.
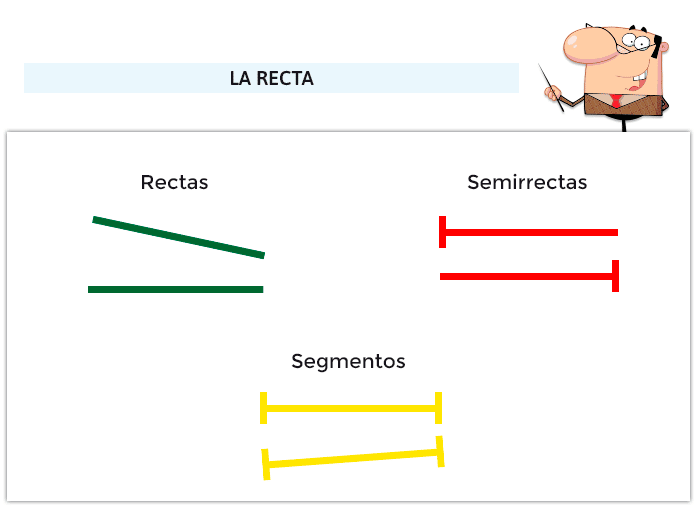
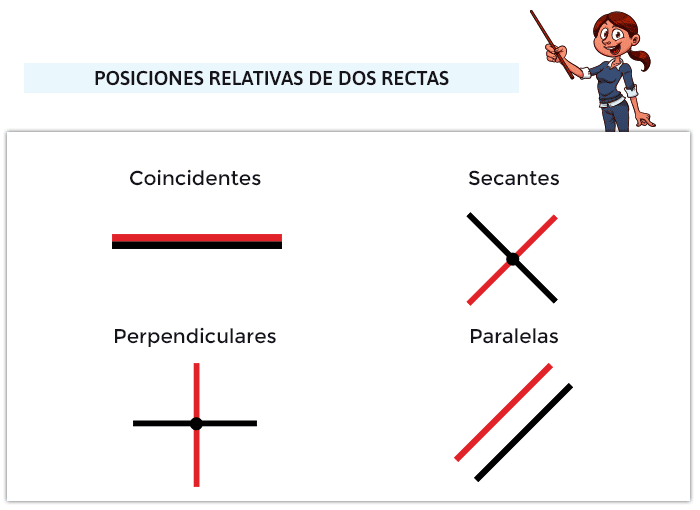
Igualmente, debemos señalar que, en ocasiones, las rectas se encuentran con otras rectas en el mismo plano y dan lugar a ángulos y puntos en común: estas posiciones se llaman coincidentes (todos los puntos en común); secantes (un solo punto en común); o perpendiculares, que son un caso especial de las secantes porque forman cuatro ángulos rectos. Además, pueden no encontrarse nunca y se les llaman rectas paralelas.
Líneas abiertas y líneas cerradas
Retomando el tema de la línea, independientemente de si es recta o no, hay una distinción importante que hacer: en una línea, cuando el primer punto se une con el último, esta se convierte en una línea cerrada; pero si esto no sucede entrará en el grupo de las líneas abiertas.
Por último, no se nos pueden olvidar las líneas poligonales cerradas y abiertas: ambas surgen de la unión de segmentos. La diferencia está en si los segmentos de sus extremos coinciden en un punto o no. Seguro que con los siguientes dibujos se entiende mucho mejor y es más sencillo de lo que da a entender tanta definición.
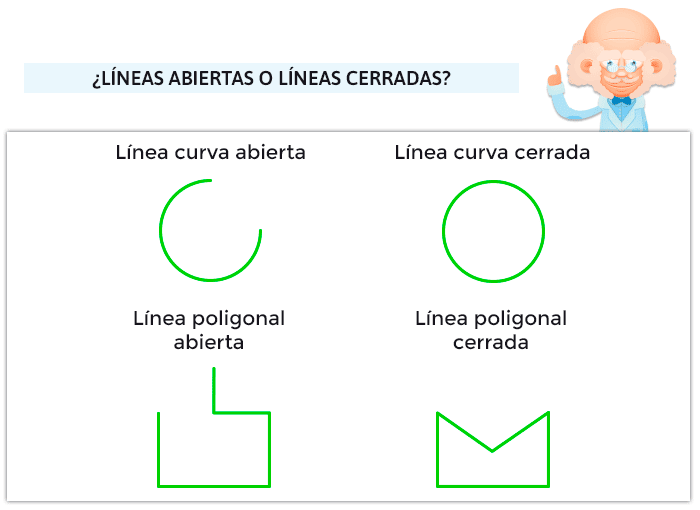
¿A qué era más fácil de lo que parecía? Pues, en cuanto leas el siguiente apartado sobre los ángulos que pueden formar los tipos de líneas rectas, retomar después la composición de figuras geométricas te resultará de todo menos complejo. Ya lo verás.
Todo lo que debemos saber sobre los ángulos para pasar airosos/as la primaria y los niveles de los juegos en mundo primaria
Para que esto sea una gran verdad, hay que decir que un ángulo está formado por dos rectas secantes: ambas coinciden en un punto al que llamamos vértice, y el resto de puntos pasan a formar lo que nombramos como lados. Los ángulos tienen una amplitud que se mide en grados gracias al famoso transportador.
Tipos de ángulos según su medida, su posición y su suma
Los ángulos, al igual que los números o los polígonos, también pueden clasificarse. Cuando terminamos Primaria somos capaces de nombrar un ángulo según la abertura que tiene, por su posición con respecto a otro o por cuánto suman dicho ángulo y un amigo con el que comparte vértice.
Tipos de ángulos según su medida
En el primer caso, nos encontramos con los ángulos agudos (menores de 90°), los ángulos rectos (con sus 90° exactos, con permiso del transportador) los ángulos obtusos (mayores de 90° y menores de 180°), los ángulos llanos (miden 180°, a primera vista parecen una línea), los ángulos cóncavos y convexos (mayor de 180°, pero menor de 360° el cóncavo y convexo, cualquiera entre 0° y 180°) y, por último en esta etapa, el ángulo completo (mide 360°). Hay algunos otros que dependen de los “coles”, los/as “profes” y/o de las ganas de saber más de los/as alumnos/as como pueden ser los ángulos nulos o los ángulos correspondientes.
Tipos de ángulos según su posición
En esta clasificación se trata de ver un ángulo con respecto de otro. De tal manera que se pueden encontrar formando ángulos consecutivos (con un vértice y un ángulo en común), ángulos adyacentes (un tipo de consecutivos que suman entre los dos 180°) y ángulos opuestos por el vértice (dos ángulos que comparten el vértice y dan la sensación de que se pelean por él).
Tipos de ángulos según la suma con otros ángulos
En este caso, habrás visto que ya se tiene en cuenta lo que suman en la categoría anterior, pero en esta se hace más evidente y, como sucede con las personas, nadie ha dicho que un ángulo no pueda ser varias cosas a la vez. De esta forma, tenemos los ángulos complementarios (suman 90°) y los ángulos suplementarios (suman 180°).
Nos reservaremos los ángulos internos, los ángulos externos y los ángulos centrales para dentro de muy poquito… tanto, tanto como que ya llegan con el siguiente apartado.
Las figuras geométricas
Una vez que hemos visto y recordado los contenidos relacionados con ángulos y rectas en Primaria, ya estamos preparados para dar el salto a este nuevo bloque: las figuras geométricas.
En cuanto a las figuras geométricas, debemos comenzar diferenciando entre las formadas por líneas curvas cerradas (círculo y circunferencia) y por líneas poligonales cerradas (polígonos).
Figuras geométricas: ¿curvas cerradas? ¿son la circunferencia y el círculo?
Entre estas dos figuras geométricas siempre hay polémica para determinar quién es quién, cuáles son sus elementos y qué se mide en cada caso. Esperamos que, tras leer las siguientes líneas y practicando después, cualquier persona que haya entrado en Mundo Primaria sepa, sin lugar a duda, diferenciarlas.
La circunferencia es la línea curva que encierra un trozo de un plano, que es el círculo (algo así como el borde de la pizza y todo el relleno). La peculiaridad de la circunferencia, la cual también influye en el círculo, naturalmente, es que todos sus puntos están a la misma distancia de otro que se encuentra en el centro del círculo, razón por la cual recibe ese nombre: centro. Este punto es interesante porque entre sus funciones está ser: el vértice de todos los ángulos centrales de la circunferencia, el punto medio del diámetro y un extremo del radio. Para entender mejor todo esto, acudamos a los siguientes dibujos para comprobar que no es tan difícil y que el “me suena” es más bien “lo sabía”.
¿PERÍMETRO O ÁREA?
No se puede negar que existe el perímetro de un círculo, pues no es otra cosa que la circunferencia. Por lo tanto, diremos que medimos el perímetro de la circunferencia y, ya que el círculo es la superficie interior de esta, le dejamos que se encargue del área.
Así pues, una vez despejadas las dudas sobre estas figuras, le pasamos el relevo a los polígonos.
Figuras geométricas: ¿curvas cerradas? ¿son la circunferencia y el círculo?
En Primaria, se estudian tanto los polígonos regulares (sus lados y ángulos interiores son iguales, por ejemplo: un cuadrado) como los polígonos irregulares (sus lados y ángulos interiores no son iguales, por ejemplo: los triángulos escalenos). En ambos casos, sus componentes se pueden clasificar por sus lados, sus vértices o sus ángulos (aquí están los famosos ángulos interiores y ángulos exteriores). Además, hay que añadir que se aprenden a nombrar por su número de lados.

En el caso de los tipos de triángulos también los nombramos por cómo son sus ángulos (triángulos rectángulos, triángulos acutángulos y triángulos obtusángulos), además de por sus lados (triángulos equiláteros, triángulos isósceles y triángulos escalenos).
El triángulo se estudia con más atención porque es una de las figuras geométricas planas con más curiosidades y salvedades. Si pudiésemos le preguntaríamos a Pitágoras sobre él. Debían de gustarle mucho porque hasta existe un Teorema, el Teorema de Pitágoras, muy útil para descubrir datos de los triángulos rectángulos.
Además de los triángulos, en Primaria, también nos paramos para conocer mejor los tipos de cuadriláteros.
De todas estas figuras y de otras muchas, hallamos sus perímetros y sus áreas igual que sucede con los círculos y las circunferencias; pero, además, en algunas unidades del colegio nos enseñan su simetría (si la tienen) y dónde se encuentra el eje de simetría.
En el apartado que nos queda, vamos a ver unas pincelas de los poliedros que también tienen, a veces, sus propios ejes de simetría; pues, al igual que hay figuras planas que son figuras simétricas, hay cuerpos geométricos que son cuerpos con simetría.