Teorema de Pitágoras
Antes de empezar a hablar sobre el teorema de Pitágoras, y para poder entender de qué se trata, debemos recordar dos cosas:
¿Qué son ángulos rectos?
Veamos:

En el ángulo recto 1 vemos que la medida está expresada directamente y que es de 90º .
Generalmente, los ángulos rectos se marcan completando un pequeño cuadrado, tal como se ve en el ángulo recto 2. En estos casos incluso se omite la medida porque se sobreentiende que es 90º.
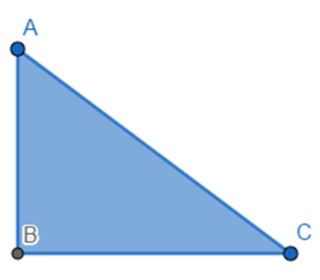
¿Qué es un triángulo rectángulo? ¿Cómo se llaman sus lados?
Veamos algunos ejemplos de triángulos rectángulos:
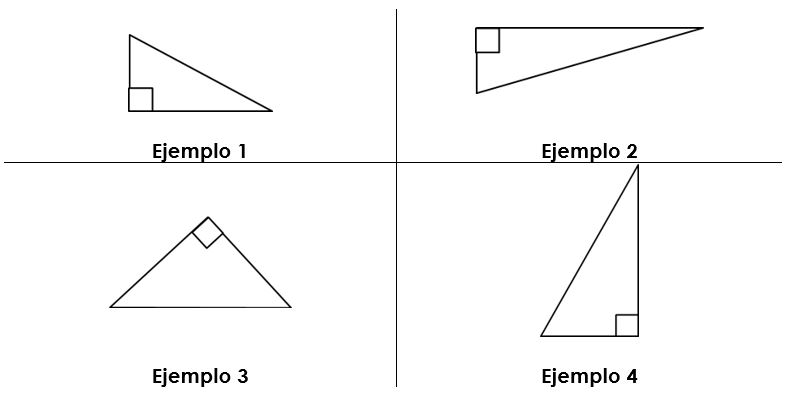
El triángulo que presentamos en el Ejemplo 1 es el más clásico. Es el que aparece más frecuentemente en los libros.
Pero es muy importante que veas bien cómo los demás también son triángulos rectángulos porque poseen un ángulo recto, ¡sin importar la posición en la que se encuentre el triángulo o el ángulo recto!
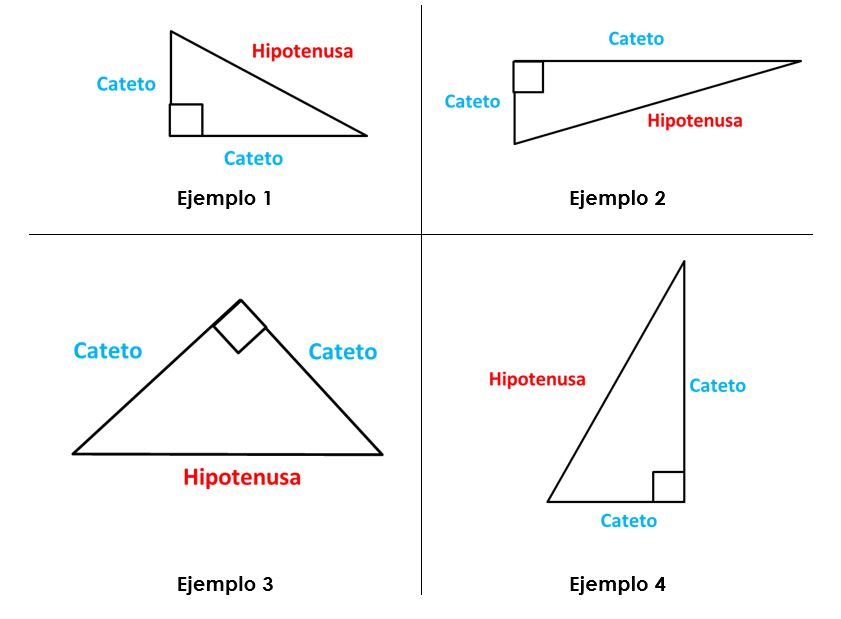
Los lados del triángulo rectángulo se llaman catetos e hipotenusa.
Los catetos son los lados que generan el ángulo recto.
La hipotenusa es el lado opuesto al ángulo recto y es el lado más largo.
Veamos los triángulos anteriores con sus lados identificados:
Ya que conoces los elementos principales que lo forman, veamos de qué trata el teorema de Pitágoras:
Primero tomemos un triángulo rectángulo con las medidas 3, 4 y 5.
Por lo que ya hemos visto, 3 y 4 corresponden a las medidas de los catetos, que son los lados más cortos, y 5 corresponde a la medida de la hipotenusa, que es el lado más largo.
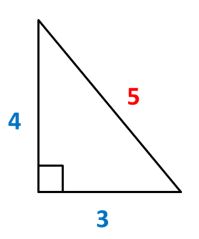
Ahora dibujemos un cuadrado sobre cada uno de sus lados.
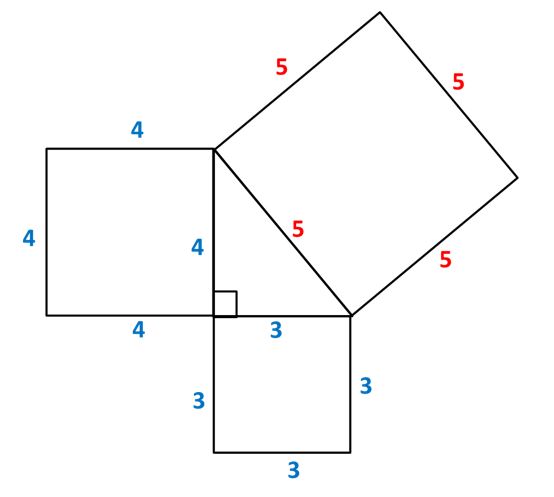
Calculemos el área correspondiente a cada cuadrado.
Recuerda que el área de un cuadrado se calcula multiplicando la medida del lado por sí misma, o elevando la medida del lado al cuadrado, que es lo mismo.
Área del cuadrado = l2, siendo l la medida del lado.
Nos queda entonces lo siguiente:
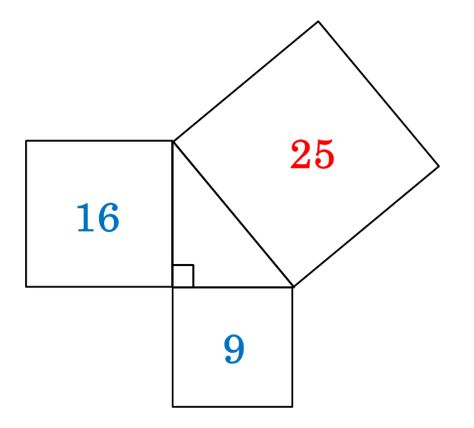
El área del cuadrado del cateto más largo es 16
El área del cuadrado del cateto más corto es 9
El área del cuadrado de la hipotenusa es 25
Fíjate que el área del cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¡Esto que acabamos de enunciar es el teorema de Pitágoras!
Expresado de manera formal, y generalizado para cualquier triángulo, sería:
Teorema de Pitágoras
Dado un triángulo rectángulo cualquiera, la suma de los cuadrados de sus catetos es igual al cuadrado de la hipotenusa.
Si llamamos a y b a los catetos del triángulo rectángulo, y llamamos c a la hipotenusa, se cumple la siguiente igualdad:
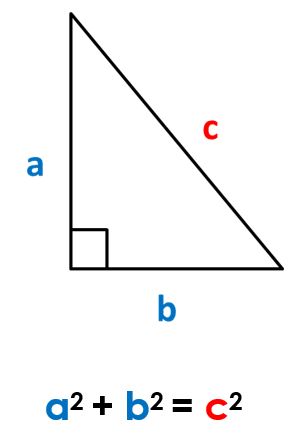
De aquí se deducen las siguientes fórmulas:

Veamos otros ejemplos del teorema.
Planteamiento 1
Sea el triángulo ABC un triángulo rectángulo con las medidas siguientes:
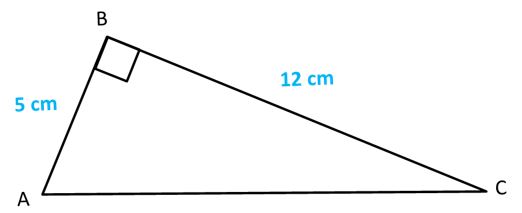
¿Cuánto mide el lado AC?
Solución
- Identificamos las condiciones del planteamiento
Como puedes observar, el triángulo de la figura anterior es rectángulo.
De manera que los lados AB y BC son sus catetos y el lado AC es la hipotenusa.
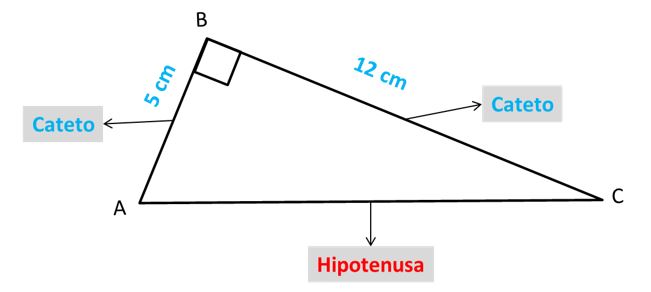
El lado AB mide 5 cm y el lado BC mide 12 cm.
Nos están pidiendo que encontremos cuánto mide la hipotenusa que es el lado AC.
- Aplicamos el teorema de Pitágoras
Sustituimos las condiciones del planteamiento en el teorema de Pitágoras.
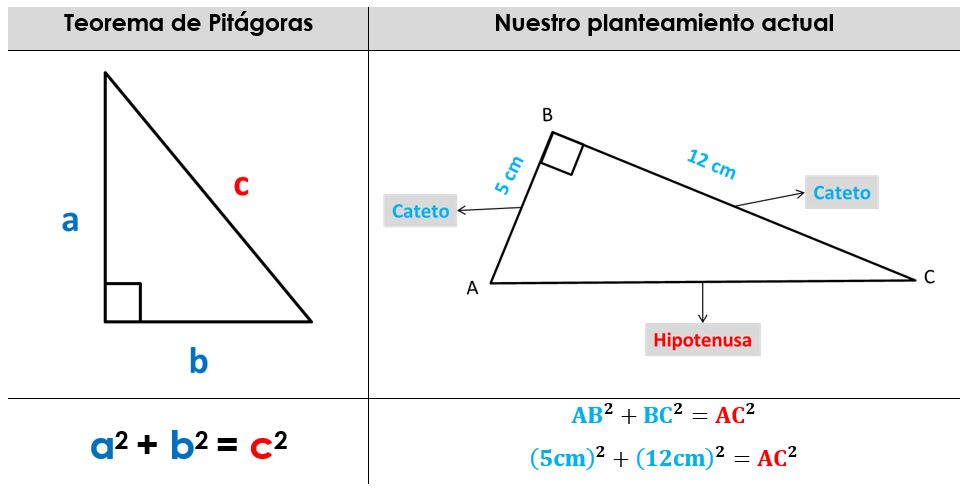
- Resolvemos para conseguir lo que nos piden, que es la medida de AC
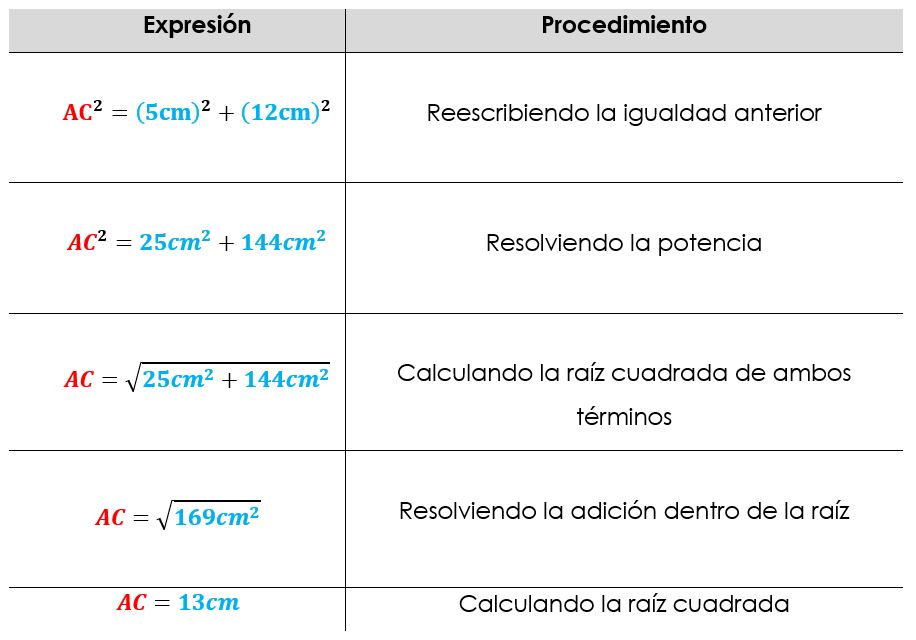
Por tanto, la medida del lado AC es de 13 centímetros.
Planteamiento 2
Observa el siguiente triángulo y calcula la medida faltante:
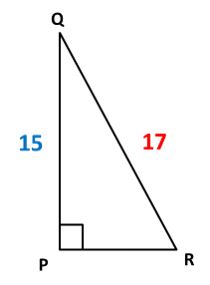
Solución
- Identificamos las condiciones del planteamiento
En este caso tenemos el triángulo rectángulo PQR.
El cateto PQ mide 15, la hipotenusa QR mide17.
Falta la medida del cateto RP, que es lo que nos piden.
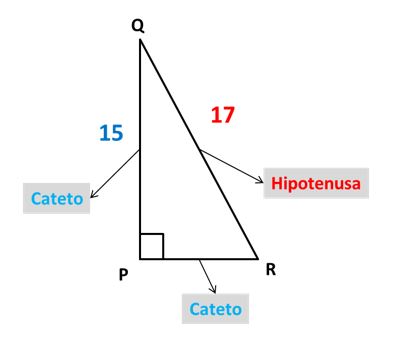
- Aplicamos el teorema de Pitágoras, en este caso calcularemos un cateto, y resolvemos.
Sustituimos las condiciones del planteamiento en el teorema de Pitágoras.
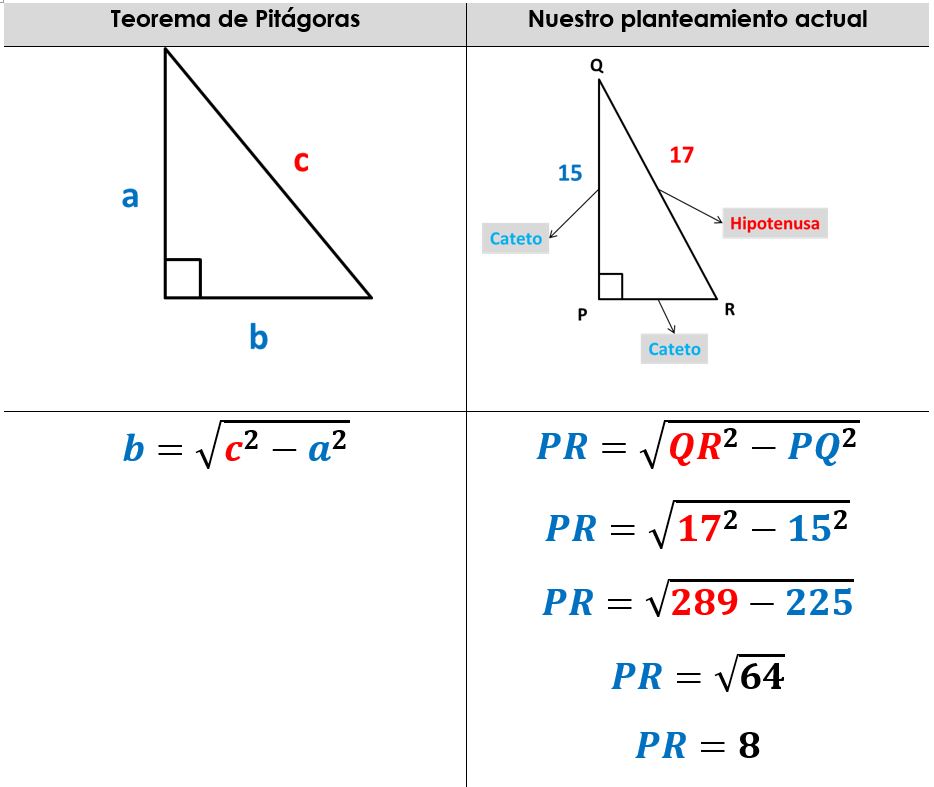
De donde, la medida del cateto PR es igual a 8.
Un poco de historia del teorema de Pitágoras
El origen de lo que hoy se conoce como el teorema de Pitágoras se remonta hasta el Antiguo Egipto. Se tienen indicios que esta civilización conocía y utilizaba a nivel práctico los tripletes pitagóricos.
Un mural egipcio de tres mil años de antigüedad deja ver cómo miembros de las tropas egipcias llevaban una cuerda con 12 nudos equidistantes. Cuando esta cuerda se pone en forma de triángulo con lados de longitud 3, 4, 5 unidades, el triángulo es rectángulo.
Se dice que los egipcios utilizaban este triángulo de forma práctica.
El antiguo Egipto fue una civilización que se formó a lo largo del río Nilo. Egipto fue muy próspero económicamente y esto se debió en gran medida a las periódicas inundaciones que ocasionaba el Nilo en su Delta.
Cuando las aguas del Nilo volvían a su cauce, las tierras quedaban listas para dar inicio a una gran cosecha. Lo único malo era que al inundarse las tierras se perdían los límites de las parcelas. Esto generó que se hicieran muchas mediciones de la tierra, porque año a año se tenían que demarcar las parcelas.
La pregunta era: ¿cómo trazar rectas perpendiculares para demarcar las parcelas que generalmente eran rectangulares?
Esta duda se redujo a la necesidad de construir rectas perpendiculares que le dieran origen a los rectángulos.
¿Qué hicieron los egipcios para resolver este problema?
Fue aquí donde surgió la cuerda con 12 nudos todos a la misma distancia. Los egipcios clavaban el extremo de la cuerda en el suelo y se dedicaban a construir un triángulo en el que sus lados tuvieran 3, 4 y 5 nudos.
Lo primero que realizaban eran 12 nudos en una cuerda todos a igual distancia.

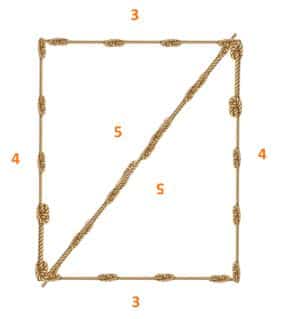
Luego con esa cuerda armaban un triángulo con lados de 3, 4, 5 unidades de longitud. Esta terna determinaba en el interior del triángulo un ángulo recto. De esta manera lograban armar los rectángulos para demarcar las parcelas.
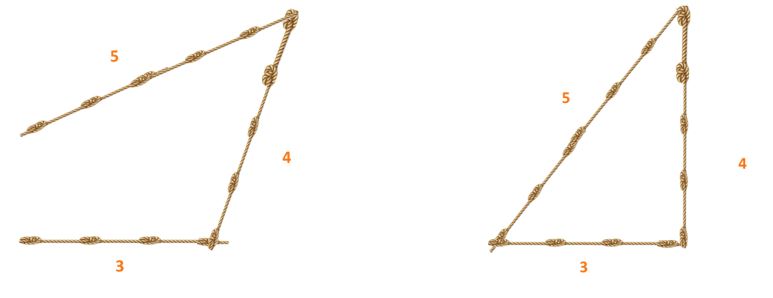
Los encargados de rearmar las parcelas hacían su trabajo con el apoyo de este triángulo sagrado. Fíjate cómo se forma el rectángulo que tanto necesitaban los egipcios.
Sería luego Pitágoras, quien en uno de sus viajes a Egipto descubrió esta propiedad métrica utilizada por los egipcios, quien realizaría la demostración formal. Dando paso así a lo que hoy se conoce con el nombre de Teorema de Pitágoras.
Comprobación geométrica del teorema de Pitágoras
Para visualizar el conocido teorema de Pitágoras, trabajaremos con la idea de los rompecabezas y la abordaremos tal y como lo hizo Platón, quien comprueba este teorema para un triángulo isósceles y rectángulo.
- Lo primero que haremos será construir un triángulo que sea isósceles y rectángulo:
- Ahora dibujaremos un cuadrado sobre cada uno de los catetos. También construiremos un cuadrado sobre la hipotenusa.
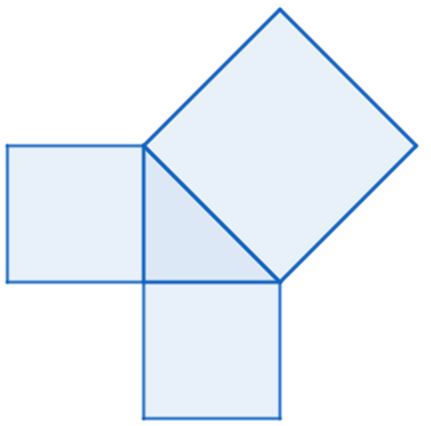
- Ahora trazaremos las dos diagonales de cada uno de los cuadrados que han sido construidos sobre los catetos.
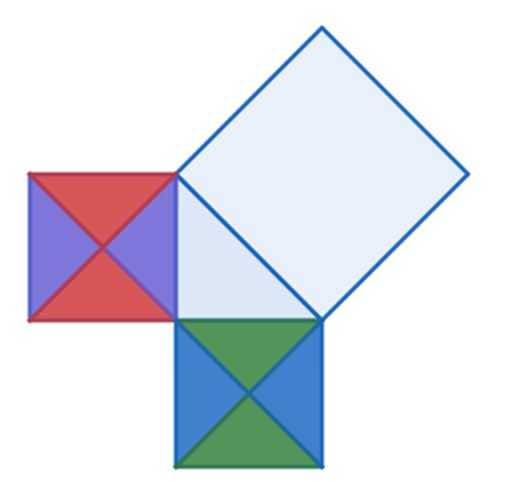
Vemos que la superficie de cada uno de los cuadrados dibujados sobre los catetos, queda cubierta por cuatro triángulos iguales.
- Ahora moveremos, como si de un rompecabezas se tratara, los 8 triángulos de los catetos hacia el cuadrado dibujado sobre la hipotenusa, de tal manera que toda esta superficie quede cubierta.
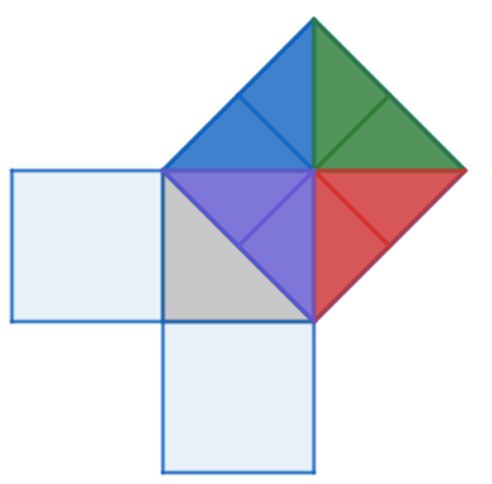
Se puede ver que el área de las superficies construidas sobre los catetos es igual al área de la superficie construida sobre la hipotenusa. A esta relación es a la que se le conoce como el teorema de Pitágoras.
Otra comprobación del teorema de Pitágoras.
Este sencillo rompecabezas comprueba el teorema de Pitágoras en el caso de que la longitud de uno de los catetos sea el doble que la del otro.
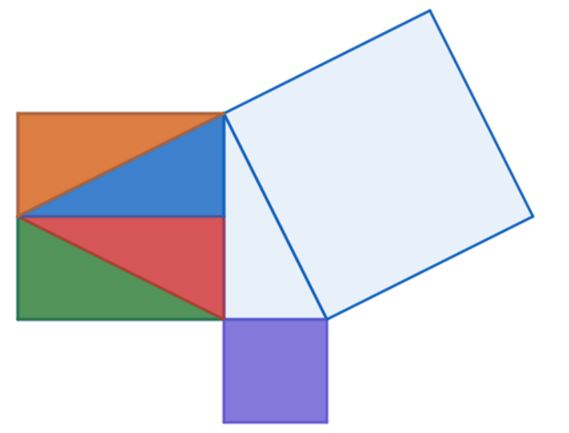
Al reordenar las piezas, se puede visualizar que la suma de las áreas de los cuadrados construidos sobre los catetos es igual al área del cuadrado dibujado sobre la hipotenusa.
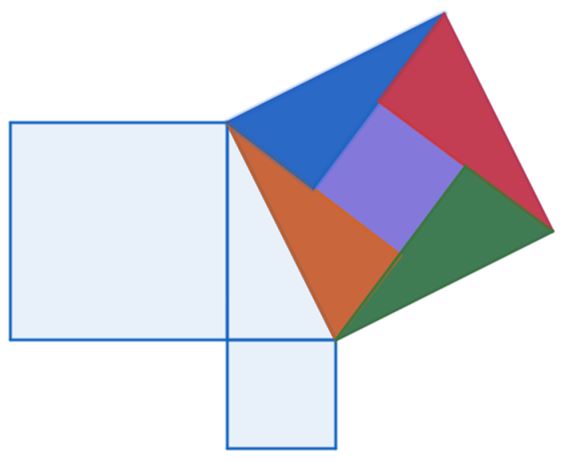
Extendiendo el teorema de Pitágoras
Hemos visto que el teorema de Pitágoras se cumple para cuadrados que se construyen sobre cada uno de los lados de un triángulo rectángulo. ¿Será cierto que el teorema de Pitágoras se cumple para cualesquiera figuras semejantes? Es decir, para figuras que tienen la misma forma, pero no necesariamente el mismo tamaño.
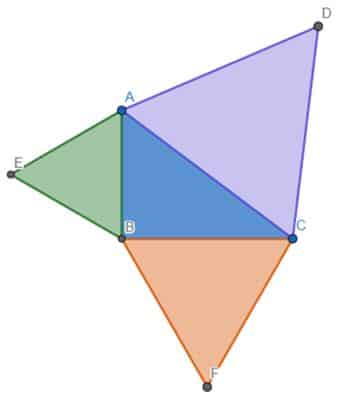
Para visualizar esta nueva idea sobre el teorema de Pitágoras dibujaremos un triángulo rectángulo cuyos lados midan 3 cm, 4 cm y 5 cm.
Ahora dibujaremos tres triángulos equiláteros para ello consideraremos las longitudes 3 cm, 4cm y 5cm del triángulo ABC.
Ahora recortaremos los triángulos equiláteros cuyos lados corresponden a los catetos y la hipotenusa del triángulo ABC.
Toca recortar el triángulo equilátero de lado 3 cm en tres piezas.
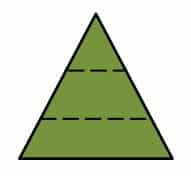
Procedemos a cubrir totalmente el área del triángulo de lados iguales a 5 cm con las piezas obtenidas de los triángulos de 4 cm y 3 cm.
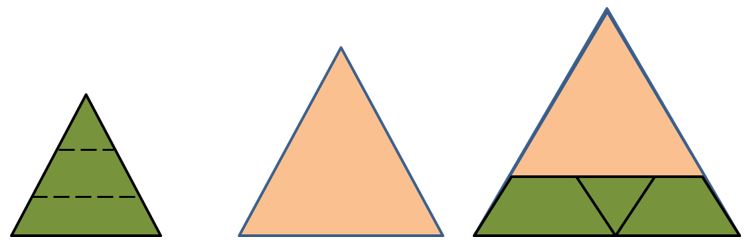
Se observa que la suma de las áreas de los triángulos dibujados sobre los catetos del triángulo ABC es igual al área de la hipotenusa de este mismo triángulo.
De este modo se puede visualizar que el teorema de Pitágoras se cumple para cualesquiera figuras semejantes
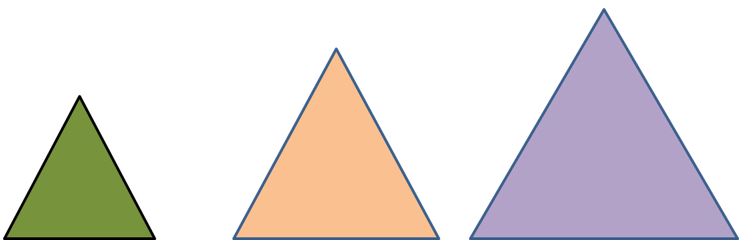
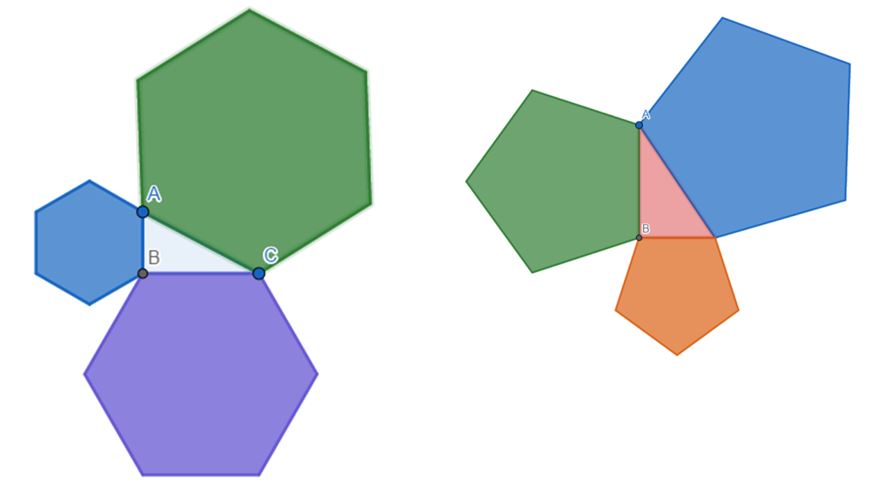
De seguidas les dejamos otros casos de figuras semejantes para los que el teorema de Pitágoras también se cumple.
Algunos problemas aplicados del teorema de Pitágoras
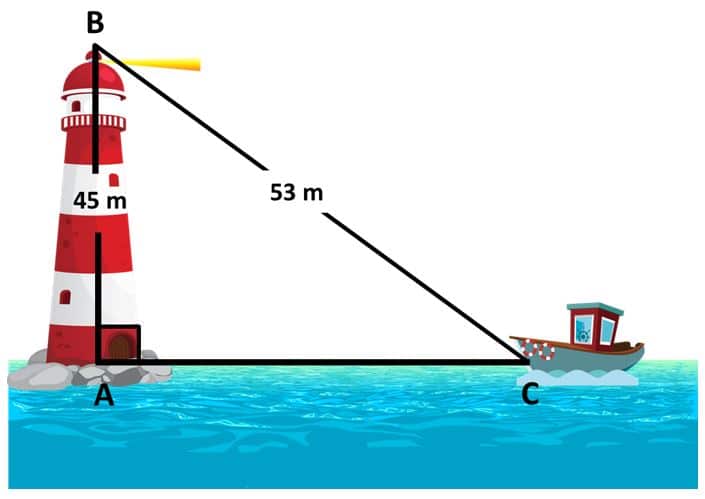
Problema 1: El faro y el bote
Desde la parte más alta de un faro de 45 m de alto se puede observar un bote a 53 m de distancia. Halla la distancia desde el pie del faro hasta el bote.
Solución
Al representar gráficamente la situación nos damos cuenta que la distancia requerida corresponde a uno de los catetos del triángulo rectángulo que se forma con el pie del faro (A), la punta del faro (B) y el bote (C).
La distancia desde el pie del faro hasta el bote se corresponde con el lado AC.
Ahora aplicamos el teorema para hallar la medida del cateto:
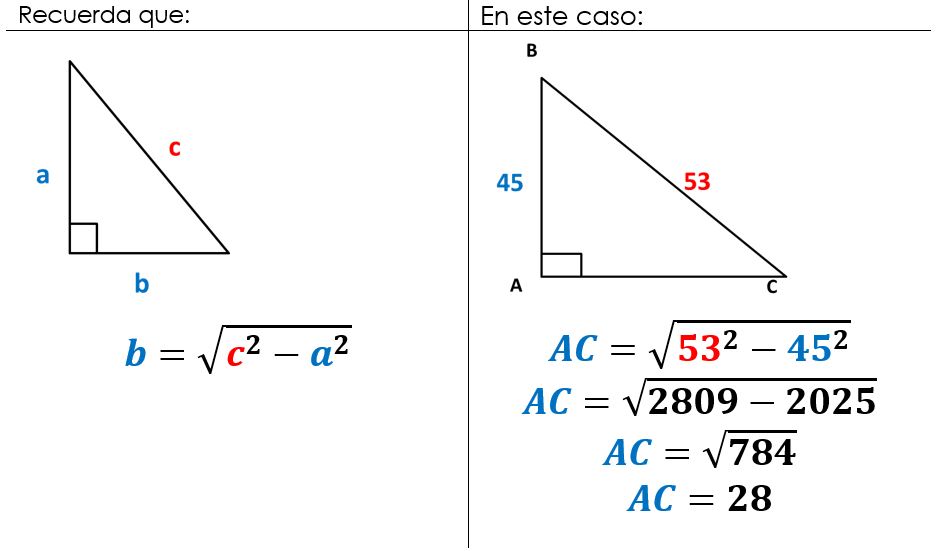
La distancia desde el pie del faro hasta el bote es de 28 metros.
Problema 2: Comprobando si el triángulo es rectángulo
Se tiene el siguiente triángulo:
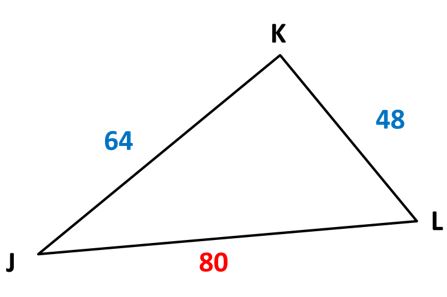
¿Es el triángulo JKL un triángulo rectángulo?
Para responder esto nos apoyaremos en el recíproco del teorema de Pitágoras que dice:
En este caso debe cumplirse que:
JL² = JK² + KL²
Veamos:
80² = 64² + 48²
6400 = 4096 + 2304
6400 = 6400
Como sí se cumple la igualdad del recíproco del teorema de Pitágoras, entonces podemos decir que el triángulo JKL es rectángulo.
Para finalizar, te dejamos unas actividades para practicar lo aprendido:
Selecciona un juego 👇 👇 👇

El triángulo rectángulo

Origen del teorema de Pitágoras

Enunciado del teorema de Pitágoras

Demostración del teorema de Pitágoras

Fórmulas derivadas del teorema de Pitágoras

Aplicación del teorema de Pitágoras en problemas

Cuestionario

El triángulo rectángulo

Origen del teorema de Pitágoras

Enunciado del teorema de Pitágoras

Demostración del teorema de Pitágoras

Fórmulas derivadas del teorema de Pitágoras

Aplicación del teorema de Pitágoras en problemas

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.
