Teorema de Thales
El Teorema de Thales es uno de los teoremas fundamentales en la geometría euclídea. Este teorema tiene muchas aplicaciones prácticas tanto dentro de la matemática como en la vida cotidiana.
En este artículo podrás aprender todo lo que requieres saber sobre este teorema: su definición, un poco de historia, además de aplicaciones y ejercicios resueltos.
- Echa un vistazo: Los números romanos.
Algunos conceptos previos para entender mejor el teorema de Thales
Antes de empezar a hablar sobre el teorema de Thales debemos claridad sobre algunos conceptos fundamentales en geometría:
Rectas paralelas:
Dos rectas son paralelas si no tienen ningún punto común, es decir que jamás coinciden en un punto.
Aquí vemos algunos ejemplos de rectas paralelas:
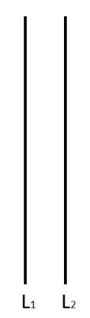
| RECTAS PARALELAS VERTICALES | RECTAS PARALELAS HORIZONTALES |
 |  |
| RECTAS PARALELAS OBLICUAS | |
 | |
En todos los casos anteriores, las rectas L1 y L2 son paralelas.
No importa si son horizontales, verticales u oblicuas, lo importante es saber que las rectas paralelas nunca coincidirán, ni se tocarán.
Rectas paralelas en el entorno
En el ambiente y, en general, en la cotidianidad observamos rectas paralelas en muchas circunstancias.
Veamos algunos de los muchísimos ejemplos de rectas paralelas que hay en nuestro entorno:

Rectas paralelas imaginarias
También podemos trazar de forma imaginaria algunas rectas paralelas a partir de objetos de nuestro entorno.
Fíjate en las siguientes imágenes:
| REPRESENTACIÓN ORIGINAL | REPRESENTACIÓN CON RECTAS PARALELAS IMAGINARIAS |
 |  |
Veamos otro ejemplo:
| REPRESENTACIÓN ORIGINAL | REPRESENTACIÓN CON RECTAS PARALELAS IMAGINARIAS |
 | 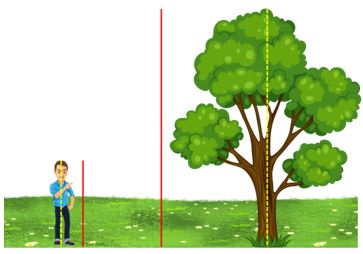 |
Como puedes ver, en la imagen con las rectas paralelas imaginarias los segmentos en rojo son del mismo tamaño que las líneas amarillas puenteadas que van desde el suelo al punto más alto, tanto del hombre como del árbol.
Rectas secantes
Dos rectas son secantes si tienen un punto común. Es decir, si se cortan en un punto.
Todo lo contrario a las rectas paralelas que no tienen punto de corte o coincidencia.
Veamos algunos ejemplos de rectas secantes:
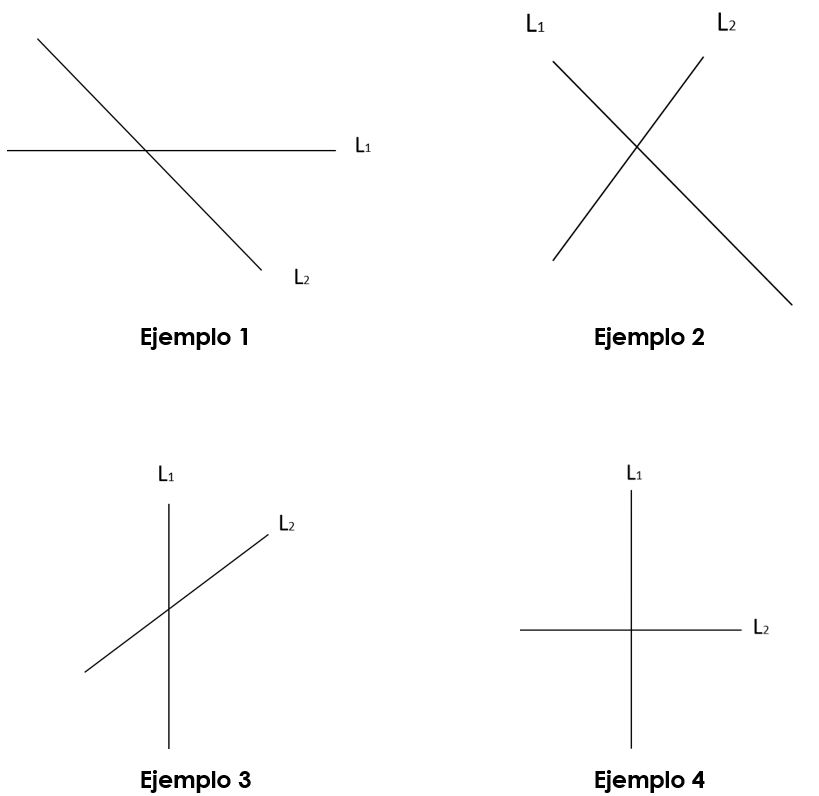
En los cuatro ejemplos anteriores vemos como L1 y L2 son rectas secantes pues tienen un punto en común donde se cortan.
En el ejemplo 4 vemos un caso muy especial de dos rectas secantes que se cortan formando ángulos de 90º. Estas reciben el nombre de rectas perpendiculares.
Rectas paralelas cortadas por rectas secantes
Podemos observar en algunas figuras que las rectas paralelas pueden ser intersectadas por una o más rectas secantes.
Veamos algunos ejemplos:
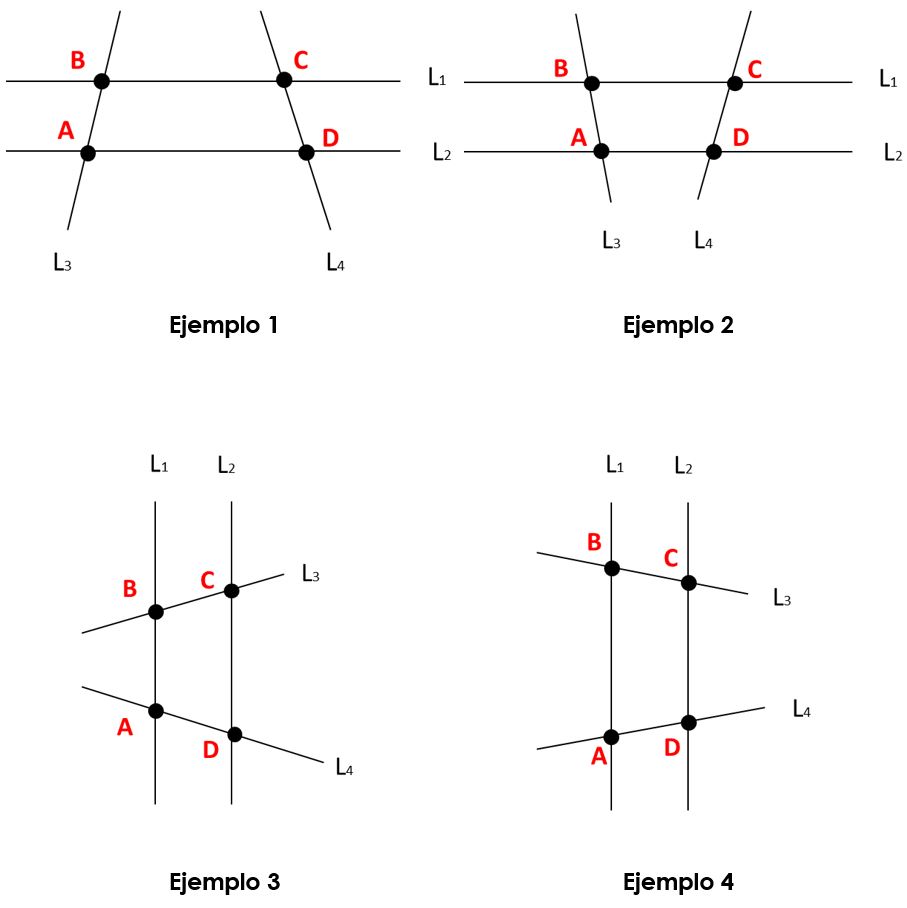
En los ejemplos anteriores vemos como las rectas paralelas L1 y L2 son cortadas por las rectas secantes L3 y L4.
Podemos notar como se forman segmentos de recta que están determinados por los puntos de intersección A, B, C y D.
Tenemos en cada caso los segmentos:
![]()
Proporcionalidad
Para entender el teorema de Thales debemos recordar de qué trata la proporcionalidad.
Esto quiere decir que si una magnitud se duplica, la otra se duplicará, si una magnitud se triplica la otra también se triplicará. De igual manera, si una magnitud se reduce a la mitad la otra magnitud también lo hará a la mitad.
Veamos este primer ejemplo:
Digamos que 1 kg de pechuga de pollo cuesta 6€. Si compramos 2 Kg de pollo pagaremos 12€, pero si compramos ½ Kg de pollo pagaría 6€. Veamos esta relación en la siguiente tabla:

El cociente de proporcionalidad que comentamos anteriormente se obtiene, en este caso, al dividir el precio a pagar entre el número de Kg de pollo que compramos. Veamos:
61= 122= 183= 6
Cuando disminuye también se cumple. Fíjate:
3 ÷ 12 = 61 = 6 y 2 ÷ 13 = 61 = 6
El cociente de proporcionalidad en este caso es 6.
Proporcionalidad en los lados de triángulos semejantes
En Matemática los triángulos que tienen lados proporcionales son semejantes y, recíprocamente, los triángulos semejantes tienen lados proporcionales.
Veamos un ejemplo:
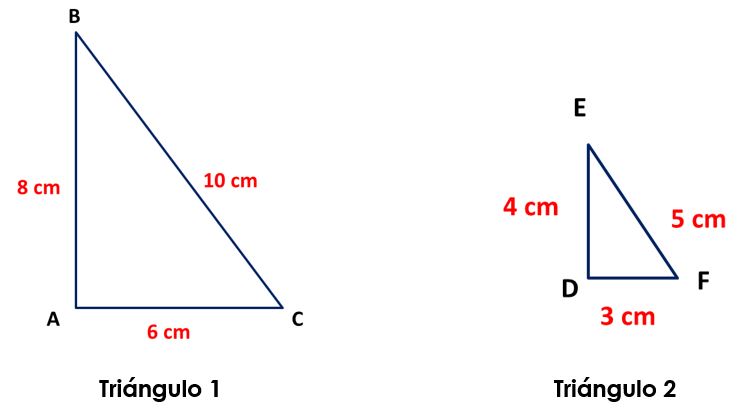
En los triángulos 1 y 2 los lados correspondientes son proporcionales, de manera que los triángulos son semejantes y las medidas de sus lados se relacionan así:

Veamos cuál es su cociente de proporcionalidad:
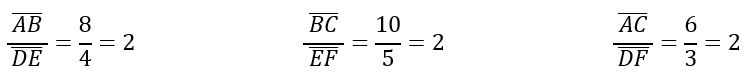
Entonces tenemos que:
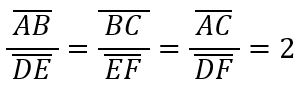
El cociente de proporcionalidad es 2.
Definición del teorema
Los triángulos para la matemática son elementos geométricos de gran importancia. Son muchos los problemas, las modelaciones y visualizaciones que se pueden ejecutar apoyándose en ellos. Las ideas de semejanza, han permitido formular una serie de proposiciones en las que los triángulos y las proporciones son los protagonistas.
En este artículo hablaremos de uno de los teoremas geométricos más conocidos e importantes, como lo es el Teorema de Thales.
Teorema de Thales
Consideremos el triángulo de vértices ABC.
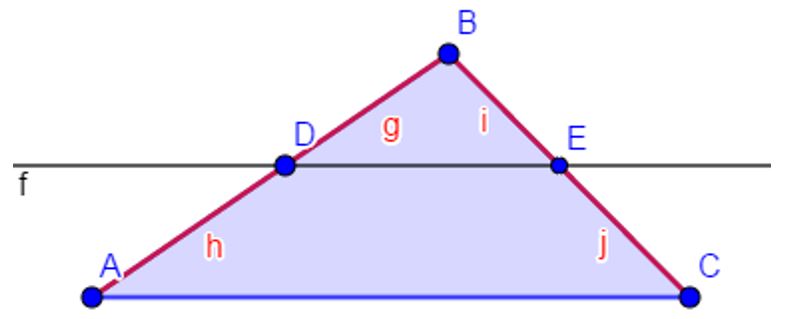
En el triángulo de vértices ABC se tiene que AC // DE . A partir de esta condición de paralelismo estableceremos lo siguiente:
- Los <BDE y <BAC son de igual medida.
- Los <ABC y <DBE son de igual medida.
Por los criterios de semejanza de triángulos y por lo establecido en 1 y 2, podemos afirmar que los ΔABC y ΔDBE son semejantes.
Por lo tanto, se tiene que:
ABDB = CBEB
La relación anterior, es cierta siempre que dos triángulos sean semejantes. Tal y como ocurre con los triángulos ΔABC y ΔDBE representados en la figura.
Si consideramos que las longitudes de los segmentos son las siguientes:
AB = g + h, CB = i + j, DB = g, EB= i
- Entonces, ABDB = CBEB se puede escribir como: g + hg = i + ji.
- Reescribiendo la igualdad se tiene: gg + hg = ii + ji.
- Simplificando: 1 + hg = 1 + ji
- Aplicando la ley de la cancelación: hg = ji
- Transponiendo términos: h.i = j.g
- Transponiendo términos nuevamente: ij = gh
- La expresión anterior es equivalente a: gh = ij
El resultado obtenido es lo que se conoce con el nombre de Teorema de Thales, el cual puede ser expresado como sigue:
De este Teorema se desprende lo que se conoce como el reciproco del Teorema de Thales, que consiste en afirmar que:
Un poco de historia sobre Thales de Mileto y su teorema
Ejemplos de ejercicios resueltos con el teorema de Thales
En este apartado presentamos algunos ejercicios resueltos paso a paso. Veamos el primero:
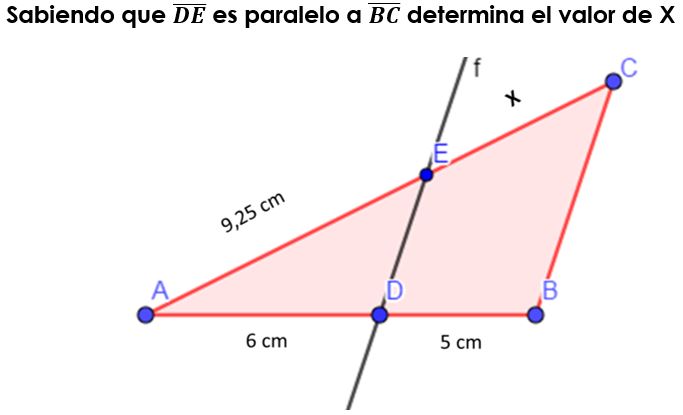
Por el Teorema de Thales sabemos que:
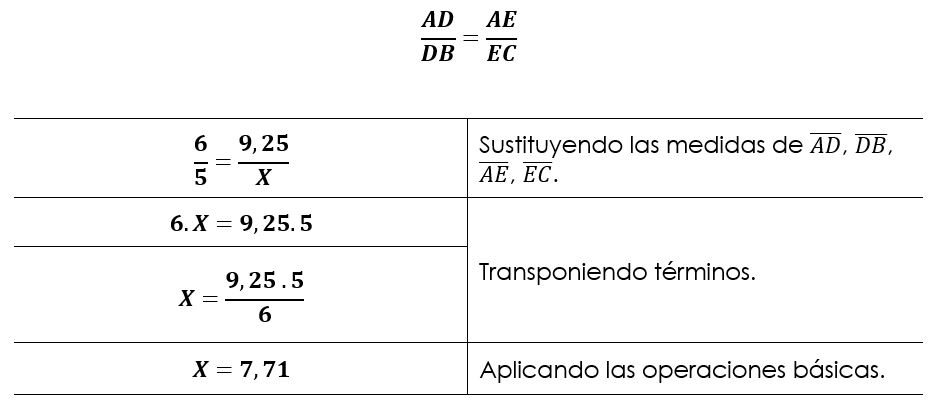
Entonces, el valor de X es igual a 7,71 cm.
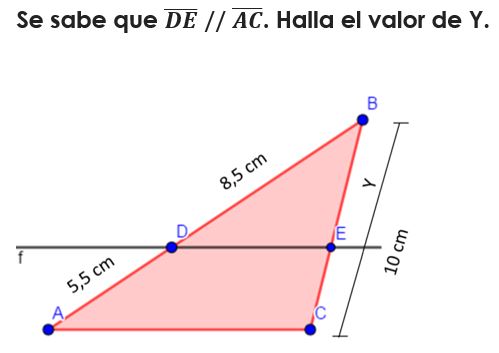
Aplicando el Teorema de Thales se tiene que:

- Sabiendo que FD = 7,5 cm, DA = 10 cm, GE = 6 cm y que o, p, q son rectas paralelas, halla la longitud del segmento EC. ¿Qué teorema has aplicado?
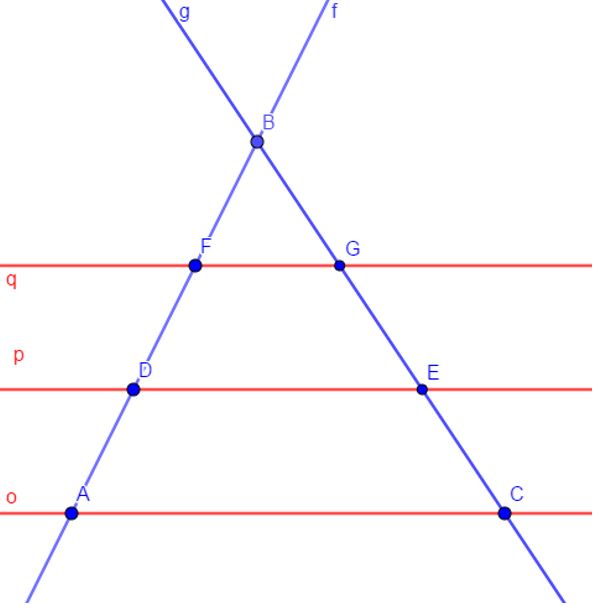
Por el Teorema de Thales se tiene que:

Aplicaciones del Teorema de Thales
La siguiente proposición:
Si una recta intersecta dos lados de un triángulo y divide esos lados en segmentos que son proporcionales entonces la recta es paralela al tercer lado.
Se puede utilizar para dividir cualquier un segmento dado en cualquier número de partes congruentes.
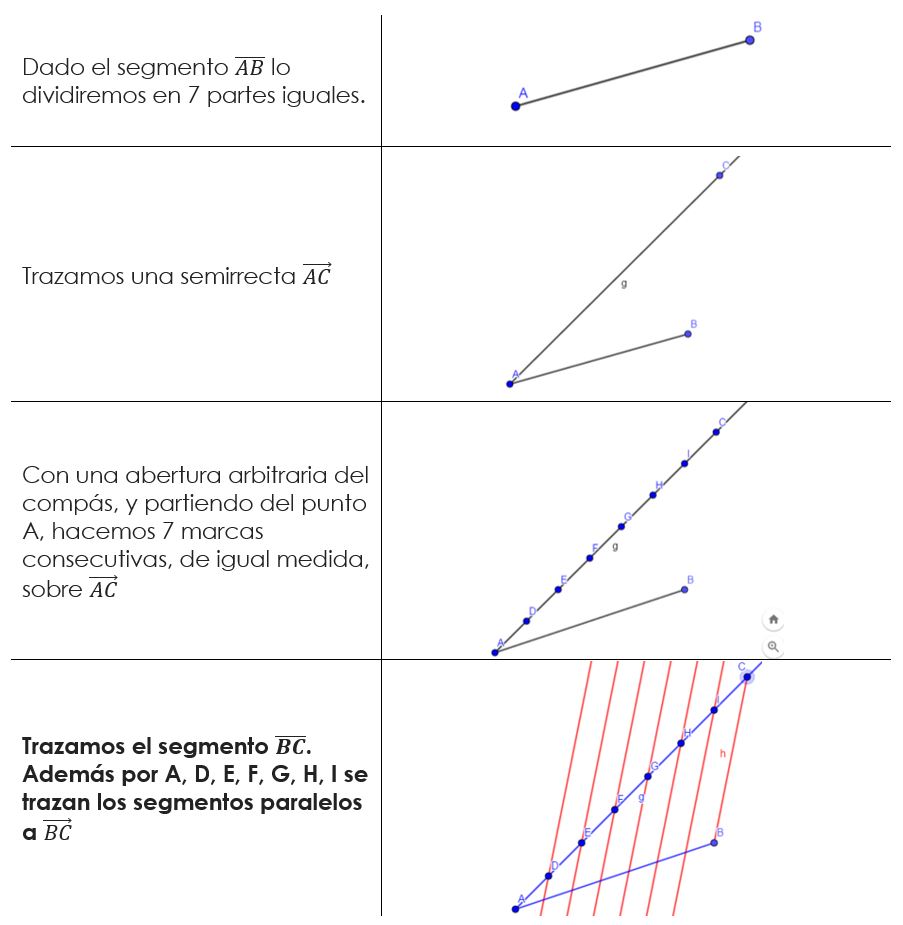
El Teorema que acabamos de formular garantiza que el segmento ha quedado dividido en siete segmentos de igual medida.
Veamos este otro ejemplo de aplicación del teorema de Thales:
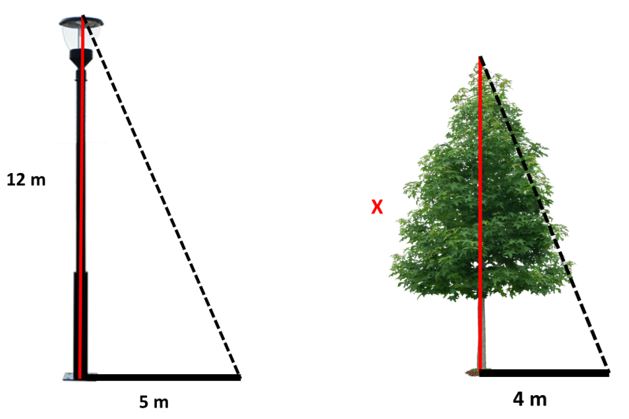
Un poste de luz de 12 m de alto proyecta una sombra de 5m a cierta hora del día. ¿Qué altura tendrá un árbol cercano que proyecta una sombra de 4m a la misma hora?
En este caso podemos aplicar el teorema de Thales porque los triángulos formados son semejantes. Es decir que sus lados son proporcionales.
- De manera que:
12x = 45
- Nos queda:
12 . 5 = 4x
- Luego:
604 = x
- De esto resulta que:
x = 15 metros
- Por último, el árbol mide 15 metros.
Te dejamos unas actividades para que puedas practicar lo aprendido:
Selecciona un juego 👇 👇 👇

Posiciones relativas entre dos rectas

Proporcionalidad

Los triángulos y la proporcionalidad

Teorema de Thales

Aplicación del teorema de Thales 1

Aplicación del teorema de Thales 2

Cuestionario

Posiciones relativas entre dos rectas

Proporcionalidad

Los triángulos y la proporcionalidad

Teorema de Thales

Aplicación del teorema de Thales 1

Aplicación del teorema de Thales 2

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.
