Sucesos seguro, posible e imposible
Nuestra vida está llena de incertidumbre, de eventos que no sabemos con qué certeza ocurrirán.
Por ejemplo, no conocemos de antemano quién ganará el partido de fútbol o qué número saldrá al lanzar un dado. Muchas personas quisieran predecir el futuro para saber qué decisión tomar ante determinada situación.

Entre esas personas que han querido predecir el futuro se encuentran varios matemáticos, quienes con mucha dedicación han ideado formas de medir la posibilidad de ocurrencia de un suceso. Es decir, de calcular la probabilidad de que un evento ocurra.
En este artículo te explicamos qué es un suceso en probabilidad, qué es un suceso posible, imposible y seguro. Además, te decimos cómo puedes calcular la probabilidad de cada uno de estos eventos. No sin antes definir y dar ejemplos de un concepto fundamental como lo es el espacio muestral.
No dejes de leer completo este interesante artículo te será de gran utilidad.
Qué es un espacio muestral
Antes de empezar, debemos definir un término fundamental: espacio muestral.
Veamos tres ejemplos de espacio muestral:
Ejemplo 1
Al lanzar un dado tenemos 6 resultados posibles. Por esta razón el espacio muestral es de 6 elementos.

Ejemplo 2
Se desea sacar, sin ver, una bola roja de una caja que tiene 3 bolas verdes, 2 bolas rojas, 2 bolas azules y 1 bola negra.

BV: bola verde – BR: bola roja – BA: bola azul – BN: Bola negra
Ejemplo 3
Supongamos que lanzamos una moneda tres veces. ¿Cuál será el número de resultados posibles de este experimento?
Podemos contar el número de resultados posibles de este experimento como un conjunto.

También puede ser con un diagrama como el siguiente:
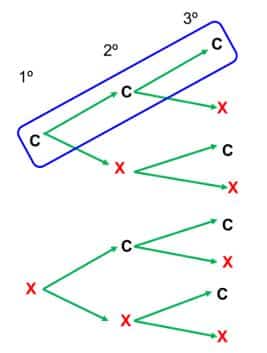
Diagrama de árbol
En este diagrama de árbol hemos representado todos los posibles resultados de este experimento que consiste en lanzar una moneda tres veces.
Lo que aparece encerrado en azul es uno de los posibles resultados. Este sería el caso, en el que en cada uno de los tres lanzamientos sale una cara (C,C,C).
Otro de los resultados sería Cara, Cara, Cruz (C,C,X). También lo hemos marcado en azul para que lo visualices con mayor facilidad.
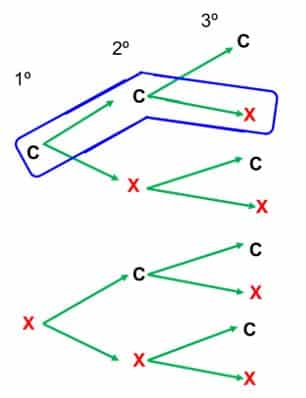
Diagrama de árbol
Siguiendo la dirección de las flechas encontrarás todos los posibles resultados de lanzar una moneda tres veces.
Qué es un suceso en probabilidad
Ejemplo 1
En el experimento anterior, lanzar una moneda tres veces, cualquiera de los posibles resultados es un suceso.
- Por ejemplo, obtener tres caras, al lanzar tres veces la moneda, es un suceso.
- También conseguir una cruz y dos caras, al lanzar tres veces la moneda, es un suceso.
Ejemplo 2
Si lanzamos un dado y una moneda a la vez obtenemos un espacio muestral que se puede representar en un diagrama de árbol.
Veamos:
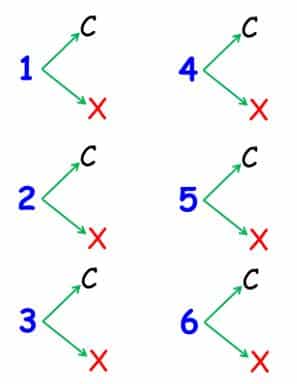
Diagrama de árbol
Al contar encontramos que el espacio muestral de este experimento consta de 12 elementos.
E={1C, 1X, 2C, 2X, 3C, 3X, 4C, 4X, 5C, 5X, 6C, 6X}
Cualquier subconjunto de este espacio muestral es un suceso. Por ejemplo, sacar uno y cara (1C) es un suceso. También es un suceso sacar dos y cruz (2X) o sacar tres y cara (3C).
Cómo calcular la probabilidad de un suceso
La probabilidad de un suceso es un número que nos indica el nivel de certeza que tenemos de que ocurra ese suceso.
Este número que indica la probabilidad de ocurrencia de un suceso es un cociente que se calcula dividiendo el número de casos favorables entre el número de casos posibles, y siempre está entre 0 y 1. Veamos un ejemplo sencillo:
Observa esta ruleta. Vamos a calcular la probabilidad de que al girarla caiga en el color rojo. A esta probabilidad la llamaremos P(rojo).
 | La ruleta está dividida en 12 sectores iguales. Cada sector con un color diferente. ● El número de casos favorables es 1 (hay un solo sector de color rojo). ● El número de casos posibles es 12 (hay 12 colores diferentes). |
| P(rojo) =número de casos favorablesnúmero de casos posibles = 112 = 0,083 | |
| La probabilidad de que al girar la ruleta caiga en el color es 0,083. | |
Qué es un suceso posible y ejemplos
Se dice que la probabilidad de un suceso posible es un número entre 0 y 1.
Ejemplo 1
Sacar un tres al lanzar un dado es un suceso posible porque el 3 forma parte del espacio muestral del experimento. Recuerda que el espacio muestral de lanzar un dado es:
E={1,2,3,4,5,6}
Sacar 3 al lanzar un dado es un suceso posible. Esto es así, porque 3 es parte del espacio muestral del experimento lanzar un dado. La probabilidad de sacar un 3 al lanzar un dado es:
P= 16 = 0,17
Ejemplo 2
Se tienen las siguientes barajas españolas.
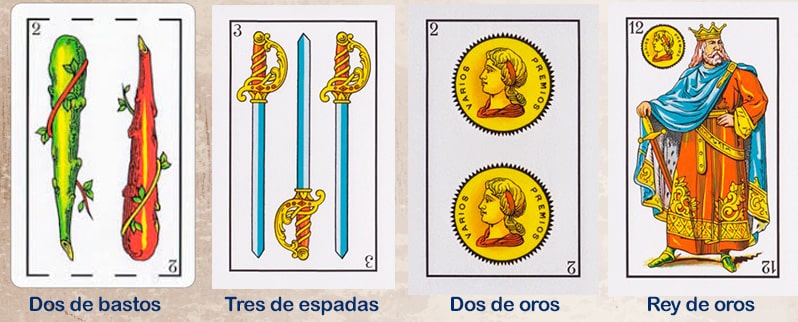
Se desea sacar sin mirar la carta Rey de Oros de este manojo de cartas. ¿Este suceso es posible? ¿Por qué?
Antes de contestar a la pregunta vamos a determinar el espacio muestral de este experimento.
E={Dos de bastos, Tres de espadas, Dos de oros, Rey de oros}
Como vemos el espacio muestral de este experimento consta de 4 elementos.
Como la carta Rey de Oros es parte del espacio muestral, entonces el suceso sacar la carta Rey de Oros es un suceso posible.
En este experimento la probabilidad de sacar la carta Rey de Oros es:
P= 14 = 0,25
Qué es un suceso imposible y ejemplos
Se dice que la probabilidad de un suceso imposible es igual a cero.
Ejemplo 1
Sacar un 8 al lanzar un dado es un suceso imposible, porque el 8 no forma parte de los resultados posibles del experimento de lanzar un dado.
Como ya sabemos el espacio muestral del experimento lanzar un dado es:
E={1, 2, 3, 4, 5, 6}
El 8 no está incluido en el espacio muestral, razón por la que sacar un 8 al lanzar un dado es imposible.
La probabilidad de sacar un 8 al lanzar un dado es:
P= 06 = 0
Ejemplo 2
Sacar una bola negra sin mirar de una caja que tiene 2 bolas rojas, 2 bolas verdes y 1 bola azul es un suceso imposible.

BV: bola verde – BR: bola roja – BA: bola azul
En la caja no hay una bola negra, por lo que el suceso sacar una bola negra sin mirar es imposible en este experimento.
La probabilidad de sacar una bola negra es:
P= 05 = 0
Qué es un suceso seguro y ejemplos
También podemos decir que un suceso seguro es aquel que está formado por todos los resultados posibles que contiene el espacio muestral.
Veamos algunos ejemplos.
Ejemplo 1:

Como puedes observar en la caja hay 6 fichas con los números 2, 4, 6, 8, 10 y 12. Todos son números pares.
Podemos decir que es un suceso seguro que al tomar una ficha obtengas un número par.
La probabilidad de este suceso podemos calcularla así:
P(par)= número de casos favorablesnúmero de casos posibles = 66 = 1
Hay 6 casos posibles, y los 6 casos son favorables.
De aquí podemos deducir que…
Ahora bien, si volvemos a la caja anterior podemos concluir también que escoger una ficha roja es un suceso seguro porque todas las fichas son rojas.
Veamos cómo calcular la probabilidad de ocurrencia de este suceso:
P(roja)= 66 = 1
Como pudiste observar, la probabilidad de tomar una ficha roja es igual a 1, por lo que así también comprobamos que es un suceso seguro.
Ejemplo 2:

Es un suceso seguro que la ruleta caiga en un número menor que 9. Esto es porque todos los números son menores a 9.
Al calcular la probabilidad de este suceso tenemos:
P(n<9)= 88 = 1
Esto también indica que el suceso es seguro, porque la probabilidad de que ocurra es 1.
Ejercicios de sucesos seguros, posibles e imposibles para primaria
En este apartado vamos a desarrollar ejercicios para practicar lo que hemos aprendido sobre sucesos seguros, posibles e imposibles.
Ejercicio 1:

Responde las siguientes preguntas:
- ¿Es un suceso seguro que salga un número par cuando lanzamos el dado? ¿Por qué?
Respuesta:
No es seguro que salga un número par porque hay caras con números impares (1,3 y 5).
Además, al calcular la probabilidad del suceso tenemos:
Número de casos favorables: 3 (Recuerda que hay 3 números pares en el dado: 2, 4 y 6) Número de casos posibles: 6 (El dado tiene 6 caras)
P(par)= número de casos favorablesnúmero de casos posibles = 36 = 12 = 0,5
La probabilidad de que obtengamos un número par no es 1, por lo que también comprobamos así que no es un suceso seguro.
- Cuando lanzamos el dado, ¿es un suceso posible que obtengamos un número menor que 5? ¿Por qué?
Respuesta:
Sí es un suceso posible porque hay 4 caras con números menores a 5 que son 1, 2, 3 y 4.
Esto también podemos comprobarlo al calcular la probabilidad de ocurrencia de este suceso:
Número de casos favorables: 4 (1, 2, 3 y 4 son menores que 5)
Número de casos posibles: 6
P(n<5)= número de casos favorablesnúmero de casos posibles = 46 = 23 = 0,66
En este caso la probabilidad de este suceso es mayor a 0 y menor a 1. Por lo tanto es un suceso posible obtener un número menor a 5 al lanzar el dado.
- ¿Es un suceso imposible obtener el número 7 al lanzar el dado?¿Por qué?
Respuesta:
Sí es un suceso imposible porque los números llegan hasta el 6. De manera que el 7 no está incluido en los resultados posibles de obtener al lanzar un dado tradicional.
Vamos a calcular la probabilidad de que obtengamos un 7:
Número de casos favorables: 0 (no hay 7 puntitos en ninguna cara del dado)
Número de casos posibles: 6
P(n=7)= número de casos favorablesnúmero de casos posibles = 06 = 0
Como vemos, la probabilidad de este suceso es 0. Por lo tanto es un suceso imposible.
Ejercicio 2:
De un mazo de barajas españolas hemos escogido solo las cartas sota, caballo y rey de copas:

- Si escogemos una carta sin mirar, ¿es seguro, posible o imposible que la carta escogida tenga un número mayor que 12?
Es imposible que la carta tenga un número mayor que 12 porque tenemos cartas con los números 10, 11 y 12, (dos menores que 12 y uno igual a 12).
Si queremos calcular la probabilidad de que la carta tenga un número mayor a 12 sería así:
Número de casos favorables: 0 (no hay ningún número mayor a 12)
Número de casos posibles: 3
P(n<12)= 03 = 0
Comprobamos así que el suceso es imposible pues la probabilidad de que ocurra es 0.
- Si alguien toma una carta, sin ver, es seguro que la carta sea de copas.
¿Esto es cierto o falso? ¿Por qué?
Es cierto. Es un suceso seguro que si escogemos cualquier carta de este grupo de barajas, sin ver, sacaremos una de copas.
Esto porque las tres cartas son de ese palo de la baraja.
Para saber la probabilidad de que esto ocurra hacemos lo siguiente:
Número de casos favorables: 3 (las 3 cartas son copas)
Número de casos posibles: 3
P(copa)= 33 = 1
La probabilidad de que sea copa es 1, por eso sabemos también que es un evento seguro.
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇

Algunos términos en probabilidad

Cálculo de la probabilidad de un suceso - 1

Cálculo de la probabilidad de un suceso - 2

Tipos de sucesos - 1

Tipos de sucesos - 2

Algunos términos en probabilidad

Cálculo de la probabilidad de un suceso - 1

Cálculo de la probabilidad de un suceso - 2

Tipos de sucesos - 1

Tipos de sucesos - 2