Sistema Sexagesimal
¿Te has preguntado alguna vez por qué una hora tiene 60 minutos o, por qué una circunferencia completa mide 360°? La respuesta es porque estas medidas de tiempo menores a un día, así como los grados de los ángulos, se miden en un sistema de numeración que no es nuestro Sistema Decimal, que es base 10 y que usamos normalmente para contar. Ese es otro sistema de numeración distinto.

Qué es el sistema sexagesimal
De hecho, el nombre sexagesimal viene de la palabra sexagésimo, que se refiere a cada una de las 60 partes iguales en las que se divide un total.
El sistema sexagesimal es uno de los primeros sistemas posicionales de la historia en los que las cifras del lado izquierdo son mayores que las cifras que están a la derecha, como ocurre con las unidades, decenas y centenas de nuestro sistema de numeración decimal, que es de base 10.
Este sistema fue usado ampliamente en Babilonia (antigua Mesopotamia). Se han encontrado evidencias de su utilización en algunas tablillas de arcilla con escritura cuneiforme, en la que se aprecian registros de diferentes actividades, como las de negocios.

Numeración Babilónica y tablilla cuneiforme usada en la antigua Mesopotamia
De hecho, los babilonios fueron los primeros en dividir la circunferencia en 360 arcos iguales, y le dieron a cada uno el nombre de grado. En el próximo apartado conocerás cómo el sistema sexagesimal se usa en la medición de ángulos en grados, minutos y segundos.
Aplicaciones del sistema sexagesimal
El sistema sexagesimal tiene varias aplicaciones en nuestra vida. Entre las más importantes se encuentran las siguientes:
- La subdivisión del tiempo en unidades menores que un día.
- La medición de ángulos.
Las unidades de tiempo menores que un día son las horas, los minutos y los segundos. Como sabes, una hora tiene 60 minutos, un minuto tiene 60 segundos. Por tanto, una hora tiene 3600 segundos (60 x 60).
Estas unidades de tiempo están basadas en un sistema de base 60, es decir, en el sistema sexagesimal.

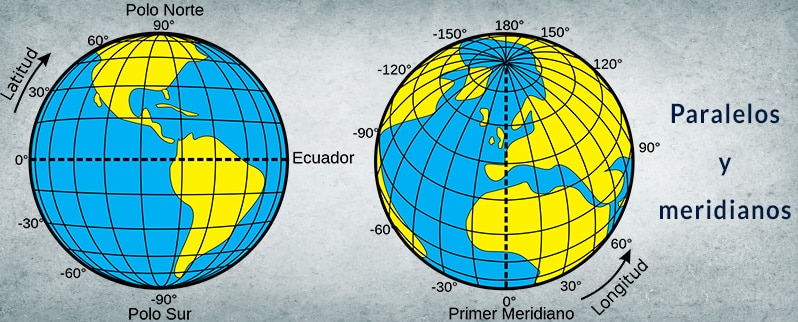
La medición de los ángulos se realiza en grados, minutos sexagesimales y segundos sexagesimales. Estos también son usados al momento de dar las coordenadas exactas de los lugares, es decir, la ubicación exacta de un lugar en el globo terráqueo.
Para ello se usan la latitud (Norte-Sur), que está relacionada con los paralelos, y la longitud (Este-Oeste), relacionada con los meridianos.
- Por ejemplo, las coordenadas de Madrid son:
- Latitud: 40°24′59″ N (40 grados, 24 minutos, 59 segundos al Norte).
- Longitud: 3°42′09″ O (3 grados, 42 minutos, 9 segundos al Oeste).
- Y las coordenadas de Caracas son:
- Latitud: 10°29′16″ N (10 grados, 29 minutos, 16 segundos al Norte).
- Longitud: 66°52′45″ O (66 grados, 52 minutos, 45 segundos al Oeste).
Ángulos en el sistema sexagesimal
Como ya te hemos dicho el sistema sexagesimal se aplica principalmente para la medida de ángulos y también en la medida del tiempo.
En el sistema sexagesimal la unidad de medida de los ángulos es el grado.
Un grado es lo que resulta de dividir la circunferencia en 360 partes iguales. Es así como la mitad de la circunferencia es un ángulo llano que mide 180º y la cuarta parte de la circunferencia es un ángulo recto cuya medida es 90º.
Observa:
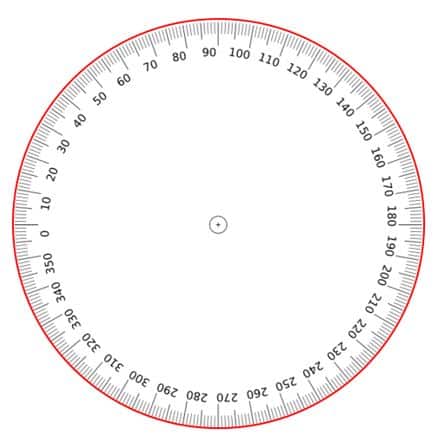 | |
| Circunferencia dividida en 360 partes iguales | |
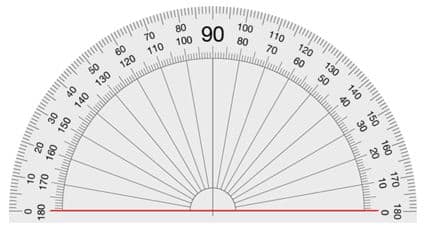 | 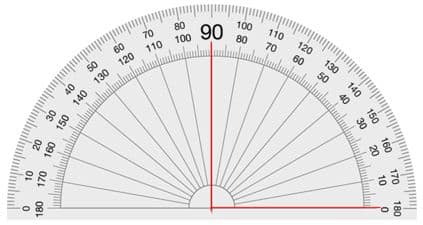 |
| El ángulo llano mide 180º | El ángulo recto mide 90º |
Cada uno de los 360º de una circunferencia se puede dividir en unidades más pequeñas.
En el caso del sistema sexagesimal cada grado es subdividido en 60 partes iguales.
Es así como cada grado se divide en 60 minutos (1º = 60’) y cada minuto en 60 segundos (1 min = 60’’).
- Un grado (1º) → 60 minutos (60′)
- Un minuto (1′) → 60 segundos (60″)
- Un grado (1º) → 3.600 segundos (3.600″)
El siguiente esquema te puede ayudar a entender estas igualdades y cómo pasar de unas medidas a otras:
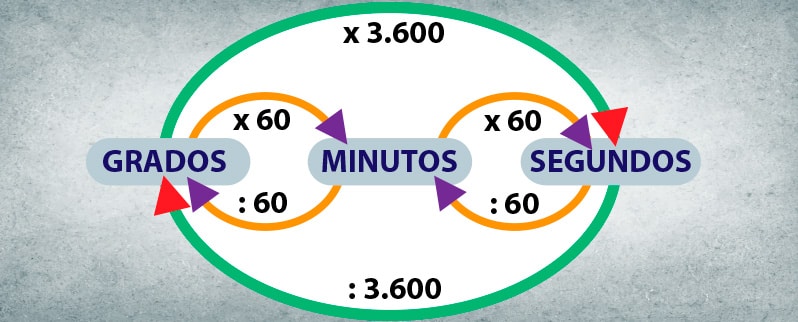
Por ejemplo:
- 62º 46’ 58’’ hace referencia a un ángulo cuya medida es 62 grados, 46 minutos y 58 segundos.
- Escribir 25º 0’ 0’’ es equivalente a 25º.
Formas de escribir los ángulos (compleja o incompleja)
Un ángulo cuya medida está dada en grados, minutos y segundos, se dice que está expresado en forma compleja, mientras que si se escribe con una sola clase de unidades (grados, minutos o segundos), entonces se dice que es una medida simple o incompleja.
Mira estos ejemplos:
| Ejemplos de Forma Compleja | Ejemplos de Forma Simple o Incompleja |
| 72º 25’ 41’’ | 38º |
| 28º 33’ 19’’ | 17’’ |
| 5º 44’ | 23’ |
| 56’ 53’’ | 12º |
Cómo sumar ángulos
Para sumar medidas de ángulos expresadas en grados sexageximales debemos colocar de forma vertical y ordenada cada uno de los sumandos.
Es decir, colocamos los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos. Veamos dos ejemplos:
- Si queremos sumar 52º 36’ 28’’ más 45º 25’ 12’’, procedemos de la siguiente manera:

- El resultado de sumar 52º 36’ 28’’ + 45º 25’ 12’’ = 97º 51’ 40’’
- Sumemos ahora 35º 44’ 58’’ más 72º 52’ 23’’.
 En este caso los segundos suman más de 60, por lo que dividimos 81 entre 60.
En este caso los segundos suman más de 60, por lo que dividimos 81 entre 60.
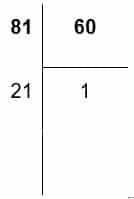
- El resto de esta división, en este caso 21, son los segundos. Mientras que el cociente se lo añadiremos a los minutos.

- Con la unidad que agregamos nos quedan 97 minutos que es mayor que 60, por lo que dividimos 97 entre 60.
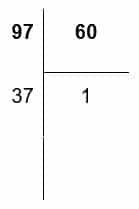
- El resto de la división, que es 37, son los minutos y el cociente, que es 1, se lo agregamos a los grados. Nos queda lo siguiente:

- El resultado de sumar 35º 44’ 58’’ + 72º 52’ 23’’ es 108º 37’ 21’’
- Otra forma de resolver esta suma sería la que se muestra en la siguiente imagen:
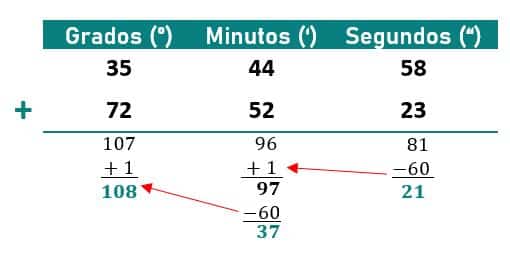
Conversiones de medidas de tiempo en el sistema sexagesimal
Para convertir medidas de tiempo en el sistema sexagesimal debemos recordar algunas equivalencias:
- Una hora → 60 minutos
- Un minuto → 60 segundos
- Una hora → 3.600 segundos
Como en el caso anterior este esquema te puede ayudar a ver las correspondencias entre las diferentes medidas:
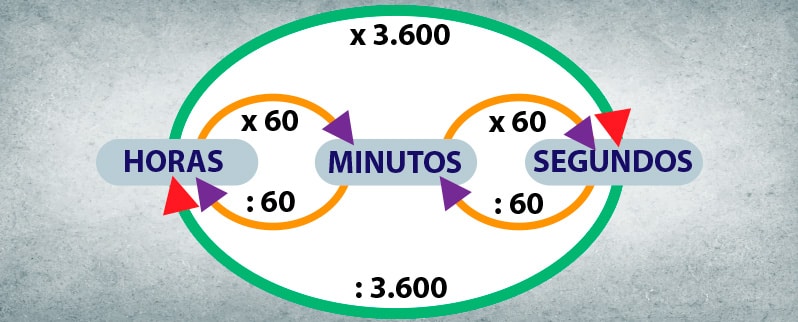
Teniendo esto presente, podemos convertir las medidas de tiempo en el sistema sexagesimal.
Convertir a horas
Para convertir a horas los minutos y los segundos debemos hacer lo siguiente:
- Convertimos los segundos en minutos dividiendo entre 60.
- Sumamos los minutos que obtuvimos con los que nos habían dado.
- Convertimos los minutos obtenidos en el procedimiento anterior en horas dividiendo entre 60.
- Sumamos las horas obtenidas con las que nos habían dado.
Veamos un ejemplo:
Convertir 2h 45min 30s a horas
- Primero vamos a convertir los 30 segundos a minutos. Para ello dividimos 30 entre 60, nos queda así:

- Tenemos que 30 segundos son equivalentes a 0,5 minutos.
- Ahora vamos a sumar los minutos que obtuvimos con los que nos habían dado:
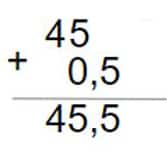
- Tenemos 45,5 minutos.
- Convertimos los minutos en horas dividiendo por 60. Nos queda así:
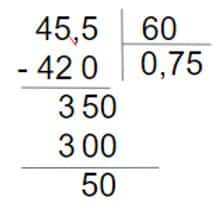
- Tenemos 0,75 horas, aproximadamente.
- Sumaremos ahora las horas que obtuvimos con las que nos habían dado. Nos queda así:
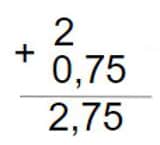
- Podemos decir que 2h 45min 30s es equivalente a 2,75 horas, aproximadamente.
Convertir a minutos
Para convertir a minutos seguimos los siguientes pasos:
- Convertimos las horas en minutos multiplicando por 60.
- Luego, convertimos los segundos en minutos dividiéndolos por 60.
- Por último, sumamos los minutos obtenidos en los dos pasos anteriores con los minutos que nos habían dado.
Por ejemplo, convierte 5h 32min 45s a minutos
- Primero convertimos las horas a minutos multiplicando por 60.
5 x 60 = 300
- Tenemos 300 minutos.
- Ahora convertimos los segundos en minutos dividiendo por 60.

- Tenemos 0,75 minutos.
- Por último, sumamos los minutos que obtuvimos en los dos procedimientos anteriores con los minutos que nos habían dado:
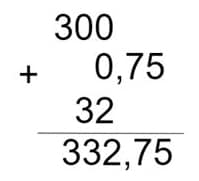
- Concluimos entonces que 5h 32min 45s es equivalente a 332,75 minutos.
Convertir a segundos
Para convertir a segundos debes hacer lo siguiente:
- Pasar las horas a segundos multiplicando por 3.600.
- Pasar los minutos a segundos multiplicando por 60.
- Sumar los segundos obtenidos de los procedimientos anteriores con los segundos que te dieron inicialmente.
Veamos esto con un ejemplo:
Convertir 3h 12min 23s a segundos.
- Empezamos convirtiendo 3 horas a segundos, para lo cual multiplicamos por 3.600.
3 x 3.600 = 10.800
- Tenemos 10.800 segundos.
- Ahora convertimos los minutos en segundos multiplicándolos por 60.
12 x 60 = 720
- Tenemos 720 segundos.
- Por último, sumamos los segundos obtenidos en los dos procedimientos anteriores con los segundos que nos dieron. Nos queda así:
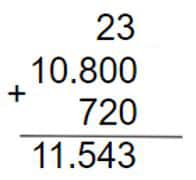
- Podemos decir que 3h 12min 23s es equivalente a 11.543 segundos.
Operaciones en el sistema sexagesimal
Dependiendo de la situación o el problema con el que te enfrentes, es probable que necesites hacer cálculos y transformaciones en el sistema sexagesimal. En este apartado te decidimos cómo realizar este tipo de operaciones de forma rápida y efectiva.
Pasando de una medida compleja a una simple o incompleja
Para transformar una medida compleja en una simple, hay que expresarlas todas en la unidad que queremos obtener y posteriormente sumarlas.
Veamos un ejemplo:
- Vamos a transformar la medida compleja 6º 25’ 32’’a una incompleja en segundos.
- En primer lugar transformamos los 6º a segundos.
- Lo hacemos multiplicando 6 x 3600 = 21.600 segundos.
- En segundo lugar transformamos 25’ a segundos.
- Para ello, multiplicamos 25 x 60 = 1.500 segundos.
- En tercer lugar sumamos todas las medidas expresadas en segundos.
- Esto es, 21.600’’ + 1.500’’ + 32’’ = 23.132’’.
- Concluimos, que 6º 25’ 32’’ = 23.132’’
Pasando de una medida incompleja (o simple) a una compleja.
Para transformar una medida incompleja a compleja debemos tener en cuenta que:
- Hay que dividir cuando vamos de una unidad más pequeña a otras más grandes.
- Y hay que multiplicar cuando se pasa de unidades más grandes a otras más pequeñas.
Veamos varios ejemplos:
- Transformemos la medida incompleja 8.365 segundos a una compleja.
- En este caso vamos de segundos a minutos y grados. Es decir, de una unidad más pequeña a otra más grande.
- Por lo tanto, dividimos 2.365 entre 60.
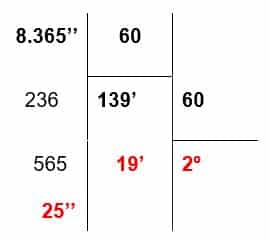
- Luego de hacer la división, hay que tener en cuenta que:
- En el último cociente quedan representados los grados, en el penúltimo residuo los minutos y en el último residuo los segundos.
- Entonces, la transformación quedaría así: 2º 19’ 25’’ = 8.365’’ .
- En este ejemplo fuimos de una unidad más pequeña (segundos) a otras más grandes.
- Convirtamos la medida incompleja 20,5º a una compleja.
- En este caso vamos de grados a minutos. Es decir, de una unidad más grande a otra más pequeña. Entonces, multiplicamos por 60 la parte decimal de la medida. Veamos:
20,5º = 20º + 0,5º
- Como lo queremos convertir a minutos es la parte decimal de la medida simple, multiplicamos 0,5 x 60 = 30. Por lo tanto:
20,5º = 20º 30’
- En este ejemplo nos movimos de una más grande a otra más pequeña.
- Convirtamos la medida simple 6.552 segundos a una compleja
- En este ejemplo vamos de segundos a minutos y grados. Es decir, de una unidad más pequeña a otras más grandes.
- Por esta razón dividimos 6.552’’ entre 60. El resultado de esta división lo dividimos nuevamente entre 60. Y así sucesivamente hasta lograr que el cociente que resulta sea menor que 60.
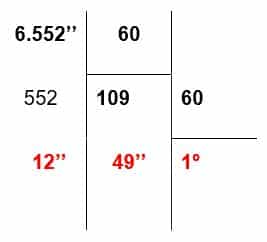
- Una vez hecha la división, hay que tener en cuenta que:
- En el último cociente quedan representados los grados, en el penúltimo residuo los minutos y en el último residuo los segundos. Entonces, la transformación quedaría así:
1º 49’ 12’’ = 6.552’’
- En este ejemplo fuimos de una unidad más pequeña (segundos) a otras más grandes.
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇

Definición del sistema sexagesimal

Características del sistema sexagesimal

Aplicaciones del sistema sexagesimal

Conversión de unidades del sistema sexagesimal

Suma y resta con expresiones complejas

Paso de complejo a incomplejo y al revés

Definición del sistema sexagesimal

Características del sistema sexagesimal

Aplicaciones del sistema sexagesimal

Conversión de unidades del sistema sexagesimal

Suma y resta con expresiones complejas

Paso de complejo a incomplejo y al revés
 En este caso los segundos suman más de 60, por lo que dividimos 81 entre 60.
En este caso los segundos suman más de 60, por lo que dividimos 81 entre 60.