Sistema de longitud
En este artículo conocerás acerca de la medida, específicamente aprenderás sobre la forma en que se mide la longitud de los objetos.

Cinta métrica usada para medir objetos
La longitud es una de las medidas más usadas en nuestra vida diaria. Esto es porque conocer la longitud de los objetos nos permite saber, por ejemplo, como de lejos queda tu escuela de tu casa, cuánto has crecido en el último año, la distancia entre la Tierra y el Sol, el diámetro de un átomo y otras muchas cosas más.
¿Qué es la longitud?
El término longitud proviene del vocablo longitudo, o longitudinis, perteneciente al latín y con el mismo significado que en español.
Algunos ejemplos del uso de la longitud en la vida diaria son:
- Distancia entre dos lugares
Veamos la distancia en línea recta entre Torrejón de Ardoz y Las Rosas de Madrid (ambas en Madrid, España).
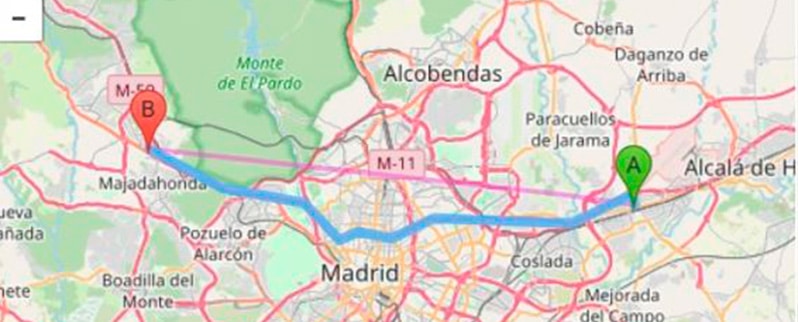
En la figura Torrejón de Ardoz está marcado con la letra A, mientras que Las Rozas de Madrid está marcada con la letra B.
La distancia en línea recta entre ambos lugares es de 33,70 km.
Imagina que tomamos un helicóptero, por ejemplo, y volamos de una ciudad a otra, esa distancia es la que recorreremos.
La distancia de la ruta en coche entre ambos lugares es de 48 km.
- Altura de una persona
Esto es cuando por ejemplo nos mide el médico al ir a una consulta. O cuando nos medimos en casa para saber cuánto has crecido. Incluso en algunos parques hay una longitud mínima para subir a ciertos juegos.

- Ancho y largo de un objeto
Muchas veces necesitamos saber cuánto mide un objeto para saber si cabe en el lugar donde queremos colocarlo. Por ejemplo, debemos saber el ancho de una cama para saber si cabe en nuestra habitación.

La longitud en la física
En física existe lo que se conoce como longitud de onda. La longitud de onda aparece en las ondas periódicas y es la distancia entre dos puntos a partir de los que la onda se repite. Este tipo de longitud se representa con la letra griega lambda (λ).
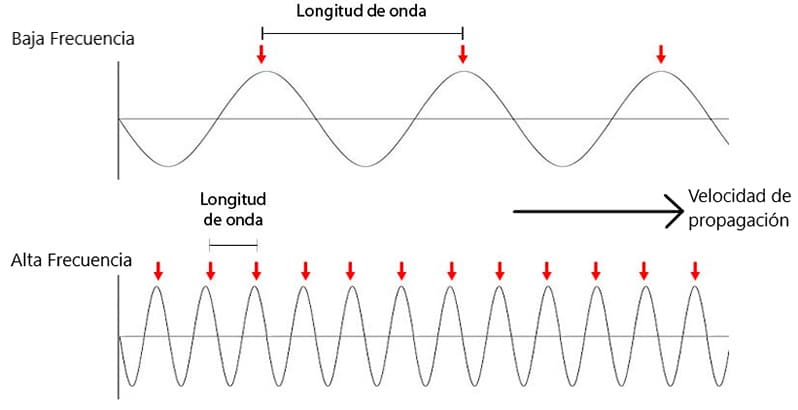
Longitud de onda en ondas de alta y baja frecuencia – Tomado de: esero.es
Longitud y latitud
Para ubicar cualquier lugar en nuestro planeta utilizamos las coordenadas que se refieren a la longitud y a la latitud.
- La latitud se refiere a la distancia que hay entre un paralelo y el Ecuador de la Tierra. Se mide en grados y va desde 0º, correspondientes al ecuador, hasta 90º, correspondientes a los polos.
- La longitud es la distancia que hay entre un meridiano y el meridiano de Greenwich. Se mide en grados que van desde 0º, que sería el meridiano de Greenwich, a los 180º que sería el meridiano que está en la posición opuesta a Greenwich.
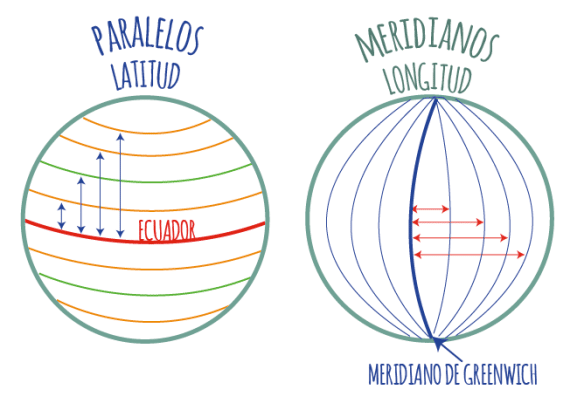
Paralelos y meridianos – Tomado de: materialescienciassociales.com
Con la ficha que aparece a continuación podrás reforzar lo visto sobre el concepto de longitud.
¿Cómo se mide la longitud?
Antes de empezar a explicar cómo se mide la longitud veamos la necesidad de medir longitudes que ha tenido el ser humano, y algunas de las unidades de medida que ha empleado.
Desde hace mucho tiempo los seres humanos tuvimos la necesidad de medir. En la antigüedad las distancias entre las ciudades se medían por los días de viaje que tomaba ir de una ciudad a otra. Pero como esto no era aplicable a las situaciones del día a día, las personas empezaron a usar las partes del cuerpo para medir.
Es así como se usaban medidas como el pie, la pulgada, la braza, entre otras. Estas medidas son las llamadas medidas no convencionales.
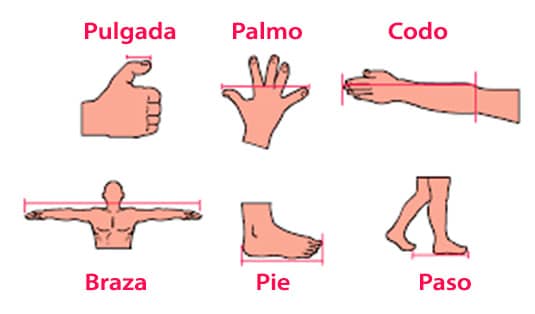
Mira este vídeo para repasar las medidas no convencionales:
¿Cómo se mide?
Medir es comparar un objeto con una unidad de medida. Por ello, para medir algo debemos determinar cuántas veces “cabe” esa unidad de medida en el objeto que estamos midiendo.
Para entender mejor el proceso de medir, vamos a usar una medida no convencional. Esto te ayudará a entender mejor al salirnos de los patrones tradicionales de medida.
Veamos cuál es la medida en pasos del largo de la ventana de este piso.

Como puedes ver el largo de la ventana es de 6 pasos. Estos fueron medidos con el paso de una persona adulta.
Ahora bien, si son los pasos de un niño pequeño, por ejemplo, los que usamos para medir, lo más probable es que sean más pasos.
Esta discrepancia en el uso de las medidas no convencionales dio origen al acuerdo internacional de las diferentes medidas de longitud que vemos hoy en día como el metro, el centímetro, el kilómetro, entre otras.
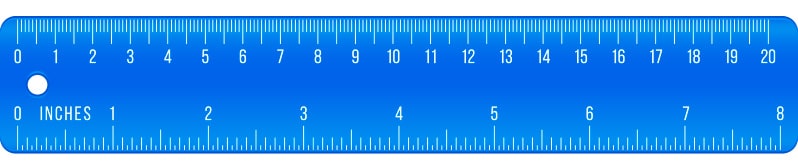
Regla graduada
Y a diferentes instrumentos de medición de la longitud como la regla graduada que usan a diario los niños en el colegio.
Veamos cómo se mide con una regla graduada
Para medir un objeto con la regla graduada debemos seguir los siguientes pasos:
- Ubica los centímetros en la regla. Algunas reglas tienen dos tipos de unidades de medida: centímetros y pulgadas (inches en inglés).
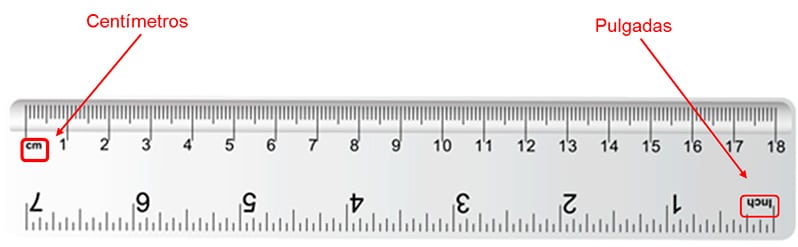
- Los centímetros son los nombrado como «cm» y los que tienen menor distancia entre ellos.
- Alinea el borde del objeto con la primera línea de centímetros que trae la regla, que generalmente comienza en cero.
- Toma en cuenta que el borde físico de la regla muy pocas veces coincide con el comienzo de los centímetros. Debes mantener la regla lo más plana posible y pegada al borde del objeto que quieres medir.
- Observa el otro borde del objeto e identifica el número más cercano a ese borde. Ese número te ayudará a determinar la longitud del objeto, toma en cuenta que:
- Si el borde coincide con una línea de centímetros, que son las más largas e indican un número, el objeto tiene esa cantidad de centímetros de largo. Veamos como ejemplo la medición del largo de una libreta.

En este ejemplo la libreta mide 11 cm de largo.
- Si el borde no coincide con un número entero, debes observar los números entre los que se encuentra el borde y seleccionar el menor. Ese es el número entero de centímetros.
- Luego debes agregar a este número la cantidad de rayitas más pequeñas que corresponden con los milímetros.
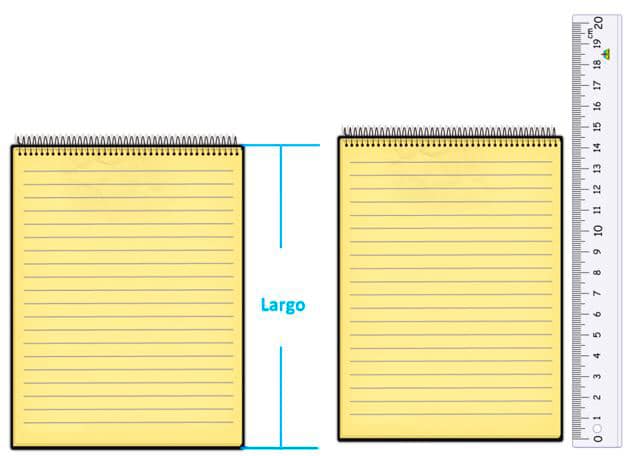
- En nuestro ejemplo el borde queda entre los números 14 y 15. Por lo que tomamos el número entero 14.
- Luego, al contar las rayitas más pequeñas vemos que hay 5.
- Por ello, decimos que la libreta mide 14 centímetros y 5 milímetros de ancho.
¿Qué es el metro?
La manera en la que se han determinado las unidades de longitud ha variado a través de los siglos. Hace muchísimo tiempo, la base de referencia para las medidas de longitud era el cuerpo humano, es decir, la longitud aproximada de cierto objeto se podía determinar con la ayuda de la mano, el codo, el brazo, entre otras partes de nuestro cuerpo. Por esa razón te presentamos algunas de las formas en las que podemos medir un metro con la ayuda del cuerpo humano.
El metro y las medidas antropométricas
El codo es una unidad que indica la longitud desde el codo hasta la punta de los dedos. Esta unidad fue utilizada en culturas antiguas como Mesopotamia, Egipto y Roma. La longitud desde el codo hasta la punta de los dedos de una persona adulta es entre 45 y 50 centímetros.

Dos veces un codo mide aproximadamente 100 centímetros lo que equivale a un 1 metro. Entonces, una persona adulta puede utilizar el codo y compararlo con el objeto que desee medir y obtener de esta manera una medida aproximada.
Con nuestras manos también podemos medir un metro, por ejemplo la anchura de la palma de la mano, en una persona adulta, es de aproximadamente 10 centímetros. Entonces, 10 veces la anchura de la palma de la mano es equivalente a 100 centímetros que es igual a 1 metro.

Otra manera de medir un metro con nuestro cuerpo es estirando uno de nuestros brazos y midiendo desde el hombro del brazo que no está estirado hasta el final de la mano abierta del brazo que hemos extendido.

Tomado de: www.fao.org
La cinta métrica
La medición de longitud es un proceso de comparación entre dos objetos y la asignación de un número. Cuando deseamos establecer la longitud del largo de una pared, una mesa o una puerta, utilizamos una cinta métrica, generalmente en metros. Es decir, elegimos como unidad básica el metro y se compara el largo del objeto que deseamos medir con el largo del centímetro y así obtenemos la medida.

Definiciones formales del metro
El metro es una de las siete unidades básicas del Sistema Internacional de Unidades (las otras seis son: kilogramo, segundo, kelvin, amperio, mol y candela). Además:
Por ejemplo: 152 metros de longitud se puede escribir como 152 m.
- Otras definiciones serían:
- Para los científicos un metro es la distancia que recorre la luz en el vacío durante un intervalo de 1/299.792.458 de segundo.
- En un principio el metro fue definido por la Academia Francesa de las Ciencias (1971) como la diezmillonésima parte de la distancia que separa el polo norte de la línea del ecuador terrestre, a través de la superficie terrestre.

Múltiplos y submúltiplos del metro
Algunos de los múltiplos más utilizados son el decámetro, el hectómetro y el kilómetro. La relación de equivalencia que se establece entre estos múltiplos y el metro es:
- 1 decámetro equivale a 10 metros.
- 1 hectómetro es igual a 100 metros.
- 1 kilómetro equivale a 1000 metros.
Múltiplos del metro | ||
| Valor | Símbolo | Nombre |
| 101 m = 10 m | dam | Decámetro |
| 102 m = 100 m | hm | Hectómetro |
| 103 m = 1.000 m | km | Kilómetro |
| 104 m = 10.000 m | mam | Miriámetro |
Los submúltiplos más utilizados en la vida cotidiana son el milímetro, el centímetro y el decímetro. La relación de equivalencia que se establece entre estos submúltiplos y el metro es:
- 1 milímetro equivale a 0,001 metros
- 1 centímetro equivale a 0.01 metros
- 1 decímetro equivale a 0,1 metros
Submúltiplos del metro | ||
| Valor | Símbolo | Nombre |
| 10-1 m = 0,1 m | dm | Decímetro |
| 10-2 m = 0,001 m | cm | Centímetro |
| 10-3 m = 0,001 m | mm | Milímetro |
Utiliza la siguiente ficha para aclarar o recordar mejor las cosas leídas hasta este punto sobre la longitud.
Tabla de conversión de unidades de longitud
En esta sección te explicaremos cómo funciona la tabla de equivalencias para realizar conversiones entre las unidades de longitud.
Lo primero que debemos recordar es que el metro es una unidad básica del Sistema Métrico Decimal. Además, en este sistema los múltiplos y submúltiplos del metro varían siguiendo una escala decimal. Es decir, una unidad mayor es equivalente a diez veces la unidad inmediatamente anterior. Aquí tienes un esquema donde puedes ver fácilmente esto:
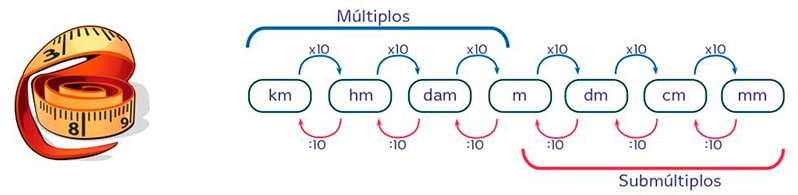
El Sistema de Numeración Decimal como su nombre indica es posicional y base diez, es decir, que diez unidades de cualquier orden equivalen a una unidad del orden inmediatamente superior. Por ejemplo:
- 10 unidades forman una decena. Veamos esto gráficamente:
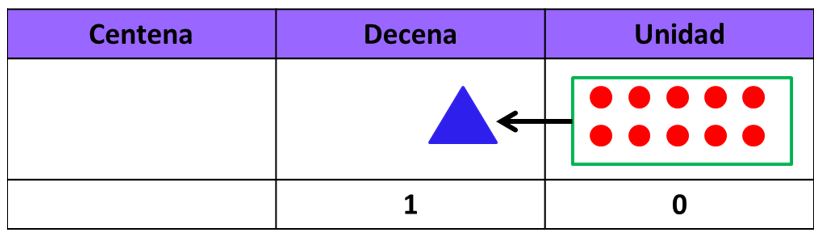
En el gráfico se observa que las 10 unidades forman una decena. Esto es así porque la base del Sistema de Numeración es diez, lo que implica que cada diez elementos representa una unidad del orden inmediatamente superior.
- 25 decenas forman dos centenas y medias o 250 unidades:
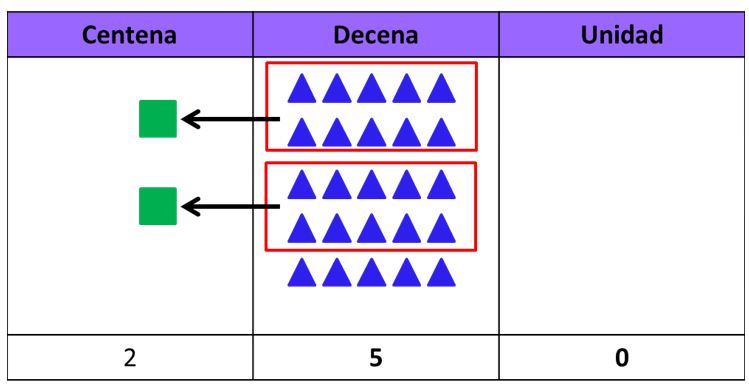
En este ejemplo tenemos 25 decenas, con las que podemos formar dos grupos de diez decenas cada uno. Cada una de estas agrupaciones equivale a una centena, por lo que nos quedan, 2 centenas y 5 decenas, lo que equivale a 250 unidades o 2 centenas y medias.
El Sistema Métrico Decimal funciona de forma similar al Sistema de Numeración Decimal, es por ello que 5 metros equivalen a: 50 decímetros, 500 centímetros, 5.000 milímetros.
Veamos esto en la tabla de equivalencias:
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 5 | ||||||
| 5 | 0 | |||||
| 5 | 0 | 0 | ||||
| 5 | 0 | 0 | 0 |
De esta manera 5 metros equivalen a:
| 5 m | |||
| 5.000 mm | 500 cm | 50 dm | 5 m |
Si ahora queremos saber a cuántos decímetros equivalen 2,3 hectómetros, representamos este valor en la tabla de equivalencias.
Para ello, es importante tener en cuenta que 2,3 hm = 2 hm + 0,3 hm. Es decir, colocaremos un 2 en la casilla de los hectómetros y un 3 en la casilla de los decámetros (0,3 hectómetros equivalen a 3 decámetros. Conviene recordar que 0,3 hectómetros se puede entender como 3 de los 10 decámetros que necesitamos para formar un hectómetro).
| km | hm | dam | m | dm | cm | mm |
| 2 | 3 | 0 | 0 |
2,3 hm equivalen a 2.300 decímetros (dm)
Apoyándonos en la tabla de equivalencias podemos realizar otras conversiones que tengan como referencia los 2,3 hm. Veamos:
| km | hm | dam | m | dm | cm | mm |
| 0 | 0 | 2 | 3 | 0 | 0 | 0 |
Teniendo en cuenta los principios que rigen el Sistema de Numeración Decimal se obtienen las siguientes equivalencias:
| 2,3 hm | ||||||
| 0,23 km | 2,3 hm | 23 dam | 230 m | 2.300 dm | 23.000 cm | 230.000 mm |
Veamos un último ejemplo. ¿1,5 km a cuántos metros equivalen?
Aplicando los principios del Sistema de Numeración Decimal y representando 12,5 km en la tabla de equivalencias, obtenemos lo siguiente:
| km | hm | dam | m | dm | cm | mm |
| 1 | 5 | 0 | 0 |
Entonces 12,5 km equivalen a 1.500 m.
Hemos visto cómo realizar conversiones entre las unidades de longitud, utilizando los principios del Sistema de Numeración Decimal y la tabla de equivalencias.
10 ejemplos de conversión de unidades de longitud
En este apartado te enseñamos ejemplos de conversión de unidades de longitud paso a paso haciendo 10 ejercicios.
- Ejercicio 1
- Vamos a pasar 25 m a hm.
- Lo primero que haremos es escribir los 25 metros en la tabla.
- Recordemos que 25 metros son 20 m + 5 m = 2 hm + 5 m
- Luego, ubicamos la unidad a la que queremos transformarla que serían hectómetros (hm).
- Lo primero que haremos es escribir los 25 metros en la tabla.
- Vamos a pasar 25 m a hm.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 0 | 0 | 2 | 5 |
Completamos con ceros hasta la unidad que le sigue y agregamos la coma para completar el número. Nos queda que:
25 m es igual a 0,025 km
- Ejercicio 2
- Ahora transformamos 0,56 m a mm.
- Empezamos escribiendo en la tabla cero metros coma cincuenta y seis.
- Después ubicamos la unidad a la que queremos transformarlos que es a mm (milímetros).
- Completamos con ceros y leemos el número resultante hasta milímetros. Tenemos que:
- Ahora transformamos 0,56 m a mm.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 0 | 5 | 6 | 0 |
0,56 m es equivalente a 560 mm
- Ejercicio 3
- Transformar 37,5 m a km.
- Comenzamos escribiendo en la tabla el número que queremos transformar, que es 37,5 m.
- Luego, localizamos los kilómetros (km) que es la unidad de medida a la que queremos llevar la cantidad.
- Ahora completamos con ceros y agregamos una coma para leer el número correctamente, y nos queda que:
- Transformar 37,5 m a km.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 0 | 0 | 3 | 7 | 5 |
37,5 m es igual a 0,00375 km
- Ejercicio 4
- Vamos a pasar 75 dam a hm.
- Lo primero que hacemos es escribir el número de decámetros que nos dan en la tabla (75 dam).
- Ubicamos la unidad a la que queremos transformarlos, que en este caso son hectómetros (hm)
- En este caso no es necesario completar con ceros para leer el número de hectómetros resultante. Nos queda:
- Vamos a pasar 75 dam a hm.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 7 | 5 |
75 dam equivalen a 7,5 hm
- Ejercicio 5
- Transformaremos 3690 mm a dm.
- empezamos escribiendo la cantidad que queremos convertir en la tabla (3690 mm).
- Luego localizamos la unidad a la que queremos transformarlos, que sería a decímetros (dm).
- En este caso no es necesario agregar ceros. Colocamos una coma en el número para leerlo correctamente, dando como resultado que:
- Transformaremos 3690 mm a dm.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 3 | 6 | 9 | 0 |
3690 mm equivale a 36,9 dm
- Ejercicio 6
- Comprobemos si la igualdad 4,69 km = 4690 m es correcta
- Primero representamos ambas cantidades en la tabla de equivalencias.
- Al completar con ceros la medida en kilómetros para llegar a metros nos damos cuenta de que son equivalentes. Por lo tanto, la igualdad es cierta.
- Comprobemos si la igualdad 4,69 km = 4690 m es correcta
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 4 | 6 | 9 | 0 |
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 4 | 6 | 9 | 0 |
- Ejercicio 7
- Verificaremos ahora esta igualdad 780 cm = 0,78 m.
- Escribimos ambas cantidades en la tabla de equivalencias.
- En este caso vemos que las cantidades no coinciden al escribirlas en la tabla. En conclusión, la igualdad es falsa.
- Verificaremos ahora esta igualdad 780 cm = 0,78 m.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 7 | 8 | 0 |
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 0 | 7 | 8 |
- Ejercicio 8
- Veamos si la igualdad 3650 mm = 0,365 dam es cierta.
- Emplearemos la tabla de equivalencias.
- Como puedes observar, al completar la cantidad de decámetros con cero hasta llegar a los milímetros, las cantidades en milímetros (mm) y decámetros (dam) son equivalentes. Esto implica que la igualdad es cierta.
- Veamos si la igualdad 3650 mm = 0,365 dam es cierta.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 3 | 6 | 5 | 0 |
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 0 | 3 | 6 | 5 | 0 |
- Ejercicio 9
- Comprobemos si 0,6 m = 600 dm es una igualdad cierta o falsa.
- Escribimos entonces ambas cantidades en la tabla de equivalencias.
- Observamos que las cantidades no coinciden, por lo que la igualdad 0,6 m = 600 dm es falsa.
- Comprobemos si 0,6 m = 600 dm es una igualdad cierta o falsa.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 0 | 6 |
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 6 | 0 | 0 |
- Ejercicio 10
- Verifiquemos la veracidad de la igualdad 4 m = 0,004 km usando la tabla de equivalencias.
- Escribimos ambas cantidades en la tabla para compararlas.
- Al completar con ceros la cantidad en metros para llegar hasta los kilómetros vemos que ambas cantidades son equivalentes, por lo que la igualdad es cierta.
- Verifiquemos la veracidad de la igualdad 4 m = 0,004 km usando la tabla de equivalencias.
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 0 | 0 | 0 | 4 |
| Kilómetro (km) | Hectómetro (hm) | Decámetro (dam) | Metros (m) | Decímetro (dm) | Centímetro (cm) | Milímetro (mm) |
| 0 | 0 | 0 | 4 |
Seguro que estas fichas te resultan de gran utilidad.
Problemas de conversión de unidades de longitud
A continuación resolveremos cuatro problemas en los que será necesario realizar conversiones entre las unidades de longitud.
- Problema 1
- María es una niña muy hermosa. Al nacer midió 53 centímetros de longitud. Hoy en día tiene 3 años y mide 1,1 metros. ¿Cuántos centímetros ha crecido María?
- En este problema nos preguntan cuántos centímetros ha crecido María en sus tres años de vida. Y nos dan como dato su estatura al nacer (53 centímetros) y la estatura actual (1,1 metros). Nosotros debemos calcular la variación de estatura experimentada por María en el transcurso de los tres años.
- Como nos preguntan la estatura en centímetros, entonces convertimos los 1,1 metros a centímetros. Para ello, utilizaremos la tabla de equivalencias. Veamos:
- María es una niña muy hermosa. Al nacer midió 53 centímetros de longitud. Hoy en día tiene 3 años y mide 1,1 metros. ¿Cuántos centímetros ha crecido María?
| km | hm | dam | m | dm | cm | mm |
| 1 | 1 | 0 |
- En la tabla se observa que 1,1 m es equivalente a 110 cm.
- Ahora que tenemos todas las medidas en centímetros sólo nos queda saber cuál ha sido la variación de la estatura de María.
- Procedemos a restar 110 cm – 53 cm = 57 cm.
- Entonces, María ha crecido 57 centímetros en sus tres años de vida.
- Problema 2
- Andrés da 3 vueltas cada día a una pista de atletismo que mide 4 hm. ¿Cuántos kilómetros recorre Andrés luego de 7 días de entrenamiento?
- Primero debemos saber cuántos hectómetros recorre Andrés en un día, para conocer este dato es suficiente multiplicar 3 x 4 hm = 12 hm. Andrés recorre 12 hm diariamente.
- Como nos preguntan cuántos kilómetros recorre Andrés al cabo de 7 días de entrenamiento, transformaremos a kilómetros los 12 hectómetros que recorre Andrés diariamente.
- Representamos los 12 hm en la tabla de equivalencias.
- Andrés da 3 vueltas cada día a una pista de atletismo que mide 4 hm. ¿Cuántos kilómetros recorre Andrés luego de 7 días de entrenamiento?
| km | hm | dam | m | dm | cm | mm |
| 1 | 2 |
- Los 12 hm equivalen a 1,2 km. Ahora sólo falta multiplicar 1,2 km por 7 para darle respuesta a la interrogante del problema.
- 1,2 km x 7 = 8,4 km.
- Entonces, Andrés recorre 8,4 km luego de 7 días de entrenamiento.
- Problema 3:
- José nadó 0,7 km en un triatlón en el que participó. ¿Cuántos decámetros nado? ¿A cuánto equivale lo que nadó José en decímetros?
- Para responder a las preguntas de este problema representamos 0,7 km en la tabla de equivalencias. Veamos:
- José nadó 0,7 km en un triatlón en el que participó. ¿Cuántos decámetros nado? ¿A cuánto equivale lo que nadó José en decímetros?
| km | hm | dam | m | dm | cm | mm |
| 0 | 7 | 0 | 0 | 0 |
- Los 0,7 km que nadó José equivalen a 70 dam y 7.000 dm.
- Problema 4:
- Luisa necesitaba algunos trozos de cinta que midieran exactamente 1 metro y medio, sin importar su color. Buscó en su casa y encontró las cintas que aparecen en la siguiente tabla:
| Color de la cinta | Medida | Color de la cinta | Medida |
| Cinta azul | 2 m | Cinta roja | 150 cm |
| Cinta verde | 1,5 m | Cinta negra | 1,05 m |
| Cinta naranja | 0,0015 km | Cinta fucsia | 1.500 mm |
- Para saber cuáles cintas le sirven a Luisa representaremos cada una de las medidas en una tabla de equivalencia.
| km | hm | dam | m | dm | cm | mm |
| 2 | ||||||
| 1 | 5 | |||||
| 0 | 0 | 0 | 1 | 5 | ||
| 1 | 5 | 0 | ||||
| 1 | 0 | 5 | ||||
| 1 | 5 | 0 | 0 |
- Como se puede ver en la tabla de equivalencias, las cintas que le sirven a Luisa porque miden 1 metro y medio son la verde, la naranja, la roja y la fucsia.
Te dejamos una última ficha y juegos para que sigas repasando.
Selecciona un juego 👇 👇 👇

Definiciones sobre el sistema de longitud

Múltiplos y submúltiplos del metro

Equivalencias con el metro de sus múltiplos y submúltiplos

Conversión de unidades 1

Conversión de unidades 2

Problemas con el sistema de longitud

Cuestionario

Definiciones sobre el sistema de longitud

Múltiplos y submúltiplos del metro

Equivalencias con el metro de sus múltiplos y submúltiplos

Conversión de unidades 1

Conversión de unidades 2

Problemas con el sistema de longitud

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.





