Regla de tres
La regla de tres es muy útil para resolver innumerables problemas aritméticos por eso debes aprender todo sobre cómo aplicarla. En este artículo conocerás cómo hacer una regla de tres, aprenderás acerca de la regla de tres simple, la regla de tres inversa y la regla de tres con porcentajes. Además, tienes ejemplos y problemas resueltos paso a paso.
Cómo hacer una regla de tres
La regla de tres es un procedimiento muy usado en matemática por su utilidad en problemas relacionados con magnitudes proporcionales. Esta regla se usa para determinar una cuarta cantidad relacionando otras tres que se encuentran en proporción directa o inversa.
Para saber cómo hacer una regla de tres es muy importante conocer si las magnitudes son directamente proporcionales o inversamente proporcionales porque esto nos dirá si es una regla de tres simple directa o inversa. Veamos:
Para la regla de tres simple:
Para saber cómo hacer la regla de tres directa debemos aprender esto:
Por ejemplo:
- Si un kilogramo de mango cuesta 3 euros, ¿cuánto pagaré por 2 kilogramos?
- Observa la tabla porque allí está la respuesta.
- En este caso tenemos dos magnitudes que son la cantidad de kilogramos de mangos (Kg) y el dinero en Euros (€).
| Kg | 1 | 2 | 0,5 | 3 | 4 | 5 |
| € | 3 | 6 | 1,5 | 9 | 12 | x |
- Estas dos magnitudes son directamente proporcionales por lo que para encontrar encontrar el valor de x podemos establecer una relación como esta:
31 = x5
Se lee “3 es a 1 como x es a 5”.
- Esto es fundamental para saber cómo hacer una regla de tres simple, que te explicaremos paso a paso en el siguiente apartado. En ese apartado hallaremos el valor en euros de 5 kg de mango, es decir, hallaremos el valor de x usando una regla de tres simple.
Para la regla de tres inversa:
En el caso de la regla de tres inversa debemos tener claro lo siguiente:
Por ejemplo:
- El tiempo de recolección de las cosechas es de 12 días cuando se encargan de ello 18 personas. ¿Cuánto tardarán 54 personas en recoger las cosechas?
- En la siguiente tabla se encuentra la respuesta. Observa.
- Las dos magnitudes aquí son el Número de personas y el Tiempo en días.
| Número de personas | 18 | 9 | 36 | 72 | 54 | x |
| Tiempo (días) | 12 | 24 | 6 | 3 | 4 | 2 |
- Estas dos magnitudes son inversamente proporcionales por lo que para encontrar el valor de x podemos establecer la siguiente relación:
54 . 4 = x . 2
- Reconocer este tipo de relación inversamente proporcional entre magnitudes es fundamental para saber cómo hacer una regla de tres inversa, lo cual te explicaremos detalladamente más adelante en otro apartado de este artículo.
- En esa sección también hallaremos el valor de x aplicando una regla de tres inversa, es decir, sabremos cuántas personas se requieren para solo tardar 2 días recogiendo la cosecha.
Regla de tres simple
La regla de tres simple se usa para conocer un número desconocido “x” que está relacionado en proporción directa con otro número “b”, siempre y cuando conozcamos otros dos números “a” y “c” que guardan la misma proporción de “x” y “b”.
Podemos plantear esta regla de tres:
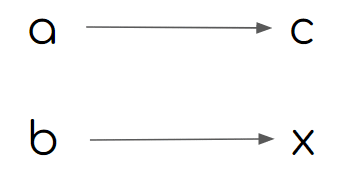
Para obtener el valor de x procedemos así:

Ejemplo de regla de tres directa
- Veamos cómo hallar el valor de x en el ejemplo sobre mangos del apartado anterior.
- En ese caso teníamos la siguiente tabla que relaciona dos magnitudes: kilogramos de mangos (Kg) y el dinero en Euros (€).
- Recordemos que por 1 kg de mango pagaría 3 euros. Observa la tabla:
| Kg | 1 | 2 | 0,5 | 3 | 4 | 5 |
| € | 3 | 6 | 1,5 | 9 | 12 | x |
- Ahora bien, en este caso vamos a tomar la columna que hemos resaltado para hacer la regla de tres que nos permitirá saber el valor de x. Es decir, el valor en euros de 5 Kg de mangos.
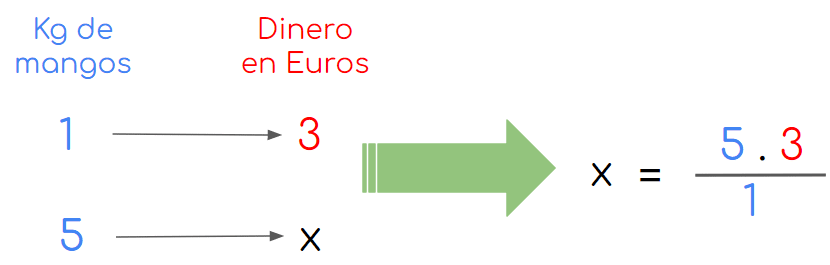
- De ahí obtenemos que:
x = 151 = 15
- Por ello, decimos que el valor de 5 kg de mangos es 15 euros.
Mira este otro ejemplo de regla de tres directa:
- Diego debe pintar completamente una habitación de 45 m2. Cuando va a comprar la pintura se encuentra con que un bote de pintura le alcanza para pintar 9 m2 de superficie. ¿Cuántos botes de pintura debe comprar Diego para poder pintar toda la habitación?
- En este caso relacionamos el número de m2 de pared con el número de botes de pintura. Si los m2 de pared aumentan también aumentan los botes de pintura que se requieren.
- Y lo mismo ocurre si el número de m2 de pared disminuye, disminuirá el número de botes necesarios para pintarla.
- Aquí vemos que la regla de tres es directa porque las magnitudes son directamente proporcionales.
- Podemos entonces plantear la regla de tres directa así:
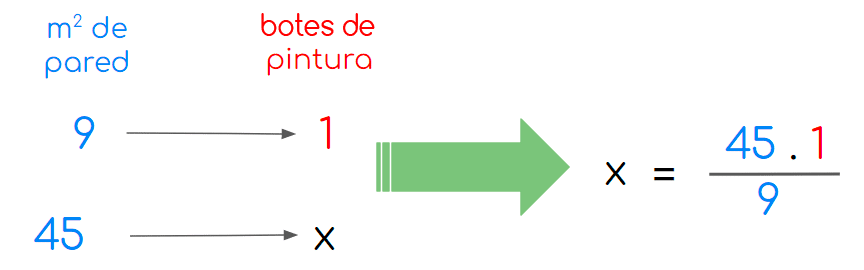
- Así que:
x = 459 = 5
- Por tanto, para pintar 45 m2 de pared Diego debe comprar 5 botes de pintura.
Regla de tres inversa
La regla de tres inversa se emplea para encontrar un número “x” que desconocemos y que es inversamente proporcional a un número “b”, apoyándonos en otro par de números “a” y “c” que están en igual proporción inversa que “x” y “b”.
Sabiendo lo anterior, podemos plantear una regla de tres:

Para hallar el valor de x, si se tratara de regla de tres directa quedaría así:
ab = cx
Pero en la regla de tres inversa vamos a invertir una de las dos fracciones, trataremos siempre que la x quede en el numerador:
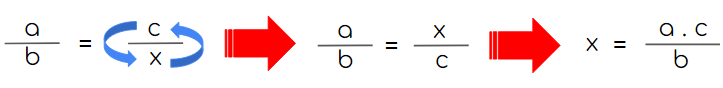
Esto podemos resumirlo así:
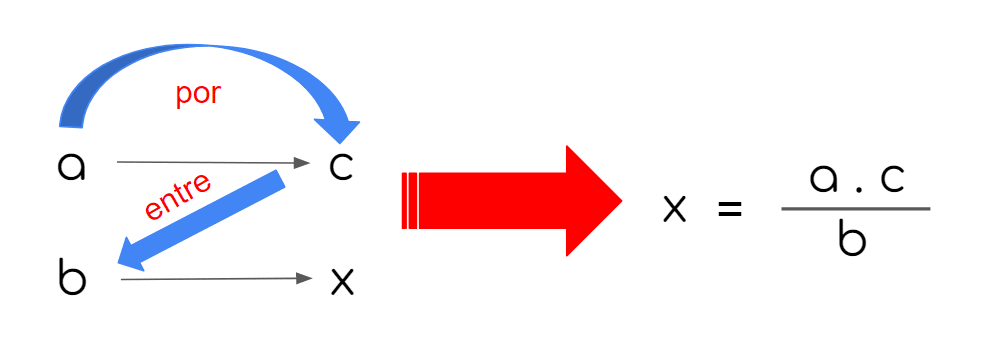
Vamos a ver un ejemplo de cómo resolver una regla de tres inversa con la situación que planteamos en el primer apartado de este artículo acerca de la recolección de las cosechas.
- Esta tabla resume la información acerca del tiempo (en días) de recolección de las cosechas con base en el número de personas trabajando en ello:
| Número de personas | 18 | 9 | 36 | 72 | 54 | x |
| Tiempo (días) | 12 | 24 | 6 | 3 | 4 | 2 |
- Como vemos, al aumentar el número de personas disminuye el tiempo de recolección de las cosechas, y al disminuir el número de personas el tiempo en días aumenta. Por ello, las magnitudes son inversamente proporcionales.
- Esto nos indica que es una regla de tres inversa.
- Para hallar el valor de x usando una regla de tres inversa planteamos lo siguiente:
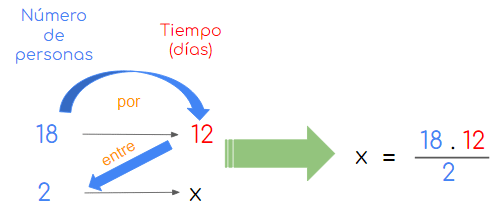
- De donde:
x = 2162 = 108
- Esto quiere decir que si 2 personas se ocupan de recolectar las cosechas tardarían 108 días, lo que sería un poco más de tres meses.
Veamos otro ejemplo de cómo resolver una regla de tres inversa:
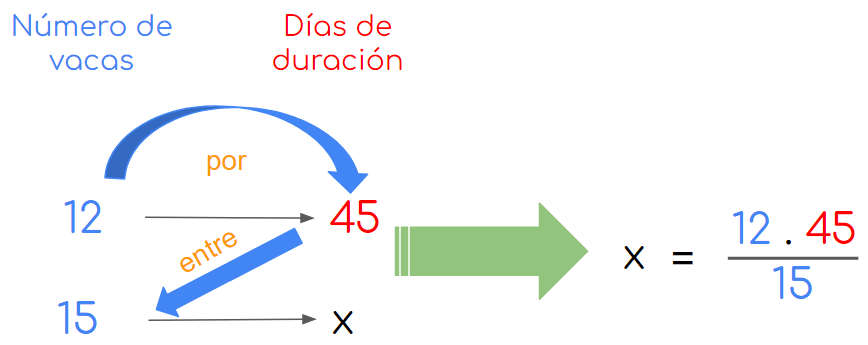
- El saco de alimento para vacas que usa Simón en su granja dura 45 días para las 12 vacas que tiene. Si piensa adquirir 3 vacas, ¿cuánto tiempo le durará el alimento?
- En este caso vemos que si aumenta el número de vacas disminuye el número de días que dura el alimento. Y si disminuye el número de vacas aumenta el número de días que dura el alimento.
- Esto nos indica que las magnitudes número de vacas y días que dura el alimento son inversamente proporcionales. Por tanto, vamos a usar regla de tres inversa para determinar el tiempo que dura el alimento.
- Lo primero que debemos considerar es que Simón ahora tendrá 15 vacas, si compra las 3 que tiene pensado.
- Ahora planteamos la regla de tres inversa correspondiente:
- Tenemos que:
x = 54015 = 36
- Esto quiere decir que si Simón compra 3 vacas más, lo que harían un total de 15 vacas, el alimento le durará 36 días.
Regla de tres con porcentajes
La regla de tres con porcentajes es un cálculo muy utilizado por todos nosotros. Por ejemplo, cuando vamos al mercado y vemos una rebaja de 10% la aplicamos para conocer el precio final del producto.
También, la podemos utilizar para saber el porcentaje de hombres y mujeres que hay en un salón o para determinar el porcentaje de soluto y solvente con el que cuenta una solución.
Debido a su importancia, te invitamos a que prestes mucha atención a cómo se utiliza la regla de tres con porcentajes. Estamos seguros que más temprano que tarde la vas a necesitar.
Lo primero que debes hacer, a la hora de aplicar la regla de tres con porcentaje, es identificar con precisión cuál es el todo o 100 por ciento dentro de la situación o problema que deseas resolver.
A continuación, veamos dos ejemplos que nos ayudarán a comprender de qué se trata esto del todo o 100 por ciento.
Ejemplo 1:
- Supongamos en una clase hay 14 niños y te interesa saber qué porcentaje del total de alumnos varones representa este número. ¿Cuál sería tu respuesta?
- Como te habrás podido dar cuenta, en este caso no es posible establecer qué porcentaje del total representan los 14 estudiantes varones. Esto debido a que en la situación no se dice cuál es el todo o 100 por ciento.
- Para resolver problemas y ejercicios donde se aplique la regla de tres con porcentajes, es importantísimo establecer cuál es el 100%.
- Veamos ahora, cómo quedaría el planteamiento que nos permite saber qué porcentaje del total representan los 14 varones.
- En una clase hay 14 niños y 21 niñas. ¿Qué porcentaje del total representan los 14 niños?
- En este caso, sí es posible establecer qué porcentaje representan los 14 estudiantes varones, porque sabemos que el total de estudiantes es igual a 35 (14 varones + 21 hembras = 35).
- Para aplicar la regla de tres con porcentajes, es fundamental que identifiques cuál es el total o 100 por ciento. Una vez cumplido con este paso podrás avanzar con mayor facilidad en la realización de este cálculo.
- Veamos cómo aplicaríamos la regla de tres con porcentajes en el problema del salón de clases.
- El total de estudiantes en el salón es 35, este número se obtiene sumando 14 + 21 que es el número de varones más el número de hembras que hay en el aula.
- Como ya sabemos cuál es el 100%, planteamos la regla de tres con porcentajes. Veamos:
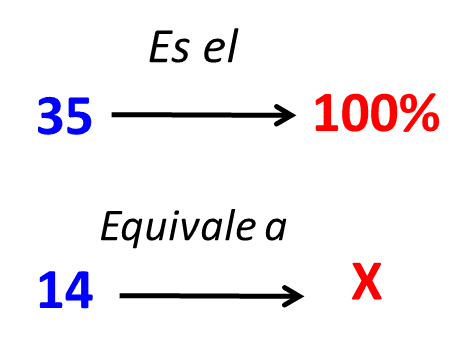
- En el planteamiento de esta regla de tres tenemos que 35 es el 100% y queremos saber a qué porcentaje equivalen los 14 estudiantes varones.
- Para conocer este dato multiplicamos 14 por 100% y el resultado lo dividimos entre 35.
x = 14 . 100%35
x = 1400%35
x= 40%
- El 40% de los estudiantes del salón son niños.
- Si queremos saber el porcentaje de niñas en el salón restamos 100% – 40% = 60%.
- Es decir, el 60% de los estudiantes son niñas.
Analizaremos otra situación en la que también se aplica la regla de tres con porcentajes.
- La población extranjera residente en España para enero de 2021 ascendía a 5.375.971 personas. De ellas, 14% aproximadamente eran de origen marroquí y el 12% era de Rumanía. Para saber el número de personas procedentes de Marruecos y Rumanía que residen en España, podemos aplicar la regla de tres con porcentajes.
- Como ya hemos dicho es importante que primero establezcamos cuál es el 100%.
- En este caso el 100 por ciento es equivalente a las 5.375.971 personas extranjeras que residen en España.
- Conociendo este dato pasemos a plantear nuestras reglas de tres con porcentajes.
- En esta regla de tres tenemos que 5.375.971 equivale al 100% y queremos saber cuánto es el 14% del total.
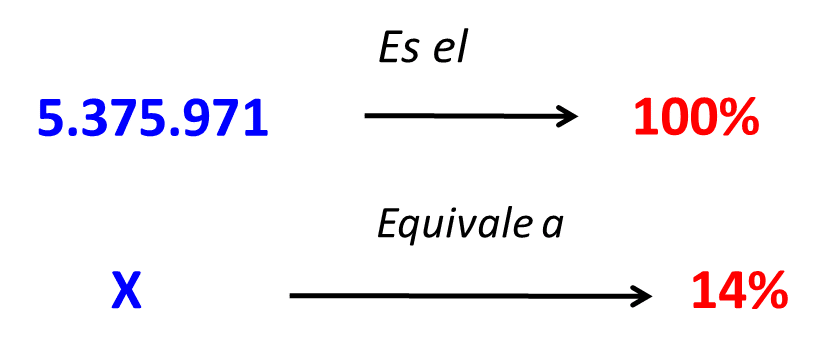
- Para determinar el valor de X multiplicamos 14% por 5.375.971 y luego lo dividimos entre 100%.
x = 14% . 5.375.971100%
x = 75.263.594100
x= 72.635,94 ≈ 752.636
- Con la resolución de esta regla de tres con porcentajes, obtenemos que 752.636 de los extranjeros residentes en España son de Marruecos.
- Ahora veamos cuántos extranjeros residentes en España son de Rumanía. Para ello planteamos una nueva regla de tres.
- Tenemos que 5.375.971 equivale al 100% y deseamos conocer cuál es el 12% del total.
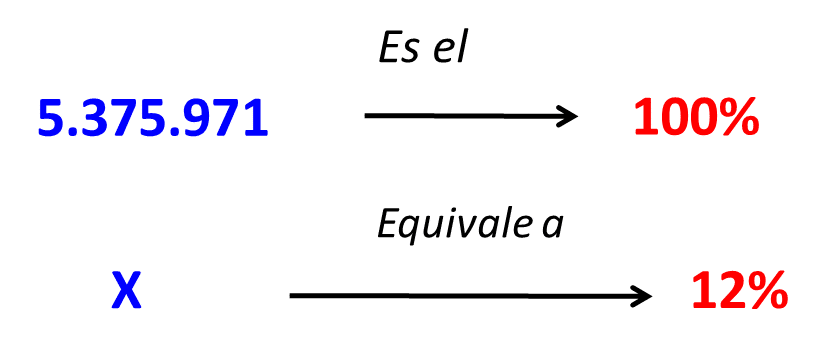
- Calculamos el valor de X multiplicando 12% por 5.375.971 y luego lo dividimos en 100%.
x = 12% . 5.375.971100%
x = 64.511.652100
x= 645.116,52 ≈ 645.117
- Los extranjeros que residen en España y provienen de Rumanía son 645.117.
- Al sumar 752.636 con 645.117 obtenemos como suma 1.397.753. Este resultado es el número de personas extranjeras residentes en España que provienen de Marruecos y Rumanía…
Hemos visto en este apartado la gran utilidad que tiene la regla de tres con porcentajes.
Ejemplos de regla de tres
Para que no te quedes con dudas, en esta sección estudiaremos dos ejemplos en los que se aplica la regla de tres.
Ejemplo 1:
- Julia prepara una rica mermelada de fresas. Lo primero que hace es lavar bien la fruta, luego le coloca tres cuartos de kg de azúcar por cada kilogramo de fresa. Por último, deja cocer las fresas hasta que tenga una consistencia bastante espesa. Si Julia quiere preparar mermelada con 2 kg de fresa, ¿cuánto azúcar necesita?
- Como no todas las personas hacen la misma cantidad de mermelada, vamos a construir una tabla en la que registraremos la cantidad de azúcar necesaria, para diferentes cantidades de mermelada de fresas. Veamos:
- Esta tabla la hemos completado aplicando una regla de tres directa.
| Fresas (kg) | 1 | 2 | 3 | 4 |
| Azúcar (kg) | 34 | 64 = 32 | 34 | 124 = 3 |
- Sabemos que para 1 kilogramo de fruta necesitamos 3/4 kg de azúcar. La pregunta que debemos responder es, cuánta azúcar necesitamos para 2 kg de fruta. Para dar respuesta a esta pregunta planteamos una regla de tres directa.
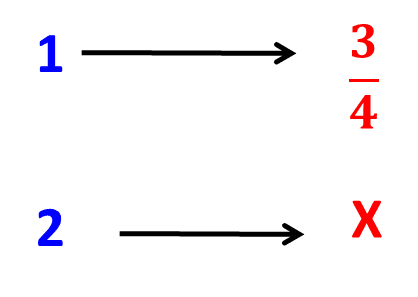
- Luego de planteada la regla de tres nos toca llevar a cabo su resolución:
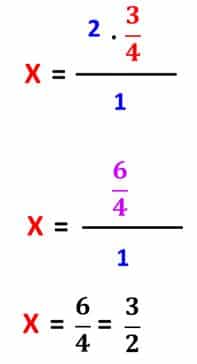
- Al resolver obtenemos que para 2 kg de fruta necesitamos kg de azúcar.
- De la misma manera se pueden calcular los otros valores de la tabla.
Ejemplo 2:
- Consideremos un rectángulo de 24 cm de base y 1 cm de altura. Vamos a buscar una familia de rectángulos que tengan la misma área.
- Comenzamos calculando el área del rectángulo dado, cuya base es 24 cm y su altura es 1 cm.

- El área de este rectángulo se calcula de la siguiente manera:
- A = b . h
- A = 24 cm . 1 cm
- A = 24 cm²
- El área del rectángulo de base 24 cm y altura 1 cm es 24 cm2
- El área de este rectángulo se calcula de la siguiente manera:
- Ahora vamos a buscar otros rectángulos que tengan la misma área. Veamos:
 | 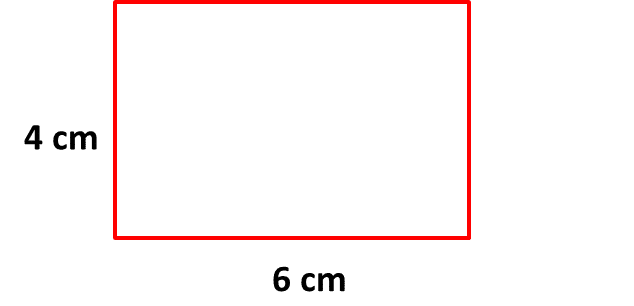 |  |
| A = b . h | A = b . h | A = b . h |
| A = 12 cm . 2 cm | A = 6 cm . 4 cm | A = 8 cm . 3 cm |
| A = 24 cm² | A = 24 cm² | A = 24 cm² |
- Hemos encontrado 4 rectángulos distintos cuya área es 24 cm2.
- Organicemos toda esta información en una tabla, para establecer cuál es el comportamiento de estas magnitudes. Veamos:
| Base en cm | Altura en cm |
| 24 | 1 |
| 12 | 2 |
| 6 | 4 |
| 3 | x |
- En la tabla se observa que, si la base del rectángulo se reduce a la mitad, entonces la altura se duplica. Esto es:
- Cuando la altura se duplica la base se reduce a la mitad.
- Esto quiere decir que las magnitudes (Base y Altura) mantienen un comportamiento inversamente proporcional.
- Si queremos conocer el valor de x para completar la tabla establecemos una regla de tres inversa como ésta (usaremos las filas resaltadas en la tabla):
- En la tabla se observa que, si la base del rectángulo se reduce a la mitad, entonces la altura se duplica. Esto es:
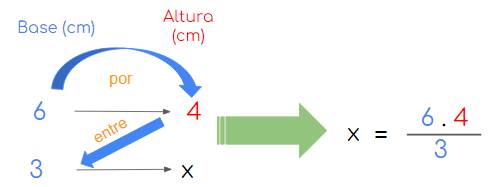
- Tenemos entonces que:
x = 243 = 8
- Esto quiere decir que un rectángulo de 24 cm2 de área, cuya base mide 3 cm, tiene una altura de 8 cm.
Problemas de regla de tres
En este apartado resolveremos problemas que te ayudarán a consolidar el cálculo de la regla de tres y a desarrollar tu pensamiento matemático.
Problema 1
- En un país este año hubo 73 días de lluvias. ¿Qué porcentaje del año significa esto?
- Lo primero que debemos hacer es identificar cuál es el 100 por ciento.
- Para lograrlo debemos tener en cuenta que en el problema nos dicen que en un país hubo 73 días de lluvia y nos preguntan qué porcentaje significa esto del año.
- La clave aquí es identificar que 1 año que equivale a 365 días que es el todo o 100%.
- Habiendo deducido este dato, pasamos ahora a plantear la regla de tres. Veamos:
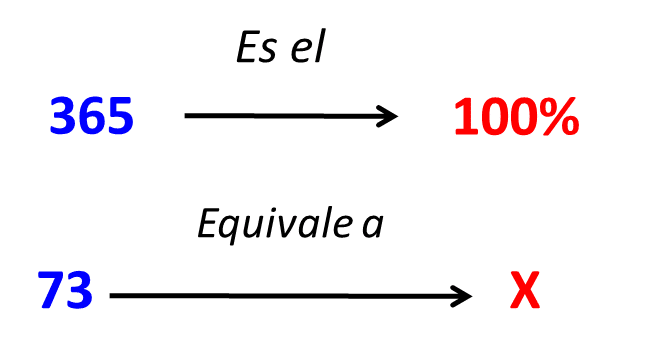
- Para resolver esta regla de tres multiplicamos 73 por 100% y el resultado lo dividimos entre 365. No olvidemos que nuestra respuesta debe estar expresada en términos de porcentajes.
x = 73 . 100%365
x = 7.300%365
x= 20%
- Concluimos, que en ese país durante el 20% del año hubo lluvias.
Problema 2:
- Una compañía cuenta con un camión con capacidad de 3.000 kg. Este camión debe dar 15 viajes para transportar la mercancía que llega semanalmente al puerto. Si van a contratar ahora un camión con capacidad de carga de 4.500 kg, ¿cuántos viajes debe dar este camión para transportar la misma carga?
- Las magnitudes son el número de kilogramos de carga del camión y el número de viajes que debe dar.
- Si la capacidad de carga del camión aumenta, el número de viajes disminuye, por lo tanto, las magnitudes son inversamente proporcionales y usamos una regla de tres inversa.
- Vamos a plantear la regla de tres correspondiente:

- Por tanto:
x = 45.0004.500 = 10
- Podemos decir entonces que el nuevo camión debe dar 10 viajes para transportar la mercancía.
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇

Definición de regla de tres

Tipos de regla de tres

Cálculo de la regla de tres - 1

Cálculo de la regla de tres - 2

Cálculo de la regla de tres - 3

Regla de tres con porcentajes

Definición de regla de tres

Tipos de regla de tres
Cálculo de la regla de tres - 1
Cálculo de la regla de tres - 2

Cálculo de la regla de tres - 3

Regla de tres con porcentajes
![]() Registrado en SafeCreative.
Registrado en SafeCreative.