Raíz cuadrada
Tal vez has visto en libros o páginas web el símbolo de la raíz cuadrada. Su símbolo llama la atención y muchos desean saber para qué sirve, cómo se utiliza y por qué tiene esta forma:

En este artículo te vamos a explicar de forma detallada y sencilla qué es una raíz cuadrada, cuáles son sus partes, para qué sirve, cómo se calcula, además te mostraremos algunos ejercicios en los que se aplica la idea de raíz cuadrada.
Estamos seguros que si lees todo el artículo con mucha atención, te quedará clara la idea de raíz cuadrada, lo que te ayudará resolver ejercicios y problemas en los que debas aplicar este concepto matemático.
Qué es la raíz cuadrada de un número
Por ejemplo:
- 8 es raíz cuadrada de 64, porque 8 x 8 = 64
- 10 es raíz cuadrada de 100, ya que 10 x 10 = 100
- 13 es raíz cuadrada de 169, debido a que 13 x 13 = 169
Si ya has estudiado los números enteros, entonces estás listo para visualizar que:
- – 8 también es raíz cuadrada de 64, porque ( – 8) x ( – 8) = 64
- – 10 también es raíz cuadrada de 100, ya que ( – 10) x ( – 10) = 100
- – 13 también es raíz cuadrada de 169, porque ( – 13) x ( – 13) = 169
El símbolo de la raíz cuadrada es:

Y se lee, raíz cuadrada de… Por ejemplo:
| Se lee raíz cuadrada de 144. | |
| Se lee raíz cuadrada de 81. | |
| Se lee raíz cuadrada de 324 |
Partes de la raíz cuadrada
A la hora de calcular o de resolver un problema que involucre la raíz cuadrada es muy importante conocer las partes que forman este símbolo matemático. Esto te facilitará la comprensión del planteamiento matemático que tienes enfrente.
Presta mucha atención, porque aquí te decimos cuáles son las partes de una raíz cuadrada.
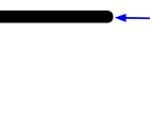 | Radical: Es el símbolo que indica que la operación es una raíz. Como dato curioso te contamos que el signo de la raíz es una variante de la letra r en latín. |
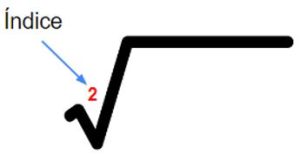 | Índice: Indica el grado de la raíz. Es el número al que debe elevarse la raíz para obtener la cantidad subradical. Cuando no tiene un número como índice, decimos que se trata de una raíz cuadrada. |
 | Cantidad subradical o radicando: Es el número al que se le calcula la raíz. Aparece escrito debajo del signo radical. |
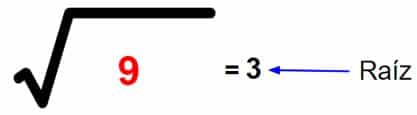 | Raíz: Es un número que al ser empleado dos veces como factor en una multiplicación da como resultado la cantidad subradical. |
Para qué sirve la raíz cuadrada
En este apartado veremos algunos ejemplos en los que se utiliza la raíz cuadrada.
Cuadrado de lado igual a 1
La raíz cuadrada surge a partir de un problema geométrico, que consiste en calcular la longitud de la diagonal de un cuadrado.
Existe un caso muy famoso en la historia de la matemática que se basa en calcular la longitud de la diagonal de un cuadrado de lado igual a 1.
La resolución de este problema se le atribuye a Pitágoras.
- En este problema la longitud de la diagonal es:
- Se obtiene al aplicar el Teorema de Pitágoras.
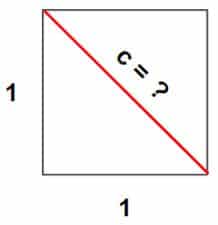
- En este caso Pitágoras aplicó el teorema que lleva su nombre y obtuvo lo siguiente:
- Recuerda que el Teorema de Pitágoras afirma que:

El Papiro de Rhind

Resolución de ecuaciones
Por ejemplo, si queremos hallar un número que elevado al cuadrado dé como resultado 144 aplicamos la definición de raíz cuadrada.
Veamos:
- Al número que queremos hallar los llamaremos X.
- El enunciado nos dice que X elevado al cuadrado es igual a 144. Esto es:
- Ahora debemos hallar el o los números que elevados al cuadrado den como resultado 144. Aplicando la definición de raíz cuadrada tenemos que esos números son 12 y -12.
- Concluimos que:
Ejemplos de raíz cuadrada
Cómo vimos anteriormente, la raíz cuadrada de un número es otro número que al ser multiplicado por sí mismo nos da como resultado el número inicial.
Algunos ejemplos notables de raíz cuadrada que debes manejar muy bien son los siguientes:

- Algo que debes tener en cuenta, si ya conoces los números enteros, es que:
- Es decir:
- Esto significa que la raíz cuadrada de 4 también es -2.
- Podemos escribir entonces que:
- Esto lo podemos resumir así:
- Lo mismo ocurre con todas las raíces cuadradas que dimos como ejemplo:
- Fíjate que todos los números a los que les calculamos la raíz cuadrada eran números enteros positivos.
- Podemos concluir que:
Ejemplos geométricos de raíz cuadrada
Observa este cuadrado que tiene 16 cuadritos:
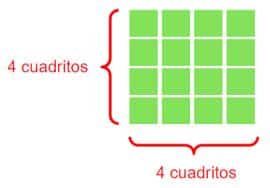
En este caso podemos visualizar la raíz de 16 como uno de los lados del cuadrado que mide 4 cuadritos. Recordemos que (4 al cuadrado es igual a 16).
Mira este cuadrado que tiene 100 cuadritos:
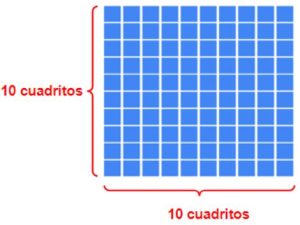
Como ves, cada lado tiene 10 cuadraditos por lo que se puede visualizar fácilmente que 10 es la raíz cuadrada de 100. Pues (10 al cuadrado es igual a 100).
Presta atención a este tablero de damas. Es cuadrado y está formado por 64 cuadritos en total, 32 blancos y 32 negros:

Cada lado tiene 8 cuadritos. Aquí podemos visualizar que la raíz cuadrada de 64 es 8, ya que (8 al cuadrado es igual a 64).
Cómo sacar la raíz cuadrada
En este apartado te enseñaremos cómo calcular una raíz cuadrada paso a paso (sin calculadora).
Calcularemos la raíz cuadrada de 98765.
- Primero vamos a escribir lo siguiente:
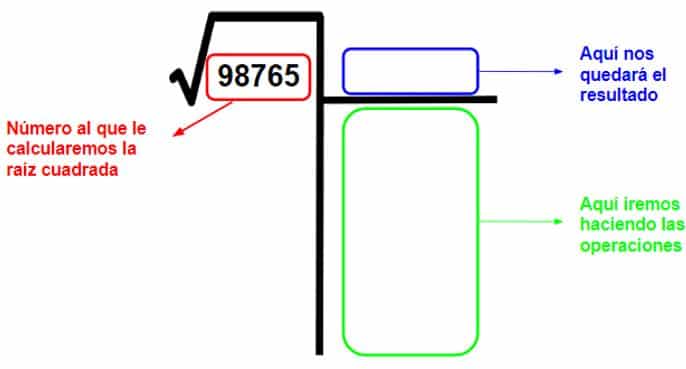
- Ahora separamos las cifras del número al que vamos a calcularle la raíz cuadrada de dos cifras en dos cifras, comenzando de izquierda a derecha:
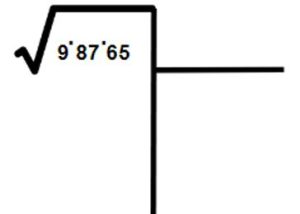
- Empezamos a trabajar con los grupos de números de izquierda a derecha. En este caso, el primero es el número 9.
- Vamos a buscar un número que multiplicado por sí mismo nos de 9, o lo más cerca posible de 9, sin pasarse. En este caso sería 3 porque 3² = 9. Nos queda así:
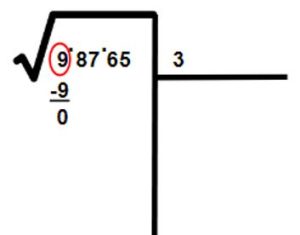
- Lo que hicimos fue colocar el 3 en el lugar de los resultados y el 9, que es producto obtenido al multiplicar 3 por sí mismo, en el lugar de las operaciones.
- Después restamos de la misma forma que lo hacemos cuando estamos realizando una división.
- Ahora vamos a trabajar con el segundo grupo de números, que en este caso es 87.
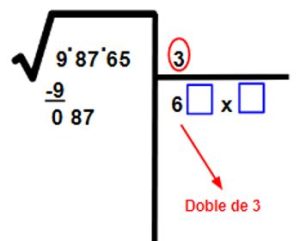
- Lo que hicimos fue bajar el siguiente par de números, que en este caso es 87. Y escribimos en el área de operaciones el doble del número que está en el área de resultados, es decir 6.
- Ahora vamos a colocar en los cuadrados azules el mismo número, de tal forma que el resultado de la operación indicada sea 87, o un número que se aproxime sin pasarse. Por ejemplo:

- Escogemos el 1 y lo escribimos al lado del 3 en el área de resultados. Luego, restamos con el 87. Nos queda así:
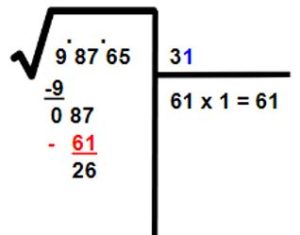
- Ahora bajamos el último grupo de dos números, que en este caso es 65. Y escribimos en el área de las operaciones el doble de los números que están en el área de los resultados.
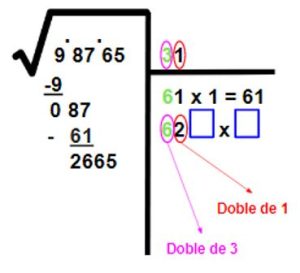
- Luego, buscamos un número para colocar en los cuadritos para que el resultado de la operación sea 2665, o un número cercano que no se pase:

- Escogemos el 4 y lo escribimos al lado del 1 en el área de resultados. Luego, restamos 2496.
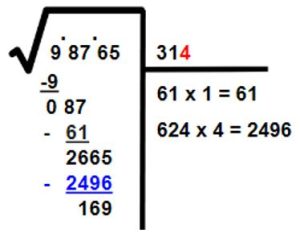
- Podemos decir que:
- Esto se lee la raíz cuadrada de 98765 es aproximadamente 314.
- Hemos concluido el cálculo de la raíz cuadrada (sin sacar decimales).
- Para comprobar que hemos llegado al resultado correcto hacemos lo siguiente:
- Ahora sumamos el resultado de la última resta, y tenemos:
- Como ves, 98765 es el número al que estamos calculándole la raíz cuadrada.
Para seguir sacando la raíz con decimales, realizamos el siguiente procedimiento:
- Agregamos dos ceros al resultado de la última resta y repetimos el proceso. Nos quedaría así:
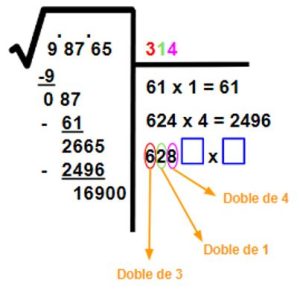
- Buscamos un número tal que, al colocarlo en los cuadros azules, el resultado de la operación sea 16.900, o el número más cercano que no se pase. Veamos:

- Escogemos el 2 y lo escribiremos al lado del 4 en el área de los resultados. Pero antes debemos escribir una coma porque estamos sacando decimales a la raiz cuadrada. Luego, restamos 12564.

- Por último:
Ejercicios de raíces cuadradas
En esta sección vamos a resolver ejercicios que involucren la definición y el cálculo de la raíz cuadrada.
- Calcula la raíz cuadrada de 289.
Veamos cómo se hace este cálculo:
- Paso 1: Separamos las cifras en grupos de dos, comenzando por la derecha.
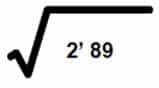
- Paso 2: Calculamos por defecto el número que elevado al cuadrado se acerque más a la cifra que ha quedado a la derecha, que en este caso es el número 2.
- El número que estamos buscando es el 1 (el 1 es el número que elevado al cuadrado queda más cerca de 2 por defecto).
- Paso 3: El número 1 (el que obtuvimos en el paso 2) lo colocamos en la casilla de la derecha. El 1 será la primera cifra de la raíz.
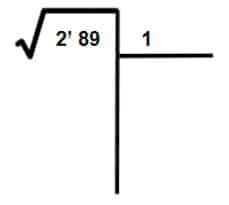
- Paso 4: El cuadrado del número 1 (12 = 1) se resta de la primera cifra de la derecha.
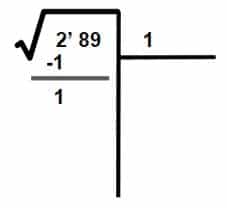
- Paso 5: A la derecha del resto que acabamos de obtener bajamos el siguiente grupo de números de la cantidad subradical (89).
- Separamos, del número que acabamos de formar, la primera cifra de la derecha (9) y dividimos el número de la izquierda (18) entre el doble del número que está en la casilla, en este caso 2 x 1 = 2.
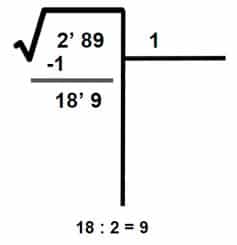
- Paso 6: Debajo de la primera casilla dibujamos otra en la que colocamos el doble que obtuvimos en el paso 5 (2 x 1 = 2), seguido del cociente de la división (9) y el número formado se multiplica por el cociente obtenido (9).
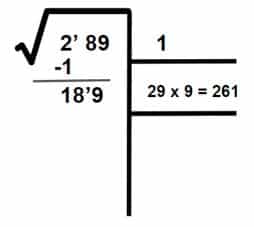
- Al ser 261 mayor que el resto (189), debemos ir probando con números menores a 9 hasta que el producto obtenido sea menor o igual que el resto.
- Veamos:
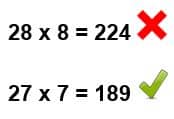
- Como el resultado de multiplicar 27 x 7 = 189 es igual al resto, entonces colocamos el 7 como segunda cifra de la raíz.
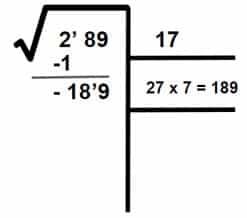
- Restamos este último producto (189) con el resto (189).
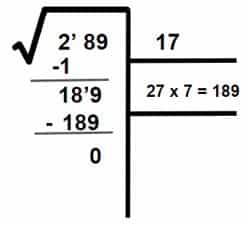
- Como el resto es igual a cero, concluimos que 17 es la raíz cuadrada de 289.
- Observa el siguiente cuadrado que tiene 15 lados de cuadrito de lado:
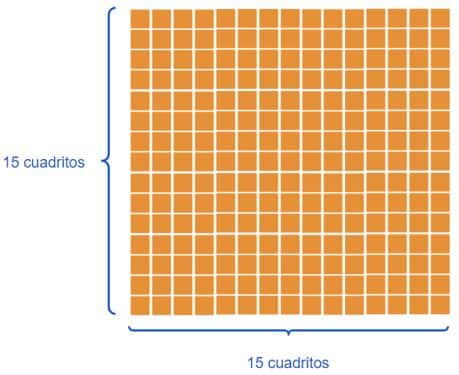
- Responde: ¿De cuál número estamos visualizando la raíz cuadrada representada en el lado de este cuadrado?
- Para responder a esta pregunta vamos a elevar 15 a la dos, porque la figura que nos presentan es un cuadrado, tal como vimos en los ejemplos que colocamos en apartados anteriores.
- Por tanto, el lado de este cuadrado representa la raíz cuadrada de 225.
- Resuelve las siguientes operaciones:
| OPERACIÓN | SOLUCIÓN |
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇

Definición de raíz cuadrada

Partes de la raíz cuadrada

Relación entre potencias y raíces cuadradas

Aclaraciones sobre las raíces cuadradas

Cálculo de raíces cuadradas

Problemas con raíces cuadradas

Definición de raíz cuadrada

Partes de la raíz cuadrada

Relación entre potencias y raíces cuadradas

Aclaraciones sobre las raíces cuadradas

Cálculo de raíces cuadradas

Problemas con raíces cuadradas