Propiedad distributiva
La propiedad distributiva es una propiedad muy importante en la matemática porque nos permite relacionar dos operaciones fundamentales, como son la multiplicación y la división.
Dominar la propiedad distributiva es fundamental para comprender conceptos algebraicos e incluso geométricas que tienen relación con ella. Los súper conocidos productos notables se basan en esta importantísima propiedad.
En este artículo conocerás qué es la propiedad distributiva de la multiplicación y qué es la propiedad distributiva de la división. También encontrarás ejemplos, ejercicios y problemas que se resuelven aplicando esta propiedad.
¿Qué es la propiedad distributiva?
Empecemos por el principio. En los números naturales el verdadero nombre de esta propiedad es:
Propiedad distributiva de la multiplicación con respecto a la adición (suma).
o
Propiedad distributiva de la multiplicación con respecto a la sustracción (resta).
Y es que esta propiedad relaciona la multiplicación con la adición (y con la sustracción) de la siguiente manera:
| Propiedad distributiva de la multiplicación | |
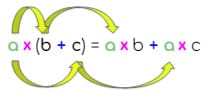 | 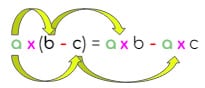 |
| Con respecto a la adición (suma) | Con respecto a la sustracción (resta) |
Si lo decimos con palabras, la propiedad distributiva de la multiplicación nos dice que:
| Propiedad distributiva de la multiplicación | |
| Con respecto a la adición (suma) | Con respecto a la sustracción (resta) |
| El producto de a por (b + c) es igual al producto de a por b más el producto de a por c. | El producto de a por (b – c) es igual al producto de a por b menos el producto de a por c. |
Como puedes observar, el factor a que multiplica la adición (o la sustracción) de los dos números b y c “se distribuye” multiplicando a ambos sumandos en el otro lado de la igualdad. Y se mantiene la operación de adición (o sustracción) entre los nuevos sumandos a x b y a x c.
Verifiquemos la propiedad con estos números:
- Caso 1: Propiedad distributiva de la multiplicación con respecto a la adición o suma
| 3 x (4 + 2) | 3 x (4 + 2) = 3 x 4 + 3 x 2 |
| 3 x 6 | 12 + 6 |
| 18 | 18 |
En ambos casos obtenemos como resultado 18, por lo que se verifica la propiedad distributiva.
- Caso 2: Propiedad distributiva de la multiplicación con respecto a la sustracción o resta
| 8 x (10 – 5) | 8 x (10 – 5) = 8 x 10 + 8 x 5 |
| 8 x 5 | 80 – 40 |
| 40 | 40 |
En los dos casos tuvimos como resultado 40, verificando así la propiedad distributiva.
Ejemplos de la propiedad distributiva de la multiplicación
En esta sección verás ejemplos de la propiedad distributiva de la multiplicación que te permitirán comprenderla aún mejor.
- Ejemplo 1:
- Tenemos la siguiente operación:
12 x (5 +4)
- Para resolverla usando la propiedad distributiva aplicamos los siguientes pasos:
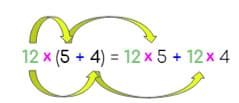 | Distribuimos el factor 12 a ambos sumandos y conservamos el signo “+” |
| = 60 + 48 | Resolvemos las multiplicaciones en cada sumando. |
| = 108 | Resolvemos la adición. |
- Ejemplo 2:
- Dada la operación:
25 x (7 – 2)
- La resolveremos usando la propiedad distributiva paso a paso:
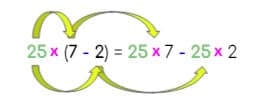 | Distribuimos el factor 25 a ambos términos de la sustracción y conservamos el signo «-«. |
| = 175 – 50 | Resolvemos las multiplicaciones en cada término. |
| = 125 | Resolvemos la sustracción. |
- Ejemplo 3
- En este ejemplo veremos cómo se aplica la propiedad distributiva para “sacar” el factor común de dos términos de una adición.
- Para ello debemos ver la propiedad distributiva reconociendo que la igualdad es bidireccional, es decir, que funciona de izquierda a derecha y de derecha a izquierda.
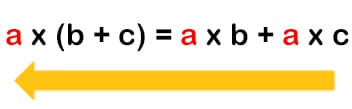
- Entonces la propiedad distributiva nos queda así:
a x b + a x c = a x (b + c)
- Observa cómo se aplica en la siguiente adición:
12 + 15
- Para poder aplicar la propiedad distributiva cada uno de los sumandos deben estar expresados como una multiplicación, y deben tener un factor común. En este caso,
12 = 3 x 4 y 15 = 3 x 5
Entonces, podemos reescribir la adición original así, y nos queda factorizada para poder aplicar la propiedad distributiva:
12 + 15 = 3 x 4 + 3 x 5
12 + 15 = 3 x (4 + 5)
Ejemplos de la propiedad distributiva en la división
La propiedad distributiva de la división tiene una característica especial para que pueda cumplirse, y es que el divisor de la adición o de la sustracción siempre estará a la derecha.
Es decir:
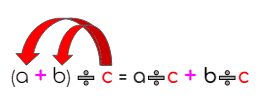
Veamos cómo aplicar esta propiedad en la siguiente operación:
(24 + 8) ÷ 2
Mira el paso a paso
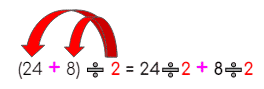 | Distribuimos el divisor a ambos sumandos. |
| (24 + 8) ÷ 2 = 12 +4 | Dividimos cada sumando entre el divisor. |
| (24 + 8) ÷ 2 = 16 | Realizamos la suma del paréntesis y dividimos entre dos. |
Vamos a comprobar esta propiedad. Es decir, resolveremos primero la operación entre paréntesis y luego dividimos para saber si obtendremos así el mismo resultado.
| (24 + 8) ÷ 2 = 32 ÷ 2 | Sumamos los términos dentro del paréntesis. |
| (24 + 8) ÷ 2 = 16 | Dividimos el resultado entre 2. |
| Nos da el mismo resultado por lo que la propiedad se verifica. | |
- Veamos otro ejemplo de la propiedad distributiva de la división:
(45 – 39) ÷ 3
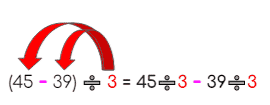 | Distribuimos el divisor a ambos términos de la resta. |
| (45 – 39) ÷ 3 = 15 – 13 | Dividimos cada término entre el divisor. |
| (45 – 39) ÷ 3 = 2 | Realizamos la resta. |
Ejercicios que se resuelven aplicando la propiedad distributiva
En este apartado te presentamos 3 ejercicios que se resuelven aplicando la propiedad distributiva de la multiplicación con respecto a la adición o la sustracción. Presta atención al paso a paso que te presentamos sobre cómo resolver este tipo de ejercicios.
- Resuelve aplicando la propiedad distributiva de la multiplicación con respecto a la adición o la sustracción dependiendo del caso.
| a | 3 x (12 + 5) = 3 x 12 + 3 x 5 | b | 9 x (10 – 2) = 9 x 10 – 9 x 2 |
| = 36 + 15 | = 90 – 18 | ||
| = 51 | = 72 |
| c | (3 + 8) x 6 = 3 x 6 + 8 x 6 | d | (13 – 3) x 12 = 12 x 12 – 3 x 12 |
| = 18 + 48 | = 144 – 36 | ||
| = 66 | = 108 |
| e | 7 x (9 + 2 – 5) = 7 x 9 + 7 x 2 – 7 x 5 | f | (8 – 3 + 11) x 4 = 8 x 4 – 3 x 4 + 11 x 4 |
| = 63 + 14 – 35 | = 32 – 12 + 44 | ||
| = 77 – 35 | = 20 – 44 | ||
| = 42 | = 64 |
- Aplica la propiedad distributiva para sacar el factor común.
- Antes de comenzar a realiza los ejercicios recuerda que:
- En una operación como 2 x 6 + 2 x 5, hay dos multiplicaciones que son: 2 x 6 y 2 x 5. En ambas el 2 es un factor común.
- Lo que nos permite escribir la operación 2 x 6 + 2 x 5 como 2 x ( 6 + 5).
- Esto es posible porque sacamos el 2 como factor común y aplicamos la propiedad distributiva.
- Ahora que ya recordamos cómo funciona el factor común, vamos a realizar algunos ejercicios.
- Antes de comenzar a realiza los ejercicios recuerda que:
- 5 x 9 + 5 x 7 + 5 x 2 = 5 x (9 + 7 + 2)
- 8 x 7 + 8 x 1 + 8 x 11 + 8 x 3 = 8 x (7 + 1 + 11 + 3)
- 9 x 6 + 4 x 6 + 7 x 6 = (9 + 4 + 7) x 6
- 3 x 20 + 3 x 30 – 3 x 10 = 3 x (20 + 30 – 10)
- En ocasiones podemos utilizar la propiedad distributiva para resolver mentalmente y con gran velocidad multiplicaciones como 5 x 12.
- Para multiplicar mentalmente 5 x 12, podemos descomponer aditivamente el 12 de la siguiente manera:
5 x 12 = 5 x (10 + 2)
= 5 x 10 + 5 x 2
= 50 + 10
= 60
- En este caso hemos escrito 12 como 10 + 2, porque para nuestra mente es más sencillo multiplicar primero por 10 y luego por 2 que multiplicar por 12.
- En este ejemplo primero realizamos la descomposición aditiva del 12, y luego aplicamos la propiedad distributiva.
A continuación, realizaremos algunos ejercicios como el que acabamos de ver. Recuerda que esto lo debes practicar primero por escrito y luego hacerlo sólo con tu mente:
| 8 x 11 = 8 x (10 + 1) | 15 x 12 = (10 + 5) x 12 |
| = 80 + 8 | = 120 + 60 |
| = 88 | = 180 |
| 6 x 13 = 6 x (10 + 3) | 7 x 17 = 7 x (10 + 7) |
| = 60 + 18 | = 70 + 49 |
| = 78 | = 119 |
Te dejamos unas fichas para que tú también realices ejercicios con la propiedad distributiva.
Problemas que se resuelven aplicando la propiedad distributiva
- Le he regalado a cada uno de mis tres hijos unas zapatillas de 68 €, unas camisas de 55 € y unos vaqueros de 70 €. ¿Cuánto gasté en regalos para mis hijos?
- Para resolver este problema utilizaremos la propiedad distributiva de la multiplicación con respecto a la adición.
- Sabemos que el padre compró 3 zapatos de 68 € cada uno, 3 camisas de 55 € cada una y 3 vaqueros de 70 € cada uno.
- Para ir traduciendo esta información al lenguaje matemático decimos que el papá compró:
3 de 68, 3 de 55 y 3 de 70.
- Para calcular cuánto gastó el padre en regalos, podemos escribirlo así:
3 x (68 + 55 + 70)
- Ahora aplicamos la propiedad distributiva de la multiplicación con respecto a la adición:
3 x (68 + 55 + 70) = 3 x 68 + 3 x 55 + 3 x 70
= 204 + 165 + 210
= 579
- Concluimos que el papá gastó 579 € en regalos para sus hijos.
- En una empresa comercial hay 5 ejecutivos de ventas y 5 asesores de marketing. Si los ejecutivos de venta cobran 35 € y los asesores de marketing 40 € diarios. ¿Cuánto cobran entre todos diariamente?
- Para resolver este problema utilizaremos la propiedad distributiva. Veamos:
- El factor que se repite es el 5, por esa razón escribimos lo siguiente:
5 x (35 + 40)
- Resolviendo esta operación tenemos:
5 x (35 + 40) = 5 x 35 + 5 x 40
= 175 + 200
= 375
- Entre todos diariamente cobran 375.
Antes de terminar, te dejamos unas actividades para ver un poquito más la aplicación de esta propiedad.
Selecciona un juego 👇 👇 👇

Propiedad distributiva - 1

Propiedad distributiva - 2

Propiedad distributiva - 3

Cuestionario

Propiedad distributiva - 1

Propiedad distributiva - 2

Propiedad distributiva - 3

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.




