En este artículo te enseñamos en qué consiste la propiedad asociativa y cómo se aplica para la suma y la multiplicación. Te damos el paso a paso de cómo utilizar esta propiedad para resolver con rapidez y eficacia problemas y ejercicios.
También te explicamos cómo la propiedad asociativa está presente cuando vas al mercado, resuelves problemas de geometría o te inicias en el estudio del álgebra.
¿Qué es la propiedad asociativa?
La asociativa es una propiedad que se aplica en la adición y la multiplicación. Esta propiedad nos dice que, cuando hay tres o más números en cualquiera de estas dos operaciones, el resultado no se ve afectado por la forma en la que son agrupados los números.
Es decir, sin importar cuál sea el par de sumandos o factores que se escoja de primero para sumar o multiplicar, las operaciones darán siempre el mismo resultado.
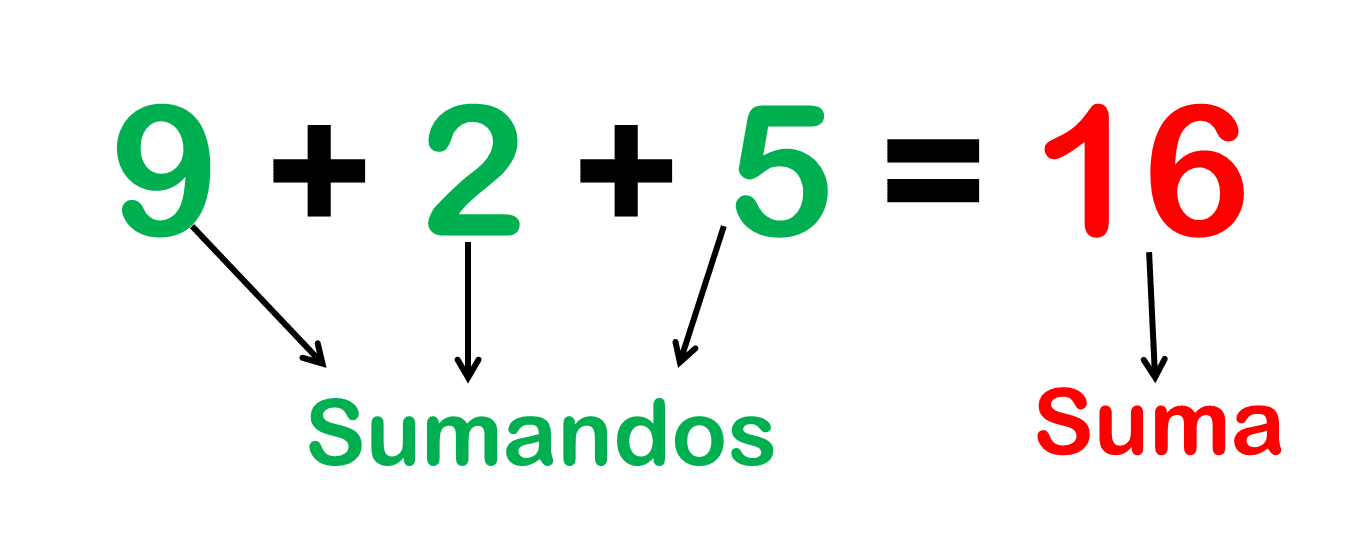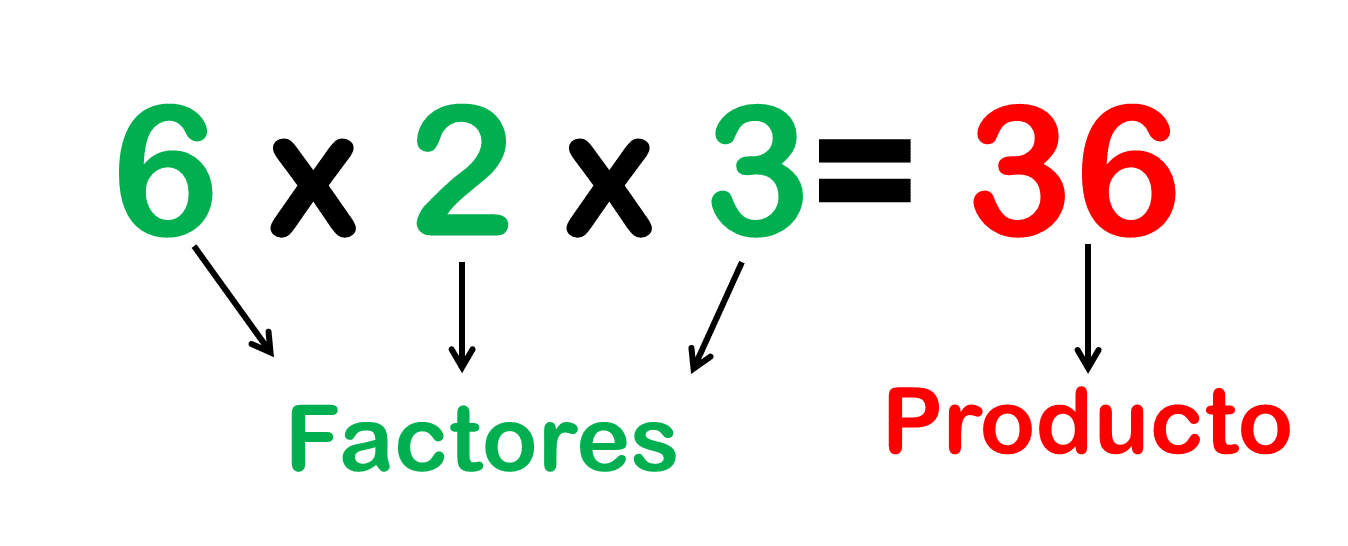¿Qué sumandos agruparías primero en esta adición?
¿Qué factores multiplicarías primero 6 x 2 o 2 x 3?
La propiedad asociativa es indispensable para sumar o multiplicar tres o más números. Por la manera en la que se definen estas dos operaciones, primero se deben agrupar dos números y luego adicionar o multiplicar el tercer número.
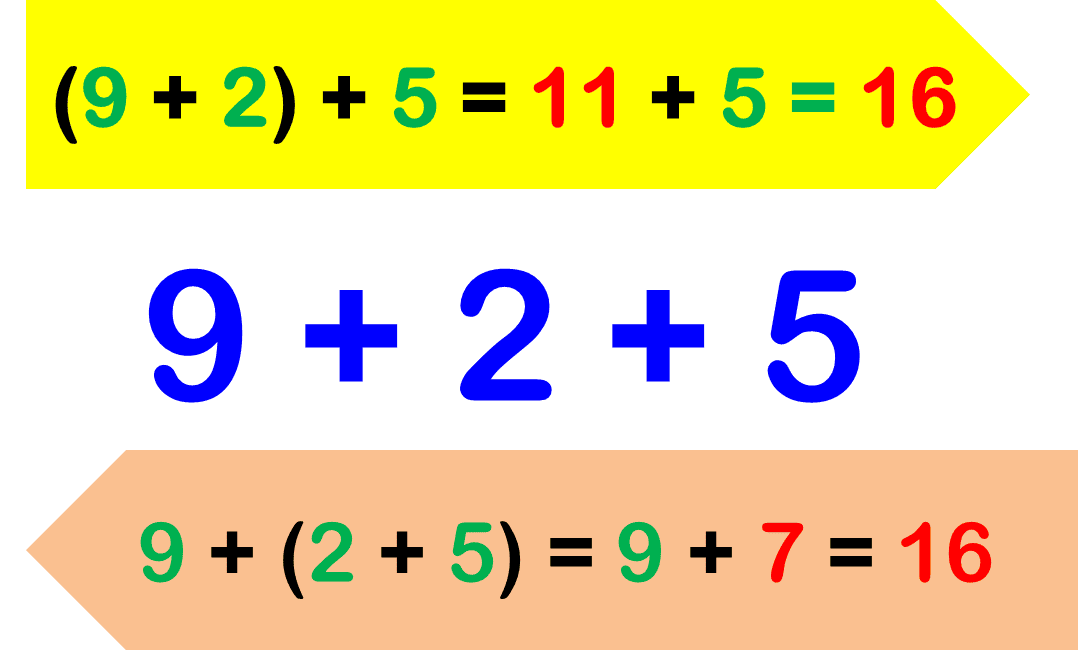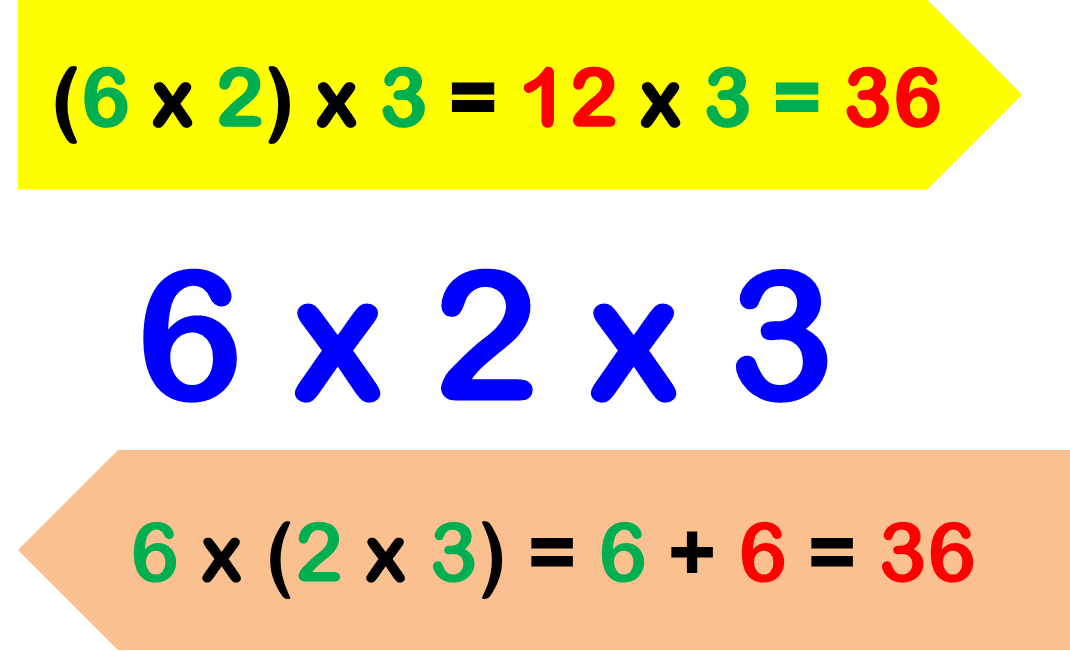Se obtiene la misma suma al asociar de dos maneras distintas.
Se obtiene el mismo producto sin importar qué par de números agrupemos primero.
No es posible realizar la adición o multiplicación de tres o más números sin aplicar la propiedad asociativa.
Podrás comprender mejor esta propiedad en general, antes de pasar a verla para cada operación, realizando la siguiente ficha que te proponemos.
Propiedad asociativa de la suma (de la adición)
Cuando se trata de la adición, la propiedad asociativa nos dice que la manera en la que se agrupan los sumandos no cambia el resultado final de la operación.
La propiedad asociativa de la adición nos garantiza que sin importar la forma en la que se junten los sumandos, la suma final siempre será la misma.
La única forma de hacer una adición como esta:
7 + 9 + 10
es aplicando la propiedad asociativa.
Veamos:
Primero debemos asociar un par de sumandos para obtener una suma parcial (un número):
(7 + 9) + 10
7 + (9 + 10)
Seguidamente, esa suma parcial la adicionamos al otro sumando para obtener la suma o resultado final:
16 + 10
7 + 19
26
26
La propiedad asociativa y su aplicación en el mercado.
Ejemplos de la propiedad asociativa de la suma
A continuación te presentamos 3 interesantes ejemplos en los que se aplica la propiedad asociativa de la adición.
Verifica que se cumpla la propiedad asociativa en la siguiente adición.
16 + 8 + 5
Veamos:
(16 + 8) + 5
16 + (8 + 5)
24 + 5
16 + 13
29
29
Sabiendo que a = 2, b = 5 y c = 8, comprueba que (a + b) + c = a + (b + c).
Lo primero que haremos será sustituir los valores de a, b y c en (a + b) + c y a + (b + c)
(a + b) + c
a + (b + c)
(2 + 5) + 8
2 + (5 + 8)
Ahora resolveremos las operaciones que nos quedaron después de sustituir los valores de a, b y c.
(2 + 5) + 8
2 + (5 + 8)
7 + 8
2 + 13
15
15
Al resolver las operaciones, que nos quedan en ambos lados de la igualdad, obtenemos que el resultado es 15 en los dos casos. Por esta razón (a + b) + c = a (b + c).
El perímetro de un triángulo se define como la suma de las longitudes de los tres lados. Conociendo esto vamos a calcular el perímetro del siguiente triángulo:
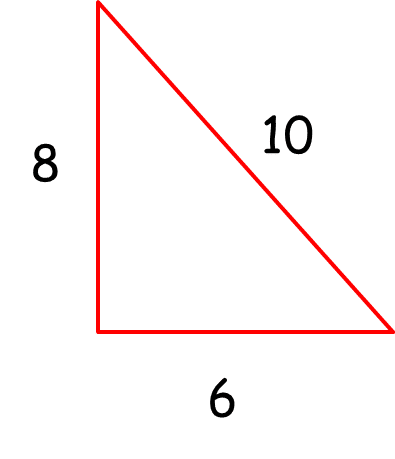
Este triángulo es rectángulo y la longitud de sus lados son 6, 8 y 10. Calculemos su perímetro utilizando cualquiera de las formas que vemos en la tabla inferior:
En este caso sumaremos primero la longitud de los dos catetos y luego le agregaremos la longitud de la hipotenusa:
Aquí primero sumaremos la longitud de uno de los catetos con la longitud de la hipotenusa y al resultado le sumamos la longitud del otro cateto:
(6 + 8) + 10
6 + (8 + 10)
14 + 10
6 + 18
24
24
En los dos casos el resultado es 24. Esto es así gracias a la propiedad asociativa de la adición.
El perímetro del triángulo de los lados 6, 8, 10 es 24.
Propiedad asociativa de la multiplicación
La propiedad asociativa de la multiplicación nos permite encontrar el producto al multiplicar más de dos números en una operación que nos hayan planteado.
Porque para poder resolver multiplicaciones como esta:
2 x 5 x 3
Es necesario asociar primero un par de factores para obtener un producto(un número):
(2 x 5) x 3
2 x (5 x 3)
Y luego, este producto lo multiplicamos por el otro factor para obtener el resultado final:
(2 x 5) x 3
2 x (5 x 3)
10x 3
2 x 15
30
30
Y es ahí donde radica la importancia de la propiedad asociativa.
La propiedad asociativa de la multiplicación nos asegura que sin importar cómo agrupemos los factores, el producto final siempre es el mismo.
Veamos cómo usan Paula y Diego la propiedad asociativa para resolver esta multiplicación:
2 x 4 x 10
Ejemplos de la propiedad asociativa de la multiplicación
Aquí verás algunos ejemplos de la propiedad asociativa de la multiplicación:
Ejemplo 1
Verifica la propiedad asociativa con la siguiente multiplicación:
25 x 3 x 2
Veamos:
(25 x 3) x 2
25 x (3 x 2)
75 x 2
25 x 6
150
150
En ambos casos obtenemos 150, sin importar si agrupamos los dos primeros factores o los dos segundos factores. Por ello se verifica la propiedad asociativa.
Ejemplo 2
Tenemos estos dos prismas rectangulares:
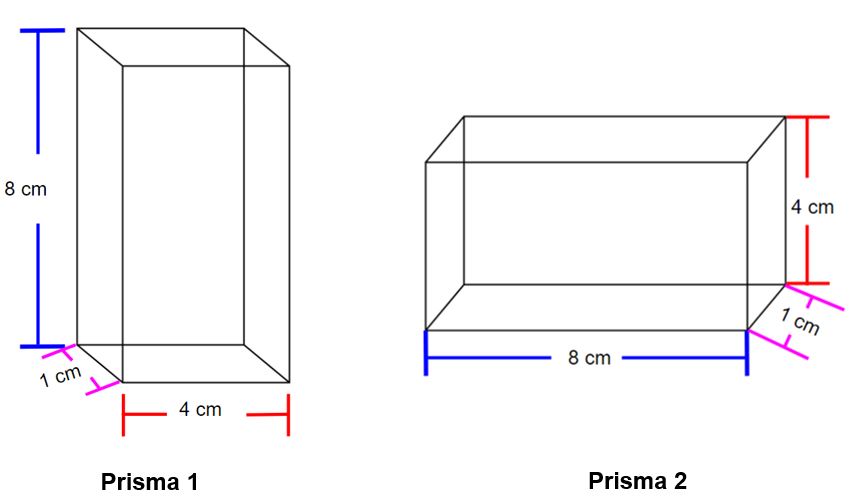
Veamos cuál es el volumen de cada uno sabiendo que el volumen de un prisma rectangular es igual al área de la base del prisma por la altura del prisma.
Prisma 1
Prisma 2
El área de la base del prisma 1 es 4 cm x 1 cm
La altura del prisma es 8 cm.
El volumen del prisma es:
El área de la base del prisma 2 es 8 cm x 1 cm
La altura del prisma es 4 cm.
El volumen del prisma es:
(4 cm x 1 cm) x 8 cm
(8 cm x 1 cm) x 4 cm
4 cm2 x 8 cm
8 cm2 x 4 cm
32 cm3
32 cm3
Ejemplo 3
En una distribuidora de alimentos orgánicos recibieron un cargamento de 250 cajas de legumbres y cada caja pesa 40 kilogramos. Si la distribuidora vende cada kilogramo de legumbres en 30 Euros. ¿Cuál será el monto de la venta de todo el cargamento?
Este problema podemos resolverlo de dos formas. Para ello usamos la propiedad asociativa de la multiplicación. Veamos:
Forma 1
Forma 2
Calculamos la cantidad total de kilogramos de legumbres.
Luego multiplicamos esta cantidad por el precio de venta de cada kilogramo.
Nos quedaría así:
Calculamos el precio de venta de cada caja.
Luego multiplicamos ese número por el total de cajas de legumbres que hay.
Nos quedaría de la siguiente manera:
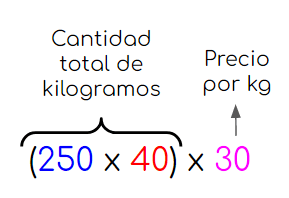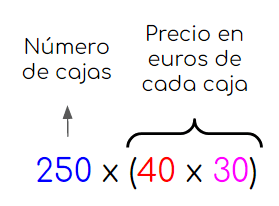Ahora resolvemos aplicando la asociatividad:
Resolvemos primero la operación entre paréntesis:
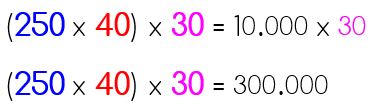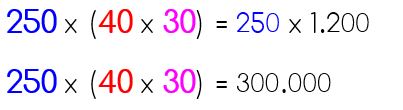Usando cualquiera de las dos formas de resolver este problema obtenemos que el monto de la venta de todo el cargamento es 300.000 euros.
Antes de concluir, te ofrecemos unas actividades para que practiques la propiedad asociativa de la multiplicación.
Selecciona un juego 👇 👇 👇
P. asociativa suma - 1
P. asociativa suma - 2
P. asociativa multiplicación - 1
P. asociativa multiplicación -2
Cuestionario
Registrado en SafeCreative.
Mª Gabriela Gracia y Darwin Silva
Profesores universitarios. Magísters en Educación Mención Enseñanza de la Matemática. Investigadores en el área de innovaciones educativas.
Registrado en SafeCreative.