Potencias de base 10
Las potencias de base diez son muy valiosas para la matemática, esto gracias a la gran utilidad que tienen.
Particularmente las potencias de base 10 de exponente entero positivo, permiten expresar de forma abreviada las unidades enteras (unidades, decenas, centenas, unidades de mil, centenas de mil,…) del Sistema de Numeración Decimal. Veamos:
| Órdenes del Sistema de Numeración Decimal | Potencia de base 10 |
| Unidad | 100 = 1 |
| Decena | 101 = 10 |
| Centena | 102 = 100 |
| Unidad de mil | 103 = 1.000 |
| Decena de mil | 104 = 10.000 |
| Centena de mil | 105 = 100.000 |
| Unidad de millón | 106 = 1.000.000 |
Por ejemplo, el número 3.000 se puede escribir como 3 x 103. Siendo 103 una manera de abreviar el orden de la unidad de mil.
Además, con este tipo de potencias podemos simplificar la escritura de números muy grandes.
Veamos:
- 7.000.000.000.000.0000 = 7 x 1015.
- 15.000.000 = 1,5 x 107.
¿Qué son las potencias de base 10?
La potencia es una operación que sirve para escribir de forma simplificada una multiplicación en la que todos sus factores son iguales. Por ejemplo:
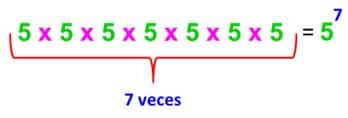
- En este caso la base de la potencia es 5 y el exponente es 7. La operación indicada es una multiplicación en la que el 5 aparece 7 veces como factor.
Ahora tenemos una potencia de base 10 y exponente 9, lo que genera una multiplicación en la que el 10 aparece 9 veces como factor.
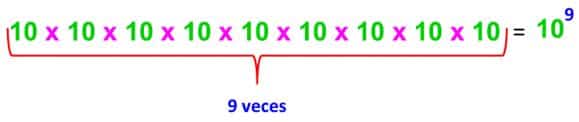
- En el caso específico de las potencias de base 10 de exponente entero positivo, el resultado queda conformado por la unidad seguida de tantos ceros como indique el exponente. Veamos:
![]()
- En este caso el resultado es igual a la unidad seguida de 9 ceros.
Ejemplos
Las potencias de base 10 de exponente entero positivo, son empleadas para expresar de forma resumida cantidades muy grandes, por lo que son muy importantes para las Ciencias de la Naturaleza, la Geografía, la Geología, la Astronomía, entre otras áreas de conocimiento.
Veamos algunos ejemplos en los que se utilizan las potencias de base 10:
- La distancia de la Tierra a la Luna es 384.000 km
- Para escribir 384.000 utilizando potencias de base 10 y un exponente entero positivo realizamos lo siguiente:
- Colocamos una coma en la primera cifra entera del número 384.000 que en este caso es el 3. Esto significa que nos movemos 5 puestos a la izquierda.

- Luego se multiplica por 105 para que el número inicial no se altere.
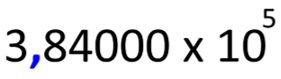
- Concluimos que la distancia de la Tierra a la Luna utilizando potencias de base 10 es 3,84 x 105 km.
- La distancia de la Tierra al Sol es de 150.000.000 km
- Vamos a realizar un proceso similar al que ejecutamos en el ejemplo anterior.
- Escribimos una coma en la primera cifra entera del número 150.000.000 que en este caso es el 1. Esto significa que nos movemos 8 puestos a la izquierda.

- A continuación se multiplica por 108 para que el número inicial no cambie.
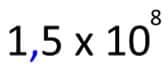
- Entonces, la distancia de la Tierra al Sol queda expresada así 1,5 x 10 8 km.
- La distancia de la Tierra a Neptuno es de 4.308.000.000 km.
- La distancia de la Tierra a Neptuno utilizando potencias de base 10 quedaría expresada así: 4,308 x 109 km.
- La edad del Sol es de aproximadamente 5 x 109 años. Sin embargo, hay cuerpos que pueden tener 4 veces la edad del Sol. ¿Cuál es la edad de estos cuerpos?
- El enunciado nos dice que la edad del Sol es aproximadamente 5 x 109 años y que existen cuerpos que tienen 4 veces la edad del Sol.
- Queremos saber cuál es la edad de esos cuerpos.
- Para responder a la pregunta es suficiente realizar la siguiente multiplicación:
![]()
- Veamos:
| Explicación | Procedimiento |
| 4 x (5 x 109) | El cuádruple de la edad del Sol |
| (4 x 5) x 109 | Agrupamos los coeficientes 4 y 5 |
| 20 x 109 | Multiplicamos 4 por 5 |
| (2 x 10) x 109 | Escribimos 20 como 2 x 10 |
| 2 x (10 x 109) | Agrupamos las potencias de base 10 |
| 2 x 1010 | Multiplicamos potencias de igual base |
- Concluimos que la edad aproximada de los cuerpos es 2 x 1010
Operaciones con potencias de base 10
Uno de los usos de las potencias de base 10 es realizar operaciones de forma sencilla, porque las potencias de base 10 nos sirven para escribir números muy grandes o números muy pequeños de forma simplificada, tal como vimos anteriormente.
En este apartado aprenderemos a sumar, restar, multiplicar y dividir con potencias de base 10.
Suma y resta de potencias de base 10
Para sumar potencias de base 10 tenemos que fijarnos en la potencia de 10. Podemos tener dos casos:
- Ambos términos tienen la misma potencia de 10.
![]()
- Los términos tienen distintas potencias de 10.
![]()
Caso 1: Ambos términos tienen la misma potencia de 10.
- Veamos el primer ejemplo de cómo sumar cuando ambos términos tienen la misma potencia de 10:
![]()
- En este caso, ambos términos tienen la potencia:
![]()
- Lo que hacemos es sumar los coeficientes de cada término y colocamos la misma potencia:
![]()
- Mira este otro ejemplo del mismo caso, pero esta vez con la resta:
![]()
- En este ejemplo los dos términos tienen la potencia:
![]()
- Lo que hacemos es sumar los coeficientes de cada término y colocamos la misma potencia:
![]()
Caso 2: Los términos tienen distintas potencias de 10.
- Observa este primer ejemplo con adición:
![]()
- Los términos tienen distintas potencias de base 10. En este caso:
![]()
- Como ves, los exponentes de las potencias son 6 y 5.
- Lo primero que haremos es escribir los términos de forma que tengan el mismo exponente.
- Tomamos el término que tenga la potencia de 10 con menor exponente, que en este es:
![]()
- Y lo llevaremos al exponente 6. Para ello, vemos cuál es la diferencia entre 5 y 6 en la recta.
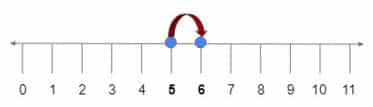
- La diferencia es 1 unidad hacia la derecha.
- Nos tenemos que mover 1 lugar a la derecha para pasar de 5 a 6. Entonces, vamos a mover la coma 1 lugar hacia la izquierda.
- Y, además, sumamos 1 al exponente de la potencia base 10. Nos queda así:
![]()
| Fíjate que ambas expresiones son equivalentes al desarrollarlas: |
| 2,1 x 105 = 210.000 |
| 0,21 x 106 = 210.000 |
- Ahora sí podemos reescribir el término para realizar la adición:
![]()
- Sumamos los coeficientes y dejamos la misma potencia de base 10.
![]()
- Veamos otro ejemplo con la sustracción:
![]()
- Los exponentes son 4 y 2.
- Tomamos el término con el exponente menor de las potencias base 10 (el 2) y buscamos la diferencia entre ese exponente y el mayor (el 4).
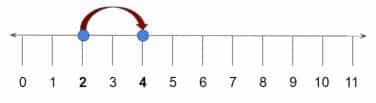
- Para pasar de 2 a 4 nos movemos 2 unidades a la derecha, entonces movemos la coma 2 lugares a la izquierda. Nos queda así:
![]()
| Fíjate que ambas expresiones son iguales: |
| 3,4 x 102 = 340 |
| 0,034 x 104 = 340 |
- Ahora reescribimos el término y sí podemos restar:
![]()
- Restamos los coeficientes y dejamos la misma potencia base 10.
![]()
Multiplicación de potencias de base 10
La multiplicación de potencias de base 10 es otra de las operaciones que se usan bastante, especialmente en las Ciencias de la Naturaleza porque trabajan con números muy pequeños o muy grandes.
Multiplicar potencias de base 10 es mucho más fácil que sumarlas o restarlas porque no tenemos que preocuparnos por los exponentes de la potencia.
Ahora bien, para multiplicar potencias de base 10 es necesario recordar una propiedad de la potenciación, ya que multiplicamos potencias de bases iguales.
| Para multiplicar potencias de igual base se conserva la bases y se suman los exponentes: |
| an x am = an + m |
| Ejemplo: 105 x 103 = 105+3 = 108 |
Para resolver una multiplicación con potencias de base 10 debemos:
- Multiplicar los coeficientes de los factores.
- Multiplicar las potencias de base 10 aplicando la propiedad de la multiplicación de potencias de igual base.
Veamos un par de ejemplos:
- Ejemplo 1
| (2 x 103) x (3 x 1011) | |
| Procedimiento | Explicación |
| (2 x 103) x (3 x 1011) = (2 x 3) x (103 x 1011) | Agrupamos los coeficientes y las potencias de base 10 |
| (2 x 103) x (3 x 1011) = (6) x (103 x 1011) | Multiplicamos los coeficientes |
| (2 x 103) x (3 x 1011) = 6 x (103 + 11) | Multiplicamos las potencias de base 10 sumando los exponentes |
| (2 x 103) x (3 x 1011) = 2 x 1014 | Resultado |
- Ejemplo 2
| (3 x 106) x (1,5 x 1015) | |
| Procedimiento | Explicación |
| (3 x 106) x (1,5 x 1015) = (3 x 1,5) x (106 x 1015) | Agrupamos los coeficientes y las potencias de base 10 |
| (3 x 106) x (1,5 x 1015) = (4,5) x (106 x 1015) | Multiplicamos los coeficientes |
| (3 x 106) x (1,5 x 1015) = 4,5 x (106 + 15) | Multiplicamos las potencias de base 10 sumando los exponentes |
| (3 x 106) x (1,5 x 1015) = 4,5 x 1021 | Resultado |
División de potencias de base 10
Al igual que para la multiplicación, para dividir potencias de base 10 debemos recordar una propiedad de la división de potencias de bases iguales.
| Para dividir potencias de igual base se conserva la base y se restan los exponentes: |
| an ÷ am = an – m |
| Ejemplo: 108 ÷ 102 = 108-2 = 106 |
Para dividir potencias de base 10 hacemos lo siguiente:
- Dividir los coeficientes de los factores.
- Dividir las potencias de base 10 aplicando la propiedad de la división de potencias de igual base.
A continuación te presentamos algunos ejemplos que hemos resuelto paso a paso:
- Ejemplo 1:
| (9 x 1012) ÷ (3 x 105) | |
| Procedimiento | Explicación |
| (9 x 1012) ÷ (3 x 105) = (9 ÷ 3) x (1012 ÷ 105) | Agrupamos los coeficientes y las potencias de base 10 |
| (9 x 1012) ÷ (3 x 105) = (3) x (1012 ÷ 105) | Dividimos los coeficientes |
| (9 x 1012) ÷ (3 x 105) = 3 x (1012-5) | Dividimos las potencias de base 10 restando los exponentes |
| (9 x 1012) ÷ (3 x 105) = 3 x 107 | Resultado |
- Ejemplo 2
| (3 x 108) ÷ (1,5 x 102) | |
| Procedimiento | Explicación |
| (3 x 108) ÷ (1,5 x 102) = (3 ÷ 1,5) x (108 ÷ 102) | Agrupamos los coeficientes y las potencias de base 10 |
| (3 x 108) ÷ (1,5 x 102) = (2) x (108 ÷ 102) | Dividimos los coeficientes |
| (3 x 108) ÷ (1,5 x 102) = 2 x (108-2) | Dividimos las potencias de base 10 restando los exponentes |
| (3 x 108) ÷ (1,5 x 102) = 2 x 106 | Resultado |
- Ejemplo 3
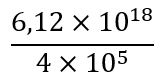 | |
| Procedimiento | Explicación |
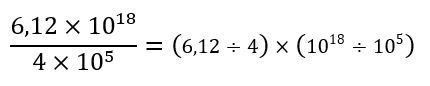 | Agrupamos los coeficientes y las potencias de base 10 |
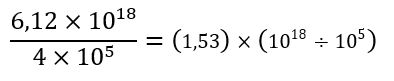 | Dividimos los coeficientes |
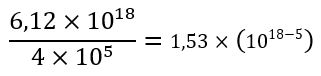 | Dividimos las potencias de base 10 restando los exponentes |
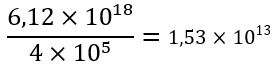 | Resultado |
Por último, aquí tienes unas actividades para que sigas practicando:
Selecciona un juego 👇 👇 👇

Potencias de base 10 - 1

Potencias de base 10 - 2

Potencias de base 10 - 3

Potencias de base 10 - 1

Potencias de base 10 - 2

Potencias de base 10 - 3
![]() Registrado en SafeCreative.
Registrado en SafeCreative.



