Potencias cuadradas y cúbicas
Las potencias cuadradas y cúbicas, también conocidas como cuadrados y cubos de un número, son muy comunes en situaciones de la vida cotidiana. Esto es porque las ideas de cuadrado y de cubo están muy relacionadas con las nociones espaciales y geométricas de área y de volumen.
En este artículo aprenderás todo lo que necesitas sobre potencias cuadradas y cúbicas: qué son, ejemplos y ejercicios resueltos.
¿Qué es una potencia cuadrada o número al cuadrado?

La expresión anterior puede leerse como:
“a a la dos” o “a al cuadrado”
Y se resuelve así:
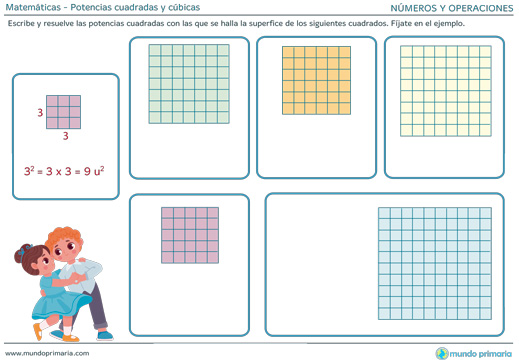
a² = a x a
- Por ejemplo:
- Tres al cuadrado, o tres a la dos, se resuelve así:
3² = 3 x 3 = 9
Podemos decir que 9 es el cuadrado de 3.
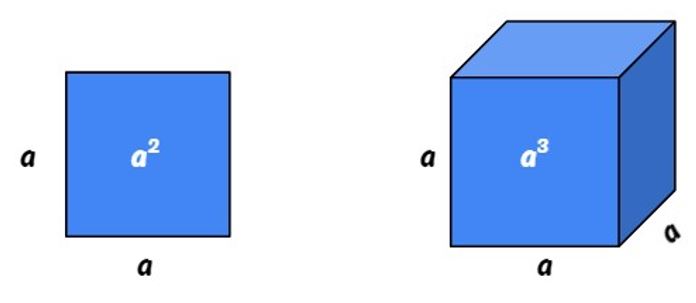
Representación geométrica de la potencia cuadrada
La potencia cuadrada puede tener una representación geométrica. Veamos:
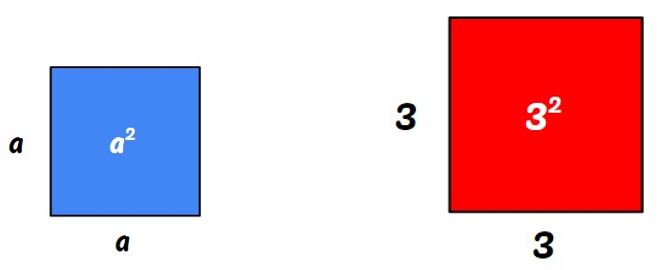
- El área del cuadrado de lado a es igual a a2 .
- El área del cuadrado de lado 3 es igual a 32= 33 = 9
Por esta representación geométrica es que la potencia con exponente 2 se llama también número al cuadrado.
Ejemplos de potencias cuadradas
Los usos de las potencias cuadradas dentro de la matemática y en la vida cotidiana son muchos. Aquí te daremos un par de ejemplos:
Ejemplo 1: Los números cuadrados
En matemática los números cuadrados son aquellos que se obtienen como resultado de elevar un número a la dos.
Estos números tienen una representación geométrica en forma de cuadrados. Veamos:
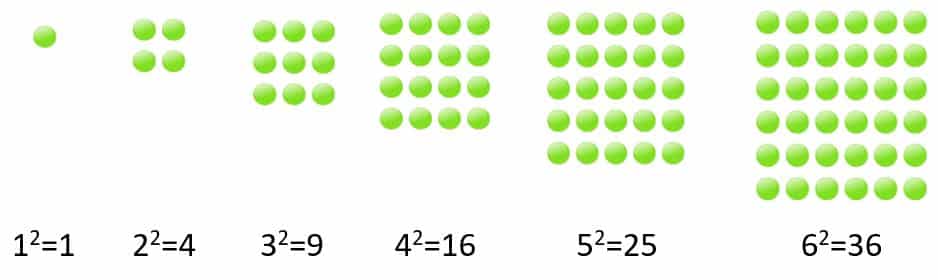
Ejemplo 2: Área de superficies
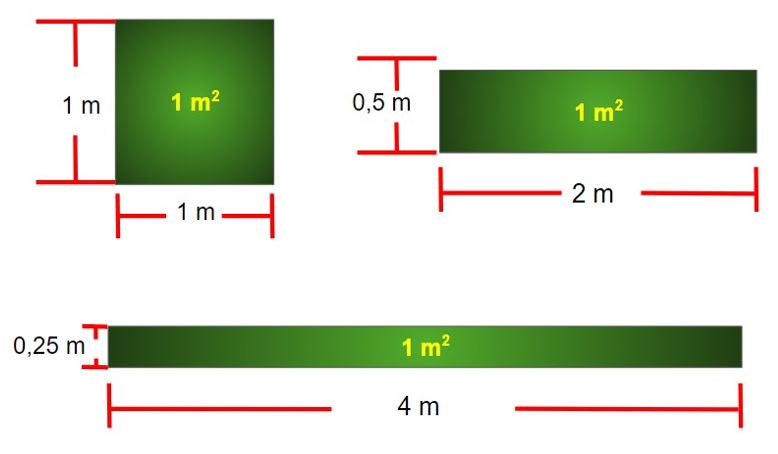
En muchas ocasiones habrás oído hablar de metros cuadrados (m2), es una expresión que se usa tanto en los libros de matemática como en la construcción, la arquitectura, etc. Pero sabías que esta expresión no siempre se refiere a superficies con forma de cuadrado.
A continuación te dejamos algunos ejemplos de superficies cuya área es de 1m2 .
Ejercicios resueltos de potencias cuadradas
En este apartado resolveremos paso a paso ejercicios y problemas con potencias cuadradas
- ¿Cuál es el cuadrado de 11?
- Lo que queremos calcular es 112, y esto es:
11² = 11 x 11 = 121
El cuadrado de 11 es 121.
- ¿25 es el cuadrado de qué número?
- En este caso queremos saber qué número multiplicado por sí mismo nos da 25. Para ello podemos ir probando con cada número:
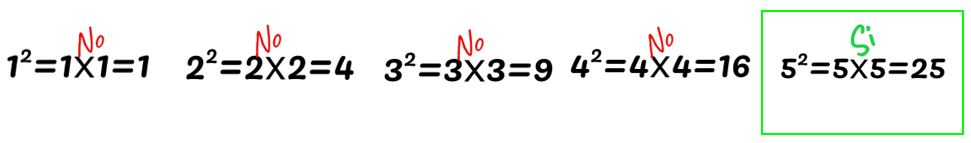
Como puedes observar, 25 es el cuadrado de 5.
- Al cuadrado de un número le hemos restado 2 y nos da 14. ¿Cuál es el número?
- Sabemos que 14 es el cuadrado del número que estamos buscando disminuido en 2.
- Esto quiere decir que al cuadrado le han restado 2 unidades.
- Entonces, para saber cuál es el cuadrado del número debemos sumarle dos unidades a 14.
14 + 2 = 16
- El cuadrado del número es 16.
- Ahora, para conseguir el número que estamos buscando, vamos a ver qué número elevado al cuadrado da 16.

Podemos concluir que el número que estamos buscando es 4.
Puedes practicar las potencias cuadradas con las siguientes recursos:
¿Qué es una potencia al cubo?
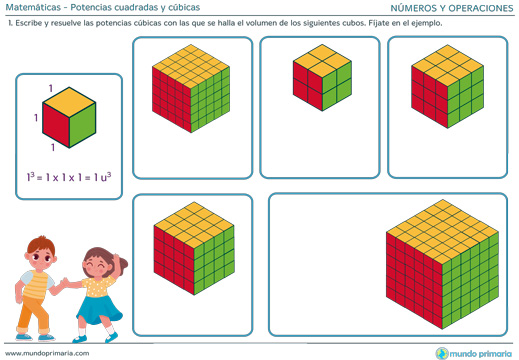
Cuando multiplicamos 7 x 7 x 7 decimos 7 elevado a la 3 o 7 al cubo.
Como el 7 aparece tres veces como factor de la multiplicación podemos escribirlo así:
73= 7 x 7 x 7 = 343
Al resultado 343 lo llamamos cubo del número 7. También se acostumbra a decir que 343 es un número cúbico o sencillamente que 343 es un cubo.
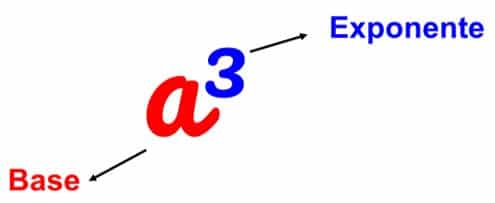
La expresión anterior puede leerse como:
“a a la tres” o “a al cubo”
Representación geométrica de la potencia al cubo
La potencia cúbica puede tener una representación geométrica.
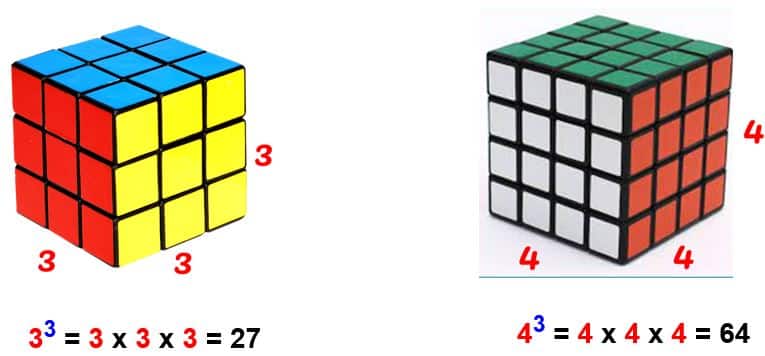
La imagen que vemos a continuación es del cubo de Rubik y en ella nos apoyaremos para ilustrar las potencias cúbicas. Veamos:
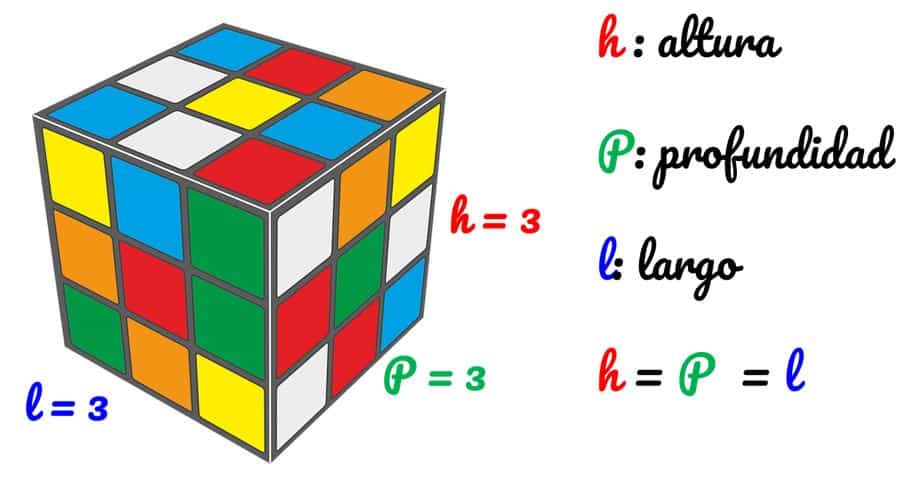
Para calcular el volumen de este cubo multiplicamos las longitudes del largo, la profundidad y la altura. Esto es:

En este caso el 27 lo podemos interpretar como los 27 cubos pequeños que forman el cubo grande.
Como en un cubo la profundidad, el largo y la altura son siempre de igual medida, entonces el volumen es una potencia al cubo. Veamos:
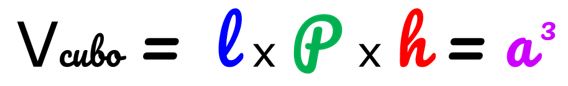
Ejemplos de potencias al cubo
- Ejemplo 1: Los cuatro primeros números cúbicos.
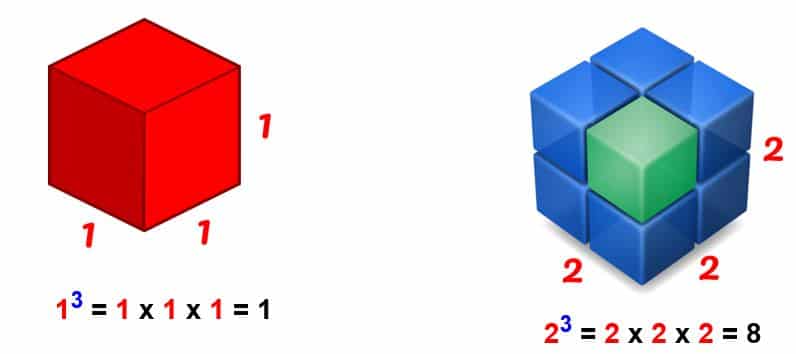
- Ejemplo 2: ¿Cuánto es 03?
0³ = 0 x 0 x 0 = 0
- Cero al cubo es siempre igual a cero. Toda potencia cuya base sea 0 da como resultado 0.
- Ejemplo 3: Calcula (5 x 2)3
- Para calcular (5 x 2)3 multiplicamos primero 5 x 2 y luego el resultado que es 10 lo elevamos al cubo. Veamos:
(5 x 2)³ = 10³ = 10 x 10 x 10 = 1.000
Ejercicios de potencias cúbicas
En este apartado resolveremos paso a paso ejercicios y problemas con potencias al cubo.
- ¿Cuál es el cubo de 12?
12³ = 12 x 12 x 12 = 1.728
El cubo de 12 es 1.728.
- ¿ 216 es el cubo de qué número?
- En este caso queremos saber qué número elevado al cubo nos da 216. Para ello podemos ir probando con cada número:
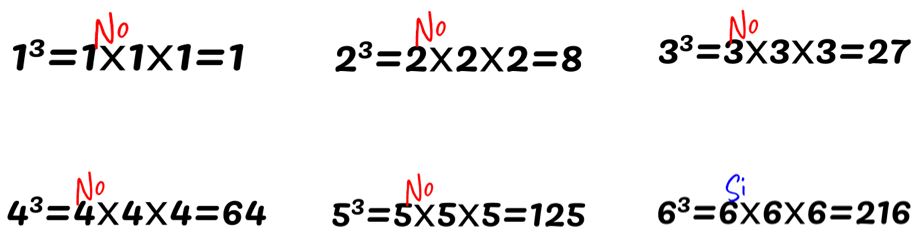
Como puedes observar, 216 es el cubo de 6.
- Al cubo de un número le hemos restado 3 y nos da 24. ¿Cuál es el número?
- Sabemos que 24 es el cubo del número que estamos buscando disminuido en 3.
- Esto quiere decir que al cubo le han restado 3 unidades.
- Para saber cuál es el cubo del número debemos sumarle tres unidades a 24.
24 + 3 = 27
El cubo del número es 27.
- Ahora, para conseguir el número que estamos buscando, vamos a ver qué número elevado al cubo da 27.
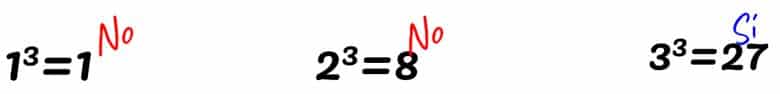
Concluimos que el número que estamos buscando es 3.
Este es un buen punto para pararnos a practicar las potencias cúbicas con las fichas que encontrarás a continuación.
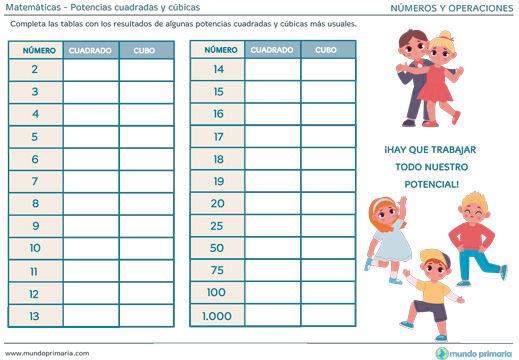
Tabla de cuadrados y cubos
En esta tabla encontrarás los cuadrados y los cubos de números que utilizamos casi a diario, y otros notables que debes siempre tener a mano y recordar.
| Número | Cuadrado | Cubo | Número | Cuadrado | Cubo | |
| 2 | 4 | 8 | 20 | 400 | 8.000 | |
| 3 | 9 | 27 | 25 | 625 | 15.625 | |
| 4 | 16 | 64 | 30 | 900 | 27.000 | |
| 5 | 25 | 125 | 35 | 1.225 | 42.875 | |
| 6 | 36 | 216 | 40 | 1.600 | 64.000 | |
| 7 | 49 | 343 | 45 | 2.025 | 91.125 | |
| 8 | 64 | 512 | 50 | 2.500 | 125.000 | |
| 9 | 81 | 729 | 60 | 3.600 | 216.000 | |
| 10 | 100 | 1.000 | 70 | 4.900 | 343.000 | |
| 11 | 121 | 1.331 | 80 | 6.400 | 512.000 | |
| 12 | 144 | 1.728 | 90 | 81.000 | 729.000 | |
| 13 | 169 | 2.197 | 100 | 10.000 | 1.000.000 | |
| 15 | 225 | 3.375 | 1.000 | 1.000.000 | 100.000.000 |
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇

Potencias cuadradas y cúbicas - 1

Potencias cuadradas y cúbicas - 2

Potencias cuadradas y cúbicas - 3

Potencias cuadradas y cúbicas - 4

Potencias cuadradas y cúbicas - 5

Potencias cuadradas y cúbicas - 6

Cuestionario

Potencias cuadradas y cúbicas - 1

Potencias cuadradas y cúbicas - 2

Potencias cuadradas y cúbicas - 3

Potencias cuadradas y cúbicas - 4

Potencias cuadradas y cúbicas - 5

Potencias cuadradas y cúbicas - 6

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.