Los números primos
Dentro de las matemáticas existe un conjunto de números muy especiales, que tienen ciertas propiedades que han intrigado durante siglos a los matemáticos. Hablamos de los números primos.
Los números primos son aquellos números, mayores que 1, que solo admiten como divisores a ellos mismos y al número 1.
Tomemos el caso del número 5. Este número es divisible por 1 y por 5.
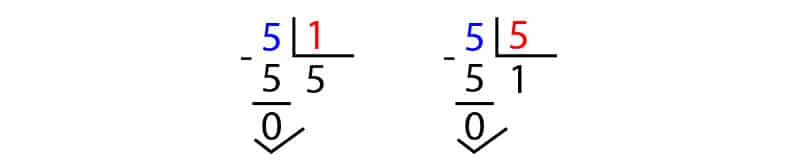
De aquí se deduce que:
- 1 divide a 5 pues el resto de su división es cero (es división exacta).
- 5 es múltiplo de 1 porque 5 = 5 x 1.
- 5 divide a 5 pues el resto de la división es cero (es exacta la división)
- 5 es múltiplo de 5 ya que 5 = 1 x 5.
Pero busquemos más divisores de 5 entre los otros números naturales menores que él.
Esto quiere decir que vamos a verificar si el 2, el 3 o el 4 dividen al número 5:
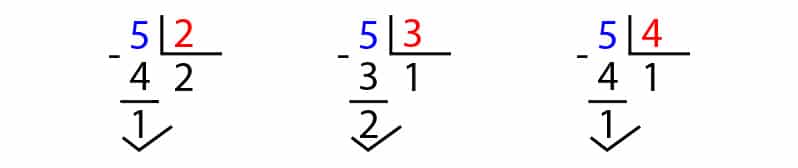
Podemos notar que:
- 2 no divide a 5 porque la división no es exacta y el resto es 1.
- 5 no es múltiplo de 2, ya que no hay ningún número natural que al multiplicarlo por 2 de como producto exactamente 5.
- 3 no divide a 5 pues tiene como resto 2, su división no es exacta.
- 5 no es múltiplo de 3, pues ningún número natural multiplicado por 3 da 5.
- 4 no divide a 5 porque la división no es exacta, y su resto es 1.
- 5 no es múltiplo de 4, ya que no existe un número natural que multiplicado por 4 de 5 como resultado.
Sabemos entonces que el 5 tiene solo dos divisores que son 1 y 5.
Por eso, 5 es un número primo, ya que solo admite como divisores al 1 y a él mismo.
Diferencia entre números primos y números compuestos
Como ves, los números primos solo tienen dos divisores, mientras que la gran mayoría de los números pueden tener muchos más divisores.
A los números que tienen más divisores que a ellos mismos y al 1 los llamamos números compuestos.
Esto también quiere decir que los números compuestos se obtienen como producto de varios factores que pueden ser distintos a él mismo o al 1.
Tomemos como ejemplo el número 6.
Como hemos visto, el 6 es divisible por sí mismo y por el 1:
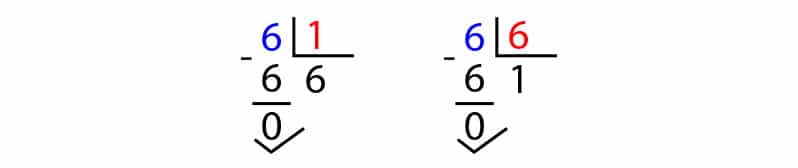
Como ya lo habíamos mencionado, todo número es divisible por 1 y por él mismo, y el número 6 no es la excepción.
Veamos ahora si el número 6 admite otros divisores además de 1 y 6.
Para ello, verificaremos si algún otro número natural menor que 6 lo divide, tal como hicimos anteriormente con el número 5:
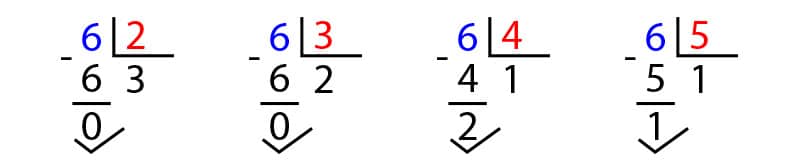
Como observamos, hay dos divisiones exactas que son 6 entre 2 y 6 entre 3.
De esto concluimos que:
- 2 divide a 6 y, lo que es igual, 6 es múltiplo de 2.
- 3 divide a 6, es decir, 6 es múltiplo de 3.
Por último, podemos decir que los divisores de 6 son el 1, el 2, el 3 y el propio 6.
De manera que 6 es un número compuesto.
Ya hemos visto la primera diferencia entre primos y compuestos:
Ahora veamos otra diferencia entre números primos y compuestos.
Como sabemos, todo número puede escribirse como una cuadrícula de filas y columnas.
Así, por ejemplo, el número 6 que hemos estado trabajando anteriormente, puede representarse de la siguiente manera:
NÚMERO 6 | |
|---|---|
 | 1 fila x 6 columnas Esta cuadrícula es de 1 x 6 |
 | 2 filas x 3 columnas Esta cuadrícula es de 2 x 3 |
 | 3 filas x 2 columnas Esta cuadrícula es de 3 x 2 |
 | 6 filas x 6 columnas Esta cuadrícula es de 6 x 1 |
El 6 tiene 4 formas de representarse de manera rectangular porque es múltiplo de 4 números que son el 1, el 2, el 3 y el 6.
Veamos ahora qué pasa cuando representamos un número primo en cuadrículas rectangulares.
Para ello tomemos como ejemplo el número 5, que hemos estado trabajando y veamos de cuántas formas podemos representarlo:
NÚMERO 5 | |
|---|---|
 | 1 fila x 5 columnas Esta cuadrícula es de 1 x 5 |
 | 5 filas x 1 columna Esta cuadrícula es de 5 x 1 |
Como puedes observar, el número 5 solo tiene 2 formas de representarse de manera rectangular porque solo es múltiplo del 1 y del 5.
Esta es otra diferencia entre primos y compuestos:
Ejemplos de números primos
Observa esta tabla con los números primos menores que 25:
| 2 | 3 | 5 |
| 7 | 11 | 13 |
| 17 | 19 | 23 |
Estos números al ser primos, como ya hemos mostrado anteriormente, solo son divisibles por ellos y por el número 1.
Para determinar si un número es primo o compuesto no es necesario dividirlo entre cada uno de sus posibles divisores y comprobar que el resto sea cero, como lo hicimos anteriormente.
Recuerda que existen los criterios de divisibilidad que te permiten saber si un número es divisible por otro, y esos criterios ayudan a determinar si un número es primo o compuesto.
Aquí presentamos un cuadro resumen de los criterios de divisibilidad del 2, 3 y 5.
Es divisible por: | Si… |
|---|---|
| 2 | El número es par, es decir, termina en 0, 2, 4, 6 u 8. |
| 3 | La suma de los dígitos del número es múltiplo de 3. |
| 5 | El número termina en 5 o en 0. |
Tomemos como ejemplo el número 10 para aplicar estos criterios y ver por qué no está en la tabla de números primos menores que 25.
- 10 es divisible por 1 y por 10, pues todo número tiene como divisores a sí mismo y al 1.
- 10 es divisible por 2, porque 10 es número par.
- 10 es divisible por 5, porque termina en 0.
Por tanto, 10 es compuesto y por eso no está en nuestra tabla de números primos menores que 25.
Ahora veamos el caso del número 7 que sí aparece en la tabla:
- 7 es divisible por 1 y por 7, porque todo número es divisible por 1 y por sí mismo.
- 7 no es divisible por 2, pues no es par.
- 7 no es divisible por 3, porque no cumple con el criterio de divisibilidad por 3.
- 7 no es divisible por 5, pues no termina ni en cero ni en 5.
- 7 no es divisible por 6 pues su división no es exacta.
De manera que el número 7 solo admite al mismo 7 y al 1 como divisores, por eso es primo y está en la tabla de los números primos menores que 25.
Criba de Eratóstenes
Un matemático y astrónomo griego, llamado Eratóstenes creó una forma de obtener los números primos. La súper conocida criba de Eratóstenes ha llegado hasta nuestros días.
Para los primeros cien números naturales, el método puede resumirse de la siguiente manera:
- Se coloca en una cuadrícula los primeros cien números naturales.
- Tachamos el número 1, por no ser ni primo ni compuesto. ¿Recuerdan por qué?
- Se continúa con el número 2, lo resaltamos y seguidamente se tachan todos los otros números múltiplos de 2, por tanto, tachamos el 4, 6, 8, 10, 12, y así sucesivamente hasta llegar al 100, que también es múltiplo de 2.
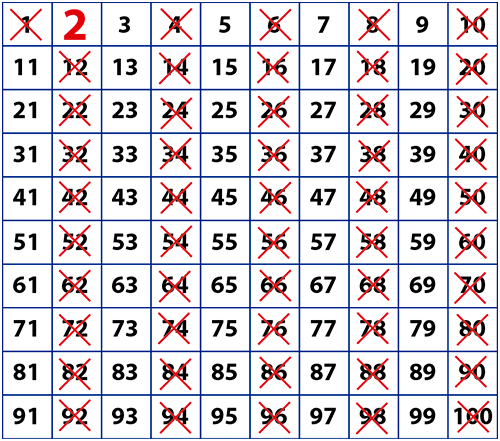
- Se sigue con el siguiente número no tachado en el cuadro, el 3, se procede a resaltarlo con el color azul como primo y se luego se tachan todos los múltiplos de 3 que están sin marcas (es decir, 9, 15, 21, 21, hasta llegar al 99 que también es múltiplo de 3). Es interesante observar que el 6, el 12 y el 18, que son múltiplos de 3, ya están tachados. Y esto se debe a que estos números son múltiplos de 2 y 3 al mismo tiempo. En consecuencia también son múltiplos 6.
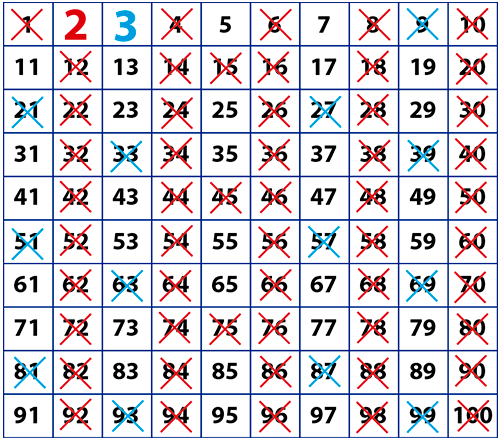
- El siguiente número que no está tachado en el cuadro es el 5. Lo resaltamos con verde como primo y tachamos todos los múltiplos de 5 que no estén tachados aún.
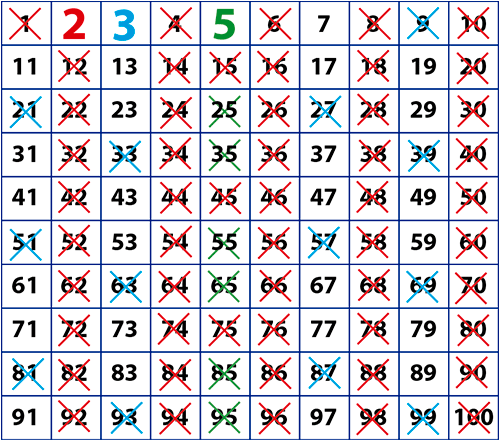
- Ahora corresponde tachar al número 7. Lo resaltamos con morado como primo y tachamos todos los múltiplos de 7 que falten.
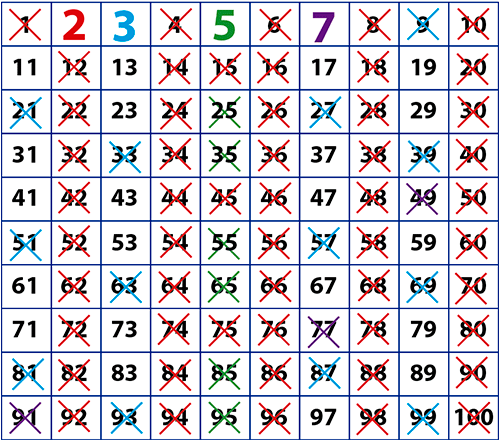
- El proceso realizado se repite hasta que todos los múltiplos de los números primos sean tachados. La criba de Eratóstenes para obtener los primos entre los cien primeros números naturales quedaría como el cuadro que se muestra a continuación. Los números primos están resaltados en rojo, mientras que el uno y los números compuestos han sido tachados.
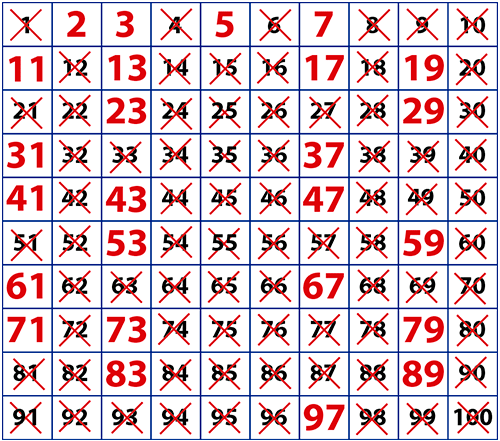
Como se observa en el cuadro en los 100 primeros números naturales hay 25 números primos. Esta es la lista de estos números, ordenada de menor a mayor: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.
¿Quieres hacer tú propia criba de Eratóstenes y demostrar que ya eres un experto en números primos? Te animamos entonces a que descargues y realices las siguientes fichas:
A continuación presentamos una tabla con los números primos entre 1 y 1000:
Números primos hasta el 1000 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 |
| 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 |
| 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 | 421 | 431 | 433 |
| 439 | 443 | 449 | 457 | 461 | 463 | 467 | 479 | 487 | 491 | 499 | 503 |
| 509 | 521 | 523 | 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 | 739 | 743 |
| 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 | 887 | 907 | 911 |
| 919 | 929 | 937 | 941 | 947 | 953 | 967 | 971 | 977 | 983 | 997 | |
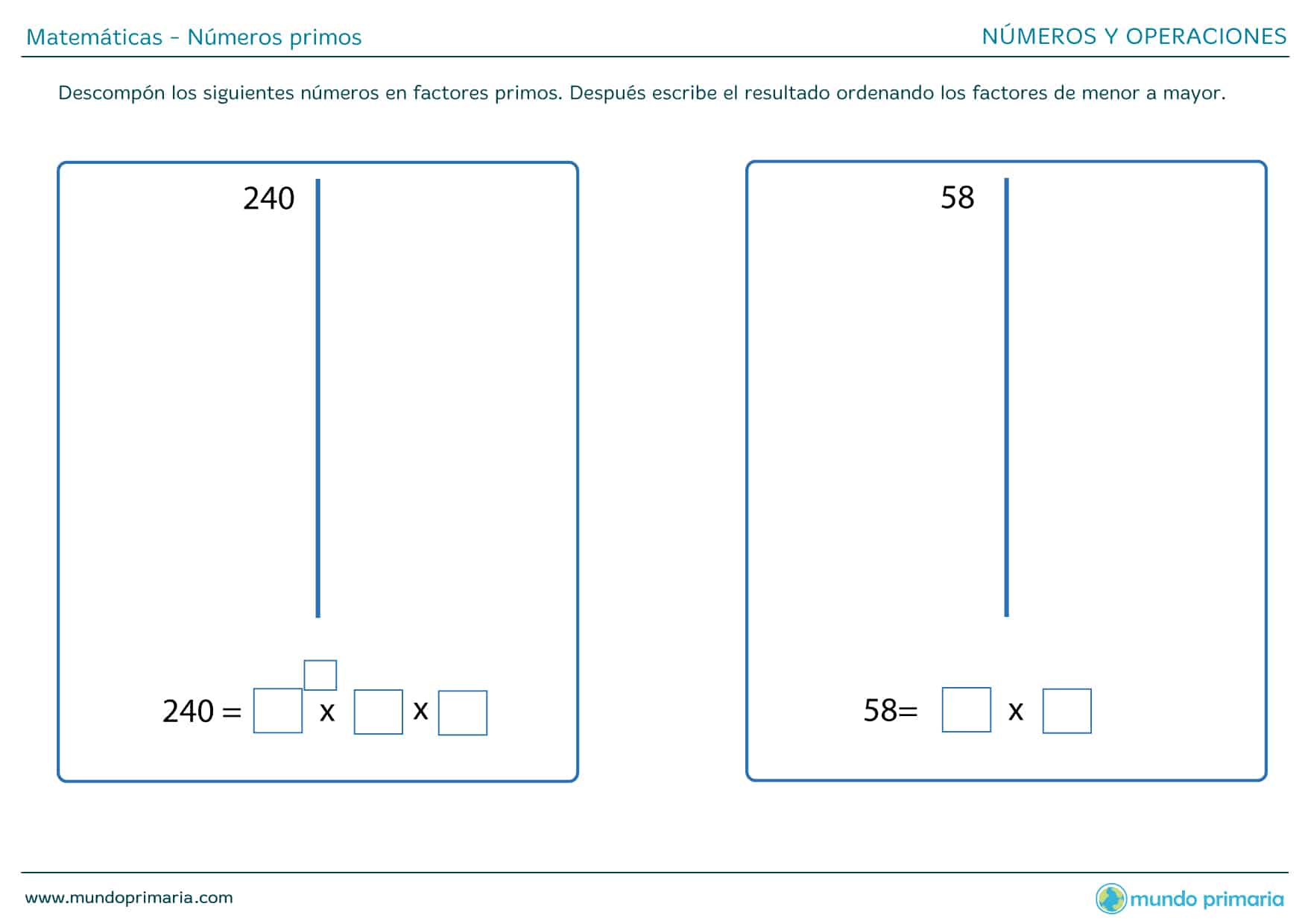
Descomposición de un número primo en factores primos
Al estudiar la multiplicación de números naturales se discutió que el número 18 se puede expresar de diversas maneras, como el producto de dos números. Veamos:
Formas de expresar el número 18 | |
|---|---|
| | 1 x 18 |
 | 2 x 9 |
 | 3 x 6 |
Empleando la propiedad conmutativa de la multiplicación, se tiene que 18 también se puede escribir como 1 x 18, 9x 2 y 6 x 3.
Al observar lo números que multiplicados dan 18 como resultado, se obtiene que alguno de los factores es un número compuesto. ¿Será posible escribir 18 como el producto de factores donde todos sean números primos?
La respuesta es sí.
Veamos:
18 =2 x 9 = 2 x 3 x 3
18 = 3 x 6 = 3 x 2 x 3
Se observa que en cualquiera de los casos que se considere para el 18, éste siempre quedará expresado, de una misma manera, como producto de factores primos.
Es decir, el 18 es el producto de la multiplicación de números primos. Los factores primos de 18 son 2 y 3.
Al aplicar este procedimiento por ejemplo con el 12 tenemos:
12 = 4 x 3 = 2 x 2 x 3
12 = 6 x 2 = 3 x 2 x 2
Es decir, que 12 expresado como la descomposición de factores primos es 2 x 2 x 3.
En el caso del 24 el resultado sería:
24 = 6 x 4
24 = 2 x 2 x 2 x 3
24 = 3 x 2 x 2 x 2
24 =2 x 2 x 2 x 3
Entonces, 24 expresado como la descomposición de su factores primos es 2 x 2 x 2 x 3 = 24
Veamos que ocurre con el número 100. Este número se puede expresar como:
100 = 2 x 50
100 = 4 x 25
100 = 2 x 2 x 25
100 = 2 x 2 x 25
100 = 2 x 2 x 5 x 5
100 = 2 x 2 x 5 x 5
Observa que el número 100 siempre quedará expresado como producto de los factores primos 2 y 5.
El número 100 escrito como la descomposición de sus factores primos es igual a 2 x 2 x 5 x 5.
Otra manera de hacer la descomposición de números compuestos en factores primos es utilizando la idea de divisores. Para saber cómo se hace visualiza los dos vídeos que tienes a continuación donde se explica paso a paso y con ejemplos.
Curiosidades de los números primos
Para finalizar el artículo vamos a comentar algunas curiosidades de los números primos. Algunas pertenecen al mundo de las matemáticas pero otras pueden observarse en el mundo real.
El 2 es el único número primo y par a la vez.

Esto se debe a que todo número par mayor que dos tiene como divisores (al menos) a sí mismo, al número 1 y al 2. Por tanto, todo número par mayor que dos es compuesto.
Los números primos más cercanos son el número 2 y el número 3.

Estos números primos tienen una distancia de solo una unidad. Pero los números primos se hacen cada vez más escasos mientras los números van creciendo y hay mucha más distancia entre ellos.
Algunos insectos viven exactamente 13 o 17 años como larvas.

Este es el caso de las chicharras o cicádidos que viven 13 o 17 años exactamente (los dos números primos) como especie de larvas o parásitos debajo de la tierra, alimentándose de raíces, antes de salir a la superficie tal como las conocemos.
Esto hace que vayan emergiendo por oleadas en vez de que salgan en enjambres completos, y así se preservan de sus depredadores naturales.
Los números primos se usan para «encriptar» o proteger información.

Esto se debe a que al tener un número muy grande, la descomposición de este número en factores primos es muy difícil.
De manera que si se usa un número grande como “candado” para proteger la información, y las “llaves” son los números primos que al multiplicarlos dan como resultado ese número grande, encontrar estos factores primos es muy complicado.
Te dejamos unas actividades para que puedas practicar lo aprendido:
Selecciona un juego 👇 👇 👇

Números primos y compuestos

Números primos y compuestos 2

Múltiplos y divisiones

Númeos primos y compuestos 3

Números primos

Números primos 2

Números primos 3

Números primos 4

Cuestionario

Números primos y compuestos

Números primos y compuestos 2

Múltiplos y divisiones

Númeos primos y compuestos 3

Números primos

Números primos 2

Números primos 3

Números primos 4

Cuestionario
Preguntas frecuentes
¿Qué números son primos del 1 al 100?
Los números primos del 1 al 100 son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.
¿Qué son y cuáles son los números primos?
Un número primo es aquel que tiene exactamente dos divisores distintos: él mismo y el 1. Es decir, solo puede ser dividido exactamente (sin dejar residuo) por 1 y por sí mismo. Los primeros números primos son: 2, 3, 5, 7, 11, 13, 17, y así sucesivamente.
¿Por qué se les llama números primos?
Se les llama números primos porque son los primeros en el sentido de que son los bloques de construcción básicos de los números. Esto es debido a que cada número puede ser descompuesto en un producto de números primos de una manera única (excepto por el orden de los factores).
¿Cuáles son los números primos y compuestos? Ejemplos:
Los números primos, como mencionamos, son aquellos que solo tienen dos divisores: el 1 y ellos mismos. Ejemplos de números primos son 2, 3, 5, 7, 11, etc.
Los números compuestos, por otro lado, son aquellos que tienen más de dos divisores. Por ejemplo, el número 4 es un número compuesto porque tiene tres divisores: 1, 2 y 4. Otros ejemplos de números compuestos son 6, 8, 9, 10, 12, etc.
¿Cómo sabemos si un número es primo?
Para saber si un número es primo, debes intentar dividirlo por todos los números menores que él (excluyendo el 1). Si puedes encontrar algún número que lo divida exactamente (es decir, sin dejar residuo), entonces el número no es primo. Si no puedes encontrar tal número, entonces el número es primo. Sin embargo, para ahorrar tiempo, en realidad solo necesitas probar los divisores hasta la raíz cuadrada del número.
¿Cómo explicar a un niño qué es un número primo?
Podríamos decir que los números primos son como los ingredientes básicos de los números. Son números que solo pueden ser divididos por 1 y por ellos mismos. Imagina que tienes bloques de construcción: los números primos serían los bloques individuales que no puedes dividir en bloques más pequeños.
¿Todos los números primos son impares?
Casi todos los números primos son impares, pero hay una excepción: el número 2. Este es el único número primo que es par. Todos los otros números primos son impares.
¿Por qué el 1 no es un número primo?
El número 1 no se considera un número primo debido a la definición de los números primos. Un número primo es un número que tiene exactamente dos divisores distintos: él mismo y el 1. Sin embargo, el número 1 solo tiene un divisor, que es él mismo (el 1). Por lo tanto, como el número 1 solo tiene un divisor y no dos, no se ajusta a la definición de número primo y por eso no se considera un número primo.
Diferencias entre números primos y compuestos
Los números primos y compuestos son dos categorías diferentes de números enteros. Aquí te dejo algunas diferencias:
Divisores: Los números primos solo tienen dos divisores: 1 y ellos mismos. Por otro lado, los números compuestos tienen más de dos divisores.
Descomposición: Los números compuestos pueden descomponerse en un producto de números primos. Los números primos no pueden descomponerse de esta manera porque solo son divisibles por 1 y por ellos mismos.
Ejemplos: El número 2 es un número primo, ya que sus únicos divisores son 1 y 2. El número 4 es un número compuesto porque tiene tres divisores: 1, 2 y 4.
Recordar que todos los números enteros mayores que 1 son o bien números primos o bien números compuestos. El número 1 es especial y no se clasifica como primo ni como compuesto.
![]() Registrado en SafeCreative.
Registrado en SafeCreative.