Las medidas de masa
En este artículo encontrarás mucha información de valor sobre las medidas de masa y sus unidades. Te invitamos a leerlo para que aprendas cuáles son, cómo se utilizan, de qué manera se hacen las conversiones y a resolver problemas con ellas. Además, verás ejemplos curiosos de monumentos gigantescos y la medida de su masa.
Medidas de masa
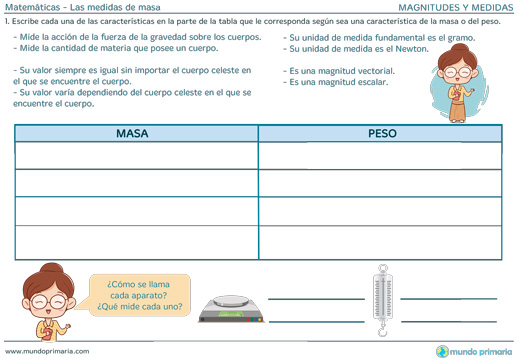
Para medir la cantidad de masa que posee un objeto se utilizan instrumentos como la balanza y la báscula.
- La balanza: Es una palanca de primer grado que posee un punto de apoyo y dos brazos iguales que están a la misma distancia uno del otro. Cuando el objeto al que se le desea medir la masa es colocado en uno de los brazos de la balanza ésta se desequilibra, por lo que es necesario colocar en el otro brazo una cierta cantidad de masa que permita recobrar el balance.

- La báscula: Este instrumento cuenta con una plataforma horizontal, sobre la que se coloca el objeto a pesar. Con este artefacto se mide fácilmente la cantidad de materia de los objetos de gran tamaño.

A partir del gramo se establece el procedimiento de múltiplos y submúltiplos. De esto hablamos en otro apartado de este artículo.
Aquí tienes un vídeo donde puedes comparar elementos según su peso:
Medidas de masa y peso
En la vida cotidiana las personas utilizan las palabras masa y peso como sinónimos, pero la verdad es que existen algunas diferencias entre estos dos términos.
Comencemos definiendo cada uno:
Esto es:
En el planeta Tierra la aceleración tiene un valor constante de 9,8 m/s2 por lo que se puede afirmar que el peso es proporcional a la masa del cuerpo.
El peso es una magnitud vectorial porque está definido por su módulo, dirección y sentido.
Para determinar el peso de un objeto se utiliza el dinamómetro o la balanza de resorte.

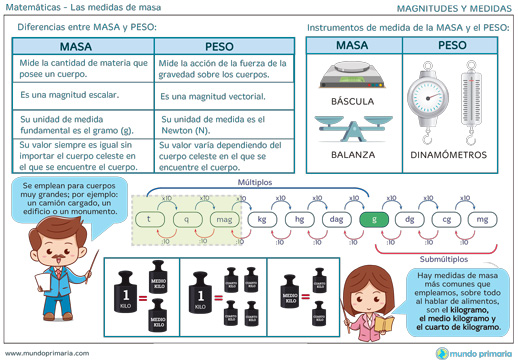
Diferencias entre la masa y el peso
Como ya has podido notar los conceptos de masa y peso tienen diferencias importantes.
Aunque estas diferencias son ampliamente aceptadas en el mundo de las ciencias, la verdad es que en la vida cotidiana la personas hablan del peso cuando lo que realmente están midiendo es la masa de un cuerpo.
Por ejemplo, en la frutería las personas hablan de pesar las frutas o los vegetales cuando realmente lo que están determinando es la cantidad de materia de los alimentos que desean llevar.
A continuación te presentamos una tabla con las diferencias que existen entre la masa y el peso.
| Masa (m) | Peso (p) |
| Unidad de medida: kilogramo, gramo, miligramo. | Unidad de medida: Newton (N). |
| Se mide con la balanza o la báscula. | Se mide con el dinamómetro o la balanza de resorte. |
| Es una magnitud escalar. | Es una magnitud vectorial. |
| Cantidad de materia que posee un cuerpo | Acción que ejerce la fuerza de gravedad |
| Su valor siempre es igual sin importar el cuerpo celeste en el que se encuentre el cuerpo. | Su valor varía dependiendo del cuerpo celeste en el que se encuentre el objeto. |
Con esta ficha podrás trabajar con los conceptos de masa y peso.
Ejemplos de medidas de masa
En la vida diaria usamos las medidas de masa en actividades como cocinar, ir al mercado, cuando vamos al doctor, entre otros.
Algunas de las medidas de masa más comunes que empleamos, especialmente cuando hablamos de alimentos son el kilogramo, el medio kilogramo y el cuarto de kilogramo.
Veamos gráficamente, usando un kilogramo de harina, las equivalencias entre estas tres medidas:

Un kilogramo es equivalente a dos medios kilogramos.

Un kilogramo es equivalente a cuatro cuartos de kilogramo.

Medio kilogramo es equivalente a dos cuartos de kilogramo.
Como dijimos anteriormente, medimos la cantidad de materia que hay en los alimentos, nuestro equipaje o el cuerpo humano, pero te has preguntado cuál es la cantidad de masa que hay en cuerpos como la Estatua de la Libertad, el Planeta Tierra, el Taj Mahal y El Cristo Redentor de Brasil.
A continuación te decimos cuánta materia tienen estos ejemplos:


Tabla de medidas de masa
El gramo tiene múltiplos y submúltiplos. Los múltiplos del gramo son unidades de medida más grandes que el gramo, y se llaman decagramo (dag), hectogramo (cg), kilogramo (kg) y miriagramo (mag).
Los submúltiplos del gramo, por su parte, son más pequeños que el gramo, y se llaman decigramo (dg), centigramo (cg) y miligramo (mg).
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
Veamos ahora las equivalencias entre estas unidades:
| 1 gramo equivale a | 10 decigramos (dg) |
| 100 centigramos (cg) | |
| 1.000 miligramos (mg) | |
| 0,1 decagramos (dag) | |
| 0,01 hectogramos (hg) | |
| 0,001 kilogramos (kg) | |
| 0,0001 miriagramos (mag) |
Haremos especial mención a dos unidades de medida que se usan frecuentemente, y son el quintal (q) y la tonelada métrica (Tm), conocida generalmente como Tonelada.
| 1 q = 100 kg |
| 1 Tm = 1.000 kg |
El quintal se usa en los mercados internacionales para comercializar productos como el café, mientras que la Tonelada métrica (tonelada) se usa para comercializar otra gran variedad de productos como alimentos y distintos tipos de materia prima.
Emplea la siguiente ficha para valorar si manejas con fluidez las unidades de medida de la masa.
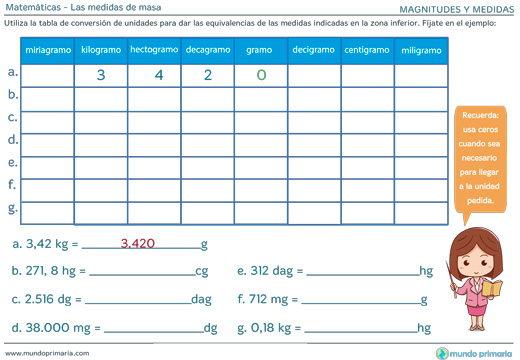
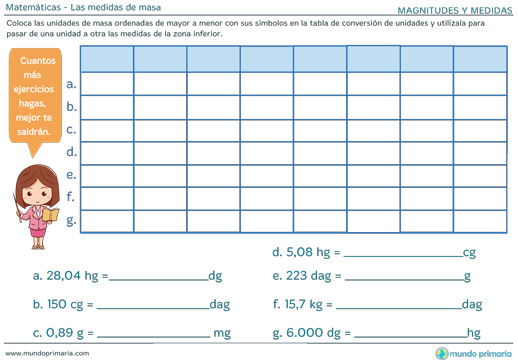
Conversión de medidas de masa
Como has notado las equivalencias entre los múltiplos y submúltiplos del gramo se corresponden con la forma en que funciona el Sistema de Numeración Decimal. Esto significa que 1 unidad mayor equivale a 10 veces la unidad anterior.
Nuestro Sistema de Numeración Decimal (SND) es posicional y base 10. Es decir, 10 unidades de cualquier orden equivalen a 1 unidad del orden inmediatamente superior. Y viceversa, una unidad mayor equivale a 10 veces la unidad inmediatamente anterior.
Observa este ejemplo:
- 30 unidades forman 3 decenas
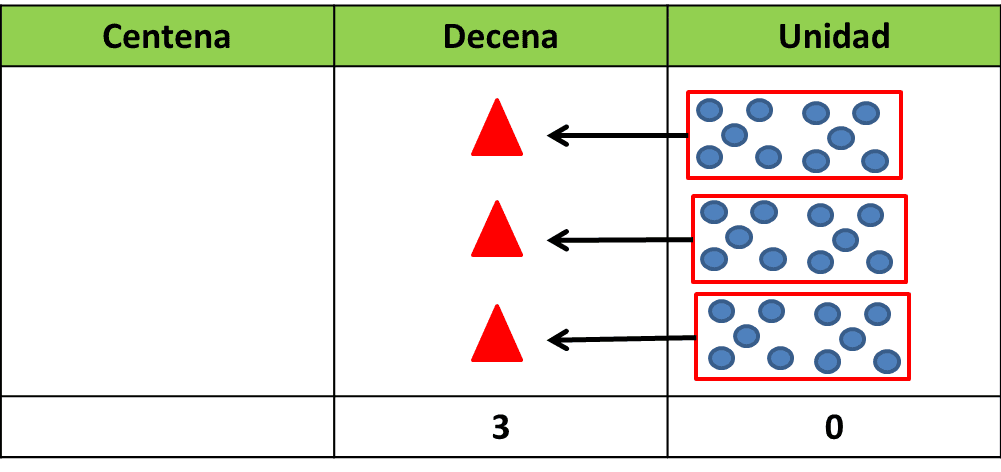
En la imagen observamos como 30 unidades forman 3 decenas. Agrupamos las unidades en 3 grupos de 10, y cada uno de estos grupos forma una decena, completando así las 3 decenas.
- 24 decenas forman dos centenas y cuarenta unidades (o 240 unidades)
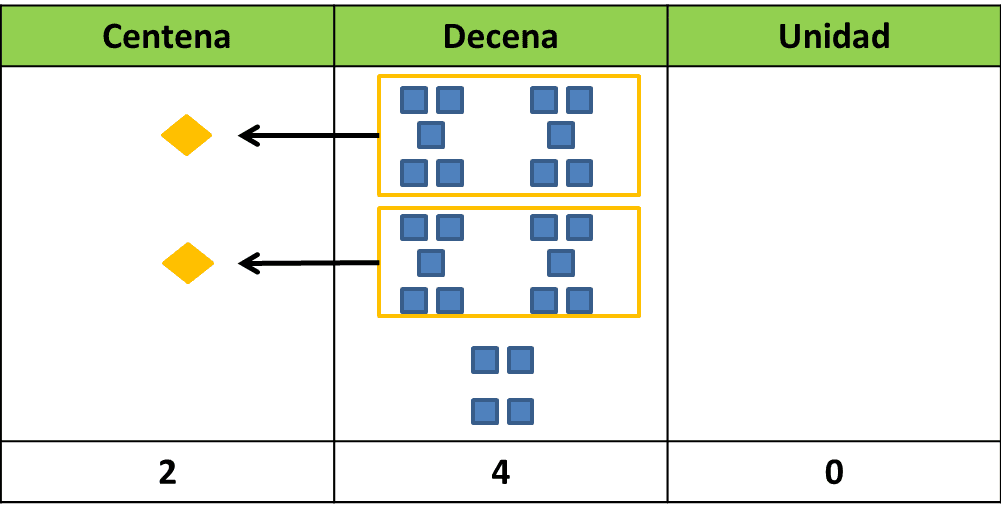
La gráfica explica cómo las 24 decenas forman dos grupos de 10, que equivalen a 2 centenas, y quedan 4 decenas, que equivalen a 40 unidades.
Ahora bien, el sistema de numeración decimal y el sistema de unidades de medida de masa funcionan de forma similar.
Veamos, por ejemplo, las equivalencias de 5 gramos, para ello usaremos la tabla que construimos en el apartado anterior, empezando con los submúltiplos.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 5 | |||||||
| 5 | 0 | ||||||
| 5 | 0 | 0 | |||||
| 5 | 0 | 0 | 0 |
5 gramos equivalen a 50 decigramos, 500 centigramos y 5.000 miligramos.
| 5 g | 5.000 mg |
| 500 cg | |
| 50 dg |
Determinaremos la equivalencia de estos mismos 5 gramos con los múltiplos del gramo, usemos la tabla para ello.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 5 | |||||||
| 0 | 5 | ||||||
| 0 | 0 | 5 | |||||
| 0 | 0 | 0 | 5 | ||||
| 0 | 0 | 0 | 0 | 5 |
5 gramos equivalen a 0,5 dag, 0,05 hg, 0,005 kg y 0,0005 mag.
| 5 g | 0,5 dag |
| 0,05 hg | |
| 0,005 kg | |
| 0,0005 mag |
Vamos a ver un par de ejemplos de conversión de medidas de masa:
- Ejemplo 1: ¿A cuántos hectogramos equivalen 2300 centigramos?
- Lo primero que haremos es escribir 2300 centigramos en la tabla de equivalencias.
- Esto lo haremos de izquierda a derecha, empezando con el 0 en el lugar de los centigramos, después el otro 0 en el lugar de los decigramos, continuamos con la cifra 3 en el lugar de los gramos, y el 2 en el lugar de los decagramos.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 2 | 3 | 0 | 0 |
- De esta forma tenemos escrito en la tabla los 2300 centigramos.
- Luego, como queremos saber su equivalencia en hectogramos, completamos con ceros hasta llegar a hectogramos. Nos queda así:
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 0 | 2 | 3 | 0 | 0 |
- En este caso, cero es la parte entera del número que nos ha resultado, y los otros números son la parte decimal. Para leerlo correctamente colocaremos una coma.
- Nos queda entonces que 2300 centigramos equivalen a 0,23 hectogramos.
- En este caso, cero es la parte entera del número que nos ha resultado, y los otros números son la parte decimal. Para leerlo correctamente colocaremos una coma.
- Ejemplo 2: ¿A cuántos gramos equivalen 3,6 kilogramos?
- Empezamos escribiendo el número 3,6 kg en la tabla de equivalencias. Nos queda así:
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 3 | 6 | 0 | 0 |
- Hemos completado con ceros la cantidad en la tabla hasta llegar a la casilla del gramo (g), que es la unidad a la que queremos transformar los kilogramos (kg).
- Recordemos que 3,6 kg es igual a 3 kg + 6 hg. Por eso escribimos el 6 en la casilla de los hectogramos.
En este apartado aprendiste a hacer conversiones entre las unidades de masa, utilizando los principios del Sistema de Numeración Decimal y la tabla de equivalencias.
Ejercicios de medidas de masa
A continuación te dejamos la resolución paso a paso de ejercicios de medidas de masa. Para ello vamos a utilizar lo que aprendimos en el apartado anterior acerca de la tabla de equivalencias y la conversión de medidas de masa.
Convertir las medidas de masa a las que se indican:
- 38 cg a hg
- Empezamos escribiendo la cantidad que nos dan inicialmente, que en este caso es 38 cg, en la tabla de equivalencias.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 0 | 0 | 0 | 3 | 8 |
- Luego, nos fijamos en la casilla de la unidad de masa a la que queremos transformar esta cantidad, en este ejemplo son los hectogramos, para completar con ceros.
- Para leer el número correctamente agregamos un coma luego de la unidad de los hectogramos.
- Tenemos como resultado que 38 cg son equivalentes a 0,0038 hectogramos.
- 520 dag a kg
- Lo primero que haremos es escribir el número de decagramos en la tabla (520 dag).
- Luego nos fijamos en la casilla de la unidad de medida a la que queremos convertirlos, que en este caso son los kilogramos.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 5 | 2 | 0 |
- En este caso no es necesario completar con ceros. Podemos agregar la coma luego del 5, que representa la unidad de los kilogramos, para leer el número correctamente.
- Nos queda entonces que 520 dag es equivalente a 5,2 kg.
- En este caso no es necesario completar con ceros. Podemos agregar la coma luego del 5, que representa la unidad de los kilogramos, para leer el número correctamente.
- 15 hg a cg
- Vamos ahora a convertir 15 hg a cg por lo que vamos a representar este número de hectogramos en la tabla.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 1 | 5 | 0 | 0 | 0 | 0 |
- Completamos con ceros hasta llegar a la unidad centigramos, que es la unidad a la que queremos convertir la cantidad de hectogramos que nos dan.
- Entonces nos queda que 15 hg es igual a 150.000 cg.
- Completamos con ceros hasta llegar a la unidad centigramos, que es la unidad a la que queremos convertir la cantidad de hectogramos que nos dan.
- 35 g a mg
- En este caso pasaremos 35 gramos a miligramos. Comenzamos escribiendo los 35 g en la tabla de equivalencias.
- Recuerda que lo hacemos de derecha a izquierda escribiendo primero 5 en la unidad del gramo y luego el 3 en los hectogramos (porque 30 g es igual a 3 hg).
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 3 | 5 | 0 | 0 | 0 |
- Después completamos con ceros hasta llegar a los miligramos, al hacerlo nos queda lo siguiente:
- 35 g es equivalente a 35.000 mg.
- Después completamos con ceros hasta llegar a los miligramos, al hacerlo nos queda lo siguiente:
- 1,5 g a kg
- Transformaremos 1,5 gramos a kilogramos. Primero escribimos el número de gramos en la tabla. Luego completamos con ceros hasta llegar a los kilogramos.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 0 | 0 | 0 | 1 | 5 |
- Para leer el número correctamente debemos colocar una coma luego de la unidad kilogramo.
- Por último, nos queda que 1,5 gramos es igual a 0,0015 kg.
- Para leer el número correctamente debemos colocar una coma luego de la unidad kilogramo.
Antes de hacer unos cuantos problemas, te dejamos unas fichas para que hagas conversiones de unidades.
Problemas de conversión de medidas de masa
Vamos a resolver paso a paso algunos problemas con medidas de masa.
- ¿Cuál de las siguientes cajas pesa más?

- Para resolver este problema vamos a representar en la tabla de conversiones la cantidad escrita en cada caja.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 8 | 5 | 0 | 0 | 0 | |||
| 3 | 5 | 0 | 0 | ||||
| 9 | 0 | 0 | 0 |
- Vamos a llevar todas las cantidades a miligramos. Para ello completamos con ceros.
- Como puedes observar, la caja que pesa más es la de 85 g, que es equivalente a 85.000 mg.
- Tengo en el frutero de mi casa 0,8 kg de manzana, 450 g de peras y un cuarto de kilogramo de mango. ¿Cuántos kilogramos de fruta tengo en total en mi frutero?
- Para resolver este problema debemos totalizar la cantidad de fruta que hay, pero debemos dar la respuesta en kilogramos.
- Por ello, empezaremos llevando a kilogramos la cantidad que hay de cada fruta.
- Como puedes ver la manzana ya está expresada en kilogramos, y tenemos un número para la cantidad de kilogramos. De manera que trabajaremos con las peras y el mango.
- Transformaremos primero los 450 g de peras en kilogramos.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 0 | 4 | 5 | 0 |
- Al completar con ceros y colocar la coma en el lugar de la unidad kilogramos tenemos que:
- 450 g de peras son equivalentes a 0,45 kg
- Ahora vamos con los mangos. Tenemos un cuarto de kilogramo de mangos.
- Recordemos que un cuarto de kilogramos de mango equivale a 250 g de mango. Llevemos esta cantidad a kilogramos. Para hacerlo, escribimos la cantidad en gramos en la tabla y completamos con ceros hasta llegar a kilogramos.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 0 | 2 | 5 | 0 |
- Tenemos que un cuarto de kilogramo de mangos es equivalente a 0,25 kilogramos.
- Por último realizamos la adición correspondiente:
- 0,8 kg de manzanas + 0,45 kg de peras + 0,25 kg de mangos = 1,50 kg
- En mi frutero tengo 1,5 kg de frutas. También podemos decir que hay un kilogramo y medio de frutas en el frutero.
- Lee la siguiente información:
- El cerebro de un humano adulto tiene una masa de aproximadamente 1,4 kilogramos.
- ¿Qué significado tienen las 4 décimas de kg en la información? Explica por qué no se da un dato exacto.
- Para responder a la interrogante que se nos presenta vamos a representar la medida 1,4 kg en la tabla de equivalencias. Veamos:
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 1 | 4 | 0 | 0 |
- Recuerda que 1,4 kg es igual a 1 kg + 0,4 kg. Es por ello, que hemos escrito 1 en la casilla de los kilogramos y 4 en la de los hectogramos ( 0,4 kilogramos se puede entender como 4 de los 10 hectogramos que necesitamos para formar un kilogramo).
- A partir de la tabla de equivalencias se puede afirmar que:
- 1 kilogramo equivale a 1.000 gramos.
- 0,4 kilogramos equivalen a 400 gramos.
- Partiendo de las equivalencias anteriores tenemos que:
1 kg + 0,4 kg = 1.000 g + 400 g = 1.400 g
- Por esta razón 4 décimas de kg equivalen a 400 gramos que es una parte de la masa de un cerebro adulto. Este órgano pesa aproximadamente 1.400 gramos o 1,4 kg.
- No se acostumbra a dar una medida exacta de la cantidad de masa de un cerebro adulto porque ésta varía dependiendo del sexo y de la época en la que se hizo la medición.
- María tiene dos perritos: Pelusa es de color marrón y pesa 1.930 decagramos. El otro perro, Azúcar, es negro y pesa 28 kilogramos. ¿Cuál de los dos gatos es el más pesado? ¿Cuál es la diferencia de masa que hay entre los dos gatos?

- Lo primero que haremos será representar ambas medidas en la tabla de equivalencias.
- Pelusa: 1930 dag
- Azúcar: 28 kg
- Es importante tener en cuenta que para escribir 1.930 decagramos en la tabla de equivalencias, debemos ubicarnos en los decagramos y comenzar a escribir el número de derecha a izquierda.
- Es decir, colocamos la cifra 0 en el lugar de los decagramos, la siguiente cifra que es 3 la colocamos en los hectogramos, el nueve lo escribimos en el lugar de los kilogramos y el uno lo copiamos en los miriagramos.
- De esta manera se escribe 1.930 decagramos en la tabla de equivalencias.
- Para representar el peso de Azúcar en la tabla de equivalencias realizamos un proceso similar al anterior. Es decir, escribimos el 8 en la casilla de los kilogramos y 2 en los miriagramos. Finalizamos colocando un cero en el lugar de los hectogramos y otro cero en la casilla de los decagramos.
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 1 | 9 | 3 | 0 | ||||
| 2 | 8 | 0 | 0 |
- En la tabla se observa que el peso de Pelusa es 1.930 dag y el de Azúcar 2.800 dag.
- Entonces, el perro más pesado es Azúcar y la diferencia de peso entre ambos es 2.800 dag – 1930 dag = 870 dag.
- El ascensor de carga de un centro comercial resiste un peso de 1.800 kg y quiero trasladar en este elevador paquetes que pesan 900 gramos cada uno. ¿Cuántos paquetes puedo colocar como máximo sin superar el peso?

- Vamos a representar los 900 gramos en la tabla de equivalencias para saber cuántos kilogramos son. Veamos:
| mag | kg | hg | dag | Gramo (g) | dg | cg | mg |
| 0 | 9 | 0 | 0 |
- De la tabla de equivalencias se obtiene que 900 gramos equivalen a 0,9 kg.
- Como queremos saber cuántos paquetes de 0,9 kg (900 gramos) caben en 1.800 kg, procedemos a dividir 1.800 kg entre 0,9 kg. Resultando lo siguiente:
- 1.800 0,9 es equivalente a 18.000 ÷ 9.
- Al realizar la división 18.000 ÷ 9 se obtiene como cociente 2.000.
- Entonces, en el ascensor se pueden colocar, como máximo, 2.000 paquetes de 900 gramos cada uno sin que se supere el peso establecido.
No podíamos concluir el texto sin ofrecerte unas cuantas actividades para que halles las soluciones gracias a las unidades de medida de masa. Además, en la ficha de apuntes que puedes descargar tienes la información del texto resumida.
Selecciona un juego 👇 👇 👇

Medidas de masa - 1

Medidas de masa - 2

Medidas de masa - 3

Medidas de masa - 4

Medidas de masa - 5

Medidas de masa - 6

Medidas de masa - 7

Medidas de masa - 8

Cuestionario

Medidas de masa - 1

Medidas de masa - 2

Medidas de masa - 3

Medidas de masa - 4

Medidas de masa - 5

Medidas de masa - 6

Medidas de masa - 7

Medidas de masa - 8

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.