Los números son uno de los elementos más importantes de la matemática, muchas personas, inclusive matemáticos de prestigio, se han dedicado al estudio de estos apasionantes signos que expresan cantidades. Por ello, ideas como las de divisores y Máximo Común Divisor han captado la atención de chicos y jóvenes desde hace mucho tiempo.
En este artículo aprenderás qué es el Máximo Común Divisor, conocerás cómo aplicar su algoritmo, verás ejercicios y problemas resueltos paso a paso que te ayudarán a comprender qué significa que un número sea el mayor de los divisores comunes.
No dejes de leer este artículo en el que encontrarás ejercicios y problemas que te permitirán comprender la idea de Máximo Común Divisor.
¿Qué es el máximo común divisor?
El Máximo Común Divisor es el mayor de los divisores comunes.
Veamos un ejemplo con 8, 12 y 20 para entender qué significa que un número sea el mayor de los divisores comunes.
Lo primero que haremos será determinar los divisores de 8, 12 y 20.
Los divisores de 8 son: 1, 2, 4, 8.
Los divisores de 12 son: 1, 2, 3, 4, 6, 12.
Los divisores de 20 son: 1, 2, 4, 5, 10, 20.
RECUERDA QUE:
● 4 es divisor de 8, porque al dividir 8 entre 4, el residuo de esta división es igual a cero. Dicho de otra manera 4 divide a 8, porque 8 = 4 x 2, siendo 2 el cociente de la división
● 3 es divisor de 12, porque al dividir 12 entre 3 obtenemos como residuo cero, es decir, la división es exacta y se puede escribir como sigue 12 = 3 x 4. El número 4 es el cociente de esta división.
● 2 es divisor de 20, porque al dividir 20 : 2, el resto de esta división es igual a cero. Lo que permite escribir que 20 = 2 x 10, siendo el número 10 el cociente de la división.
Ahora veamos cuáles son los divisores comunes de 8, 12 y 20
NO OLVIDES QUE:
Los divisores de 8 son: 1, 2, 4, 8.
Los divisores de 12 son: 1, 2, 3, 4, 6, 12.
Los divisores de 20 son: 1, 2, 4, 5, 10, 20.
Los divisores comunes de 8, 12 y 20 son: 1, 2, 4.
Sólo nos falta escoger el mayor de los divisores comunes. Es decir, el mayor número entre 1, 2 y 4. En este caso es 4.
Concluimos, que el mayor de los divisores comunes de 8, 12 y 20 es 4
El número 4 es el mayor de los divisores comunes de 8, 12 y 20.
Es decir, el Máximo Común Divisor de 8, 12 y 20 es 4.
Cuando los números son pequeños podemos utilizar el método que acabamos de ver para calcular el Máximo Común Divisor de dos o más números.
Por ejemplo, calcular el Máximo Común Divisor de 5, 15 y 25 mediante el método que acabamos de ver es muy sencillo. Veamos:
Primero calculamos los divisores de 5, 15 y 25
Los divisores de 5son: 1, 5.
Los divisores de 15 son: 1, 3, 5, 15.
Los divisores de 25 son: 1, 5, 25.
1 y 5 son los divisores comunes de 5, 15y 25. El mayor entre estos dos divisores es el 5. Entonces, el mayor de los divisores comunes es el 5. Es decir:
El Máximo Común Divisor (MCD) de 5, 15,25 = 5
Pero si los números son grandes, por ejemplo 81, 54y 108, este método es poco efectivo. Por esta razón existe un algoritmo que nos permite calcular el Máximo Común Divisor de forma rápida y efectiva.
¿Cómo sacar el máximo común divisor?
El procedimiento para calcular el Máximo Común Divisor (MCD) de dos o más números es bastante sencillo, lo único que necesitas es prestar mucha atención a cada uno de los pasos que te explicamos a continuación para que logres ser un experto en este tema.
Paso 1:Descompón los números en sus factores primos.
Si quieres calcular el Máximo Común Divisor de 18, 21 y 24, entonces descompón cada uno de estos números en sus factores primos. Veamos:
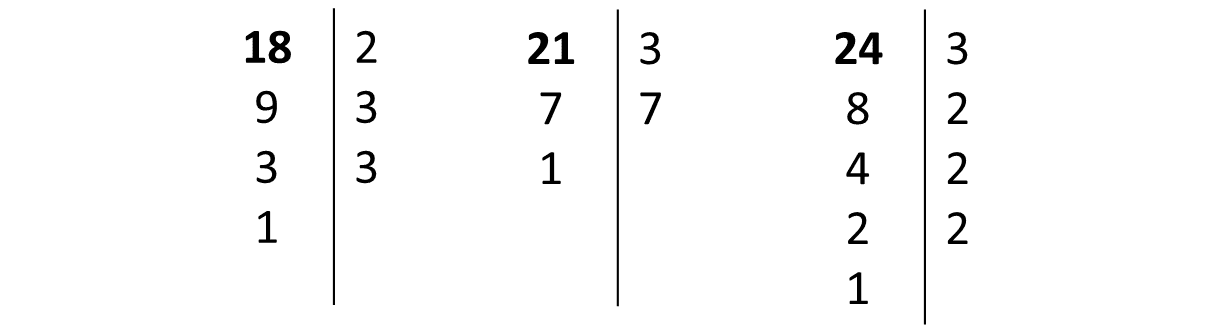
18 = 2 x 3 x 3 = 2 x 3²
21 = 3 x 7
24 = 3 x 2 x 2 x 2 = 3 x 2³
Paso 2: Selecciona el o los factores que son comunes en las tres descomposiciones.
18 = 2 x 3 x 3 = 2 x 3²
21 = 3 x 7
24 = 3 x 2 x 2 x 2 = 3 x 2³
El factor que es común en las tres descomposiciones es el 3
Paso 3: Escogemos el factor común, en este caso es 3, con el menor exponente.
18 = 2 x 3 x 3 = 2 x 3²
21 = 3 x 7
24 = 3 x 2 x 2 x 2 = 3 x 2³
El factor común con el menor exponente es el 3
Concluimos que:
El Máximo Común Divisor de 18, 21 y 24 es 3.
También se puede escribir:
MCD (18, 21, 24) = 3
Veamos un ejemplo más:Calculemos el MCD (54, 81, 108).
Descomponemos los números 54, 81 y 108 en factores primos.
Luego, identificamos el factor o los factores que son comunes en las tres descomposiciones.
54 = 2 x 3 x 3 x 3
162 = 2 x 3 x 3 x 3 x 3
108 = 2 x 2 x 3 x 3
= 2 x 3³
= 2 x 34
= 2² x 3³
En este caso los factores comunes son 2 y 3.
Por último, seleccionamos los factores comunes con el menor exponente.
54 = 2 x 3 x 3 x 3
162 = 2 x 3 x 3 x 3 x 3
108 = 2 x 2 x 3 x 3
= 2 x 3³
= 2 x 34
= 2² x 3³
Los factores comunes con el menor exponente son 2 x 3³
Entonces:
MCD (54, 108, 162) = 2 x 3³ = 2 x 3 x 3 x 3 = 54
Un caso especial del Máximo Común Divisor
Cuando los números son todos primos, entonces el Máximo Común Divisor de esos números es igual a 1.
Por ejemplo: Calculemos el MCD (5, 7, 11).
Como 5, 7 y 11 son números primos su descomposición en factores primos es:
5 = 5 x 1
7 = 7 x 1
11 = 11 x 1
El único factor común en las tres descomposiciones es el 1. Por esta razón:
El MCD (5, 7, 11) = 1
Veamos otros ejemplos:
MCD (13, 17, 23) = 1
13, 17 y 23 son números primos por lo que su Máximo Común Divisor es 1
MCD (5, 17, 29) = 1
En este ejemplo el Máximo Común Divisor también es 1, porque 5, 17 y 29 son números primos.
MCD (2, 3, 5) = 1
2, 3 y 5 son números primos por esta razón su Máximo Común Divisor es 1.
El Máximo Común Divisor de dos o más números primos es siempre igual a 1
Ejemplos usando el MCD
Veamos algunos ejemplos de cómo calcular el máximo común divisor de dos o más números.
Ejemplo 1: ¿Cuál es el máximo común divisor de 20 y 64?
Paso 1: Descomponemos ambos números en factores primos
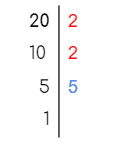20= 2 x 2 x 5
64 = 2 x 2 x 2 x 2 x 2
= 2² x 5
= 25
Paso 2: Buscamos los factores comunes con su menor exponente.
En este caso el único factor común es el 2, y el que tiene el menor exponente es 2²
Paso 3: Calculamos el Máximo Común Divisor de los números dados.
MCD (20,64) = 22 = 2 x 2 = 4
Ejemplo 2: Hallar el MCD de 45, 60 y 30.
Paso 1: Descomponemos ambos números en factores primos
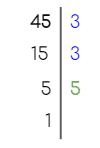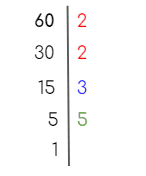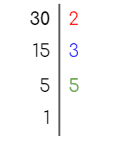45= 3 x 3 x 5
60 =2 x 2 x 3 x 5
30 = 2 x 3 x 5
= 3² x 5
= 2² x 3 x 5
Paso 2: Buscamos los factores comunes con su menor exponente.
En este caso los factores comunes con su menor exponente son el 3 y el 5.
Paso 3: Calculamos el Máximo Común Divisor de los números dados.
MCD (45,60,30) = 3 x 5 = 15
Ejemplo 3: Calcula el Máximo Común Divisor de 80 y 140.
Paso 1: Descomponemos ambos números en factores primos.
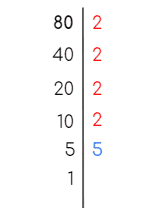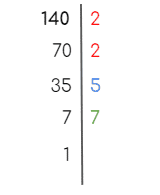80= 2 x 2 x 2 x 2 x 5
140 = 2 x 2 x 5 x 7
= 24 x 5
= 2² x 5 x 7
Paso 2: Buscamos los factores comunes con su menor exponente.
En este caso los factores comunes con su menor exponente son 22 y 5.
Paso 3: Calculamos el Máximo Común Divisor de los números dados.
MCD (45,60,30) = 22 x 5 = 4 x 5 = 20
Con estas fichas podrás practicar los pasos para hallar el máximo común divisor como se ha visto en los ejemplos anteriores.
¿Cómo resolver problemas con el máximo común divisor?
En esta sección encontrarás problemas que se resuelven usando lo que has aprendido acerca del Máximo Común Divisor (MCD). Verás el paso a paso para que aprendas cómo resolver problemas con MCD.
Problema 1
Patty quiere hacer lazos para decorar en Navidad. Para ello tiene dos cintas rojas del mismo grosor pero de diferente largo, una mide 90 cm y otra mide 54 cm.
Si Patty quiere que todos los lazos se hagan con trozos de cinta de igual longitud, y lo más largos posibles, ¿cuántos trozos debe cortar de cada cinta? ¿cuánto debe medir cada trozo con el que hará los lazos?
Respuesta:
Lo primero que debemos hacer es determinar cuáles son los divisores comunes de 90 y 54, para asegurar que cada trozo que cortamos quede de igual longitud.
Los divisores de 90 y 54 son los siguientes:
Divisores de 90
Divisores de 54
1, 3, 5, 9 y 10.
1, 3, 6 y 9.
Hemos resaltado los divisores comunes de 54 y 90, que son 1, 3 y 9.
Ahora veamos cuál es el máximo común divisor.
Podemos ver que el mayor de los divisores comunes es 9. Por lo que 9 es el Máximo Común Divisor de 90 y 54.
Esto quiere decir que podemos hacer trozos de 9 cm con cada pedazo de cinta. Los trozos nos quedarán del mismo tamaño y no sobrará nada. Observa:
Además, al ser 9 el Máximo Común Divisor de ambos números, nos aseguramos de que los trozos de 9 cm son los más largos que podemos hacer.
Ahora podemos responder las preguntas que nos hicieron en el problema:
¿Cuántos trozos debe cortar de cada cinta?
Debe cortar 10 trozos de la cinta que mide 90 cm y 6 trozos de la cinta que mide 54 cm.
¿Cuánto debe medir cada trozo con el que hará los lazos?
Cada trozo debe medir 9 cm.
Problema 2
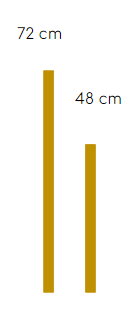
Simón necesita hacer un trabajo con trozos de listones que tengan igual longitud. Además quiere que sean lo más largos posible, y que no le sobre ningún pedazo para aprovechar mejor la madera. Si Simón tiene que cortar los pedazos de un listón que miden 72 cm y de otro listón de 48 cm, ¿cuánto debe medir cada trozo de listón?, y ¿cuántos trozos obtendrá de cada listón?
Respuesta:
Como en el problema 1, debemos encontrar el Máximo Común Divisor de 72 y 48.
Recuerda que esto nos ayuda a saber cuál es el tamaño en centímetros del trozo más largo que podemos cortar de cada listón, sin que sobre nada.
Descomponemos estos números en factores primos:
72= 2³ x 3²
64 = 24 x 3
Tomamos los factores comunes con su menor exponente: 23 y 3. Entonces,
MCD (72,48) = 23 x 3 = 8 x 3 = 24
Esto significa que la longitud mayor de los trozos en los que podemos dividir los listones es de 24 cm.
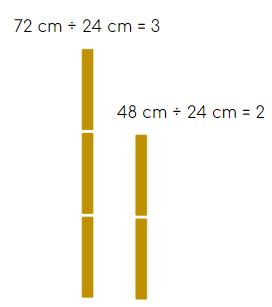
Ahora vamos a responder las preguntas que nos hacen en el problema.
¿Cuánto debe medir cada trozo de listón?
Cada trozo de listón debe medir 24 cm.
¿Cuántos trozos obtendrá de cada listón?
Del listón que mide 72 cm obtendrá 3 trozos y tendrá 2 trozos del listón que mide 48 cm.
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇
Máximo Común Divisor 1
Máximo Común Divisor 2
Máximo Común Divisor 3
Máximo Común Divisor 4
Cuestionario
Registrado en SafeCreative.
Mª Gabriela Gracia y Darwin Silva
Profesores universitarios. Magísters en Educación Mención Enseñanza de la Matemática. Investigadores en el área de innovaciones educativas.
Registrado en SafeCreative.