Jerarquía de las operaciones
Conocer acerca de la jerarquía de las operaciones te permite realizar operaciones combinadas de suma, resta, multiplicación y división (e incluso de potencias y raíces) con la certeza de empezar por donde debes hacerlo. Esto te ayudará a obtener el resultado correcto y a resolver problemas de matemática con mayor facilidad.
En este artículo aprenderás todo lo que necesitas saber sobre la jerarquía de las operaciones.

Qué es la jerarquía de operaciones
Por ejemplo, observa la siguiente expresión:
Como ves, en esta expresión están combinadas las operaciones básicas de la aritmética, que son la adición o suma, sustracción o resta, multiplicación y división.
Si no sabes por dónde empezar puedes obtener un resultado completamente distinto al esperado.
Presta atención al siguiente ejemplo de cómo resolver una expresión con la jerarquía de operaciones y sin la jerarquía de operaciones:
| Sin la jerarquía de las operaciones | Usando la jerarquía de las operaciones |
| 6 + 3 + 4 x 9 – 12 ÷ 3 | 6 + 3 + 4 x 9 – 12 ÷ 3 |
| 6 + 3 + 4 x 9 – 12 ÷ 3 | 6 + 3 + 4 x 9 – 12 ÷ 3 |
| 9 + 4 x 9 – 12 ÷ 3 | 6 + 3 + 36 – 12 ÷ 3 |
| 13 x 9 – 12 ÷ 3 | 6 + 3 + 36 – 4 |
| 117 – 12 ÷ 3 | 9 + 36 – 4 |
| 105 ÷ 3 | 45 – 4 |
| =35 | =41 |
| ¡INCORRECTO! | ¡CORRECTO! |
Como puedes darte cuenta, es necesario usar la jerarquía de las operaciones para obtener el resultado correcto de las operaciones. Ahora veamos en qué consisten estas reglas de la jerarquía de las operaciones para que puedas seguirlas.
Cuáles son las reglas de la jerarquía de operaciones básicas
Al resolver operaciones matemáticas es muy importante que hagas las operaciones en el orden correcto, de acuerdo a la jerarquía que tienen. Si no lo haces es posible que termines con una respuesta errónea.
La idea básica de la jerarquía de las operaciones es que hagas algunas operaciones, como la multiplicación, antes que otras, como la suma.
Estas son las reglas de la jerarquía de operaciones:
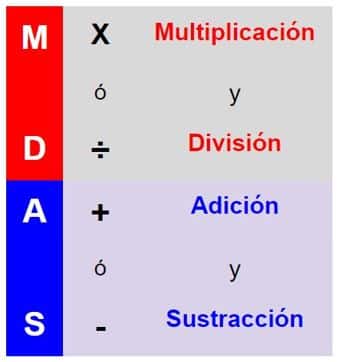
- Resuelve primero las multiplicaciones y las divisiones.
- Luego resuelves las adiciones (sumas) o las sustracciones (restas).
- Siempre debes resolverlo de izquierda a derecha.
Podemos hablar entonces de la regla MDAS, como una forma de recordar la jerarquía de operaciones.

Por ejemplo, cuando tenemos una operación planteada como la siguiente:
5 + 3 x 9 = ?
- Si ignoramos la regla MDAS, lo resolvemos así:
5 + 3 x 9 = ?
8 x 9 = 72
- Ahora resolveremos la operación siguiendo la regla MDAS
| 5 + 3 x 9 | Multiplicación |
| 5 + 27 = 32 | Adición |
- El resultado correcto de esta operación es 32.
Mira este otro ejemplo de jerarquización de operaciones.
- Recuerda que vamos de izquierda a derecha, empezando con Multiplicación y División, para luego realizar Adiciones y Sustracciones.
- Esta vez resolveremos lo siguiente:
16 + 3 – 45 ÷ 5 + 27 x 2
| 16 + 3 – 45 ÷ 5 + 27 x 2 | De izquierda a derecha. División. |
| 16 + 3 – 9 + 27 x 2 | De izquierda a derecha. Multiplicación. |
| 16 + 3 – 9 + 54 | De izquierda a derecha. Adición. |
| 19 – 9 + 54 | De izquierda a derecha. Sustracción. |
| 10 + 54 = 64 | De izquierda a derecha. Adición. |
Cómo se aplica la ley de jerarquía de las operaciones básicas paso a paso
La jerarquía de operaciones se aplica siguiendo la ley MDAS que vimos en el apartado anterior.
Recuerda que primero realizamos las multiplicaciones y divisiones, y después pasamos a realizar las adiciones y sustracciones.
Además, comenzamos de izquierda a derecha.
En este apartado verás ejercicios resueltos de jerarquía de las operaciones básicas paso a paso.
Ejemplo 1:
65 + 7 – 40 + 3
| Observa que en este ejemplo no tenemos ni multiplicaciones ni divisiones. Entonces, vamos a sumar o a restar de izquierda a derecha. |
- Veamos:
| Operación | Procedimiento seguido |
| 65 + 7 – 40 + 3 | De izquierda a derecha: Adición |
| 72 – 40 + 3 | De izquierda a derecha: Sustracción |
| 32 + 3 = 35 | De izquierda a derecha: Adición |
Ejemplo 2:
26 – 42 ÷ 6 + 3 x 5
En este caso sí tenemos multiplicaciones y divisiones. Entonces: ● Vamos a resolver las multiplicaciones y las divisiones primero, siempre de izquierda a derecha. ● Luego, vamos con las sumas y las restas, también de izquierda a derecha. | 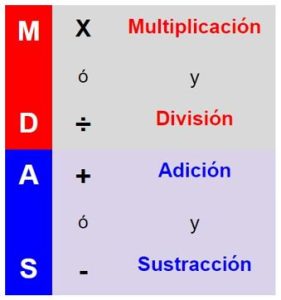 |
- Observa:
| Operación | Procedimiento seguido |
| 26 – 42 ÷ 6 + 3 x 5 | De izquierda a derecha: División |
| 26 – 7 + 3 x 5 | De izquierda a derecha: Multiplicación |
| 26 – 7 + 15 | De izquierda a derecha: Sustracción |
| 19 + 15 = 34 | De izquierda a derecha: Adición |
Ejemplo 3:
94 – 6 x 7 + 5 x 8 – 12 ÷ 4
- Aquí seguiremos con la regla MDAS, tal como lo hemos hecho en el ejemplo anterior.
- Vamos a resolverlo paso a paso:
| Operación | Procedimiento seguido |
| 94 – 6 x 7 + 5 x 8 – 12 ÷ 4 | De izquierda a derecha: Multiplicación |
| 94 – 42 + 5 x 8 – 12 ÷ 4 | De izquierda a derecha: Multiplicación |
| 94 – 42 + 40 – 12 ÷ 4 | De izquierda a derecha: División |
| 94 – 42 + 40 – 3 | De izquierda a derecha: Sustracción |
| 52 + 40 – 3 | De izquierda a derecha: Adición |
| 92 – 3 = 89 | Sustración |
Ejemplo 4:
36 + 2 – 5 x 7 + 6 ÷ 3 + 2
| En este ejercicio debes tener presente, como siempre, la regla MDAS que vimos anteriormente. |
- Observa cómo lo resolvemos:
| Operación | Procedimiento seguido |
| 36 + 2 – 5 x 7 + 6 ÷ 3 + 2 | De izquierda a derecha: Multiplicación |
| 36 + 2 – 35 + 6 ÷ 3 + 2 | De izquierda a derecha: División |
| 36 + 2 – 35 + 2 + 2 | De izquierda a derecha: Adición |
| 38 – 35 + 2 + 2 | De izquierda a derecha: Sustracción |
| 3 + 2 + 2 | De izquierda a derecha: Adición |
| 5 + 2 = 7 | Adición |
Ejemplo 5:
7 x 7 + 81 ÷ 3 – 54 ÷ 6 +25
| Ten en cuenta la regla MDAS. |
Veamos este paso a paso:
| Operación | Procedimiento seguido |
| 7 x 7 + 81 ÷ 3 – 54 ÷ 6 +25 | De izquierda a derecha: Multiplicación |
| 49 + 81 ÷ 3 – 54 ÷ 6 +25 | De izquierda a derecha: División |
| 49 + 27 – 54 ÷ 6 +25 | De izquierda a derecha: División |
| 49 + 27 – 9 +25 | De izquierda a derecha: Adición |
| 76 – 9 +25 | De izquierda a derecha: Sustracción |
| 67 +25 = 92 | Adición |
Jerarquía de operaciones ejemplos
Recuerda que para resolver una operación combinada en la que no existen signos de agrupación, realizamos lo siguiente:
- Resolvemos las multiplicaciones y divisiones, si existen, de izquierda a derecha.
- Resolvemos las adiciones y las sustracciones, si las hay, de izquierda a derecha.
Veamos algunos ejemplos.
Ejemplo 1:
8 + 2 x 3 + 7 – 6 ÷ 2 =
| Operación | Procedimiento realizado |
8 + 2 x 3 + 7 – 6 ÷ 2 = 8 + 6 + 7 – 3 | Primero realizamos las multiplicaciones y divisiones de izquierda a derecha: 2 x 3 = 6 6 ÷ 2 = 3 |
= 8 + 6 + 7 – 3 = 14 + 7 – 3 = 21 – 3 = 18 | Luego realizamos las adiciones y sustracciones de izquierda a derecha: 8 + 6 = 14 14 + 7 = 21 21 – 3 = 18 |
Ejemplo 2:
56 + 9 x 8 – 6 x 5 + 9 : 3 – 32 : 8 =
| Operación | Procedimiento realizado |
56 + 9 x 8 – 6 x 5 + 9 : 3 – 32 : 8 = = 56 + 72 – 30 + 3 – 4 | Iniciamos realizando de izquierda a derecha las multiplicaciones y divisiones: 9 x 8 = 72 6 x 5 = 30 9 : 3 = 3 32 : 8 = 4 |
= 56 + 72 – 30 + 3 – 4 = 128 – 30 + 3 – 4 = 98 + 3 – 4 = 101 – 4 = 97 | Ahora realizamos de izquierda a derecha las adiciones y sustracciones: 56 + 72 = 128 128 – 30 = 98 98 + 3 = 101 101 – 4 = 97 |
Ejemplo 3:
2 + 19 + 23 x 12 – 14 : 2 x 3 – 5 x 12 + 8 + 9 x 6 =
| Operación | Procedimiento realizado |
2 + 19 + 23 x 12 – 14 : 2 x 3 – 5 x 12 + 8 + 9 x 6 = = 2 + 19 + 276 – 21 – 60 + 8 + 54 | Primero hacemos las multiplicaciones y divisiones de izquierda a derecha. 23 x 12 = 276 14 : 2 x 3 = 7 x 3 = 21 5 x 12 = 60 9 x 6 = 54 |
= 2 + 19 + 276 – 21 – 60 + 8 + 54 = 21 + 276 – 21 – 60 + 8 + 54 = 297 – 21 – 60 + 8 + 54 = 276 – 60 + 8 + 54 = 216 + 8 + 54 = 224 + 54 = 278 | Realizamos de izquierda a derecha las adiciones y sustracciones: 2 + 19= 21 21 + 276 = 297 297 – 21 = 276 276 – 60 = 216 216 + 8 = 224 224 + 54 = 278 |
Problemas resueltos de ley de jerarquía de operaciones
Las operaciones combinadas son muy útiles en la vida cotidiana, son muchos los problemas que puedes resolver aplicando la jerarquía de las operaciones.
Veamos algunos casos en los que podemos aplicar los principios que hemos estudiado hasta el momento.
Problema 1
- En un partido de baloncesto se han vendido un total de 1.200 entradas, de las cuales, 525 se han vendido a 32 euros cada una; 490 entradas a 28 euros cada una y el resto a 23 euros cada una. ¿Cuál ha sido el total recaudado en dicho partido?
- Lo primero que haremos será traducir la información a dada a términos aritméticos.
| Operación | Procedimiento realizado |
| 525 x 32 | 525 entradas de 32 euros cada una, se traduce como 525 x 32. |
| 490 x 28 | 490 entradas de 28 euros cada una se escribe como 490 x 28. |
| 1.200 – (525 + 490) = 1.200 + 1.015 = 185 | Restamos 1.200 y 1.015 para saber cuántas entradas cuestan 23 euros. 185 entradas de 23 euros cada una. |
| 185 x 23 | 185 entradas de 23 euros cada una se escribe como 185 x 23. |
525 x 32 + 490 x 28 + 185 x 23 = = 16.800 + 13.720 + 4.255 | Sumamos 525 x 32 + 490 x 28 + 185 x 23. Luego, de izquierda a derecha realizamos las multiplicaciones. |
| 16.800 + 13.720 + 4.255 = 34.775 | De izquierda a derecha realizamos las adiciones. |
- El total recaudado en el partido fue de 34.775 euros.
Problema 2
- Hoy Manuel compró 4 camisetas por 17 euros cada una, 3 pantalones por 23 euros cada una y 2 mochilas por 31 euros cada una. Al llegar a la caja la chica le informó que le harían un descuento de 12 euros. ¿Cuánto canceló Manuel luego de aplicado el descuento?
| Operación | Procedimiento realizado |
| 4 x 17 | 4 camisetas de 17 euros cada una se escribe como 4 x 17. |
| 3 x 23 | 3 pantalones de 23 euros cada uno se traduce como 3 x 23. |
| 2 x 31 | 2 mochilas de 31 euros cada una se escribe como 2 x 31. |
| 4 x 17 + 3 x 23 + 2 x 31 | Sumamos 4 x 17 más 3 x 23 más 2 x 31. |
| 4 x 17 + 3 x 23 + 2 x 31 – 12 | Restamos el descuento de 12 euros |
4 x 17 + 3 x 23 + 2 x 31 – 12 = = 68 + 69 + 62 -12 | De izquierda a derecha resolvemos las multiplicaciones. |
| 68 + 69 + 62 -12 = 187 | De izquierda a derecha resolvemos las adiciones y sustracciones. |
- Manuel canceló 187 euros en total.
Problema 3
- Juan tenía en su billetera 6 billetes de 50 euros y 4 billetes de 20 euros. El fin de semana decidió ir con este dinero al centro comercial y compró un balón de fútbol por 35 euros y una cámara de audio y video por 250 euros. ¿Con cuánto dinero se quedó Juan Pablo luego de cancelar el balón y la cámara?
| Operación | Procedimiento realizado |
| 6 x 50 y 4 x 20 | Seis billetes de 50 euros y cuatro de 20 euros, se escribe matemáticamente así: 6 x 50 y 4 x 20. |
| 6 x 50 + 4 x 20 | 6 x 50 + 4 x 20 es la cantidad de dinero que tiene Juan Pablo. |
| 6 x 50 + 4 x 20 – 35 – 250 | 6 x 50 + 4 x 20 – 35 – 250 es la cantidad de dinero que tiene Juan Pablo menos lo que gastó en el balón y la cámara. |
6 x 50 + 4 x 20 – 35 – 250 = = 300 + 80 – 35 – 250 | Resolviendo las multiplicaciones de izquierda a derecha. |
300 + 80 – 35 – 250 = 380 – 35 -250 = 380 – 35 – 250 = 345 – 250 = 95 | Realizando las adiciones y sustracciones de izquierda a derecha |
- Juan después de pagar el balón y la cámara se quedó con 95 euros.
Ley de jerarquía de operaciones básicas con paréntesis
Las operaciones básicas con paréntesis son expresiones numéricas en las que se combinan varias operaciones (sumas, restas, multiplicaciones y divisiones).
Para resolver las operaciones básicas con paréntesis hay que cumplir unos sencillos pasos:
- Resolver primero las operaciones que estén dentro del paréntesis
- Si aparecen varias operaciones seguidas, primero se hacen las multiplicaciones y divisiones y luego las adiciones y sustracciones.
Veamos algunos ejemplos de operaciones básicas con paréntesis:
Ejemplo 1:
(8 x 9) – (12 + 5 – 8) + 15 =
| Operación | Procedimiento realizado |
| (8 x 9) – (12 + 5 – 8) + 15 = 72 – 9 + 15 | Resolvemos las operaciones que están dentro del paréntesis. (8 x 9) = 72 (12 + 5 – 8) = 9 |
| 72 – 9 + 15 = 63 +15 = 78 | Realizamos las adiciones y sustracciones de izquierda a derecha. |
Ejemplo 2:
5 x (9 x 12 – 18) – (15 : 3 – 1) =
| Operación | Procedimiento realizado |
5 x (9 x 12 – 18) – (15 : 3 – 1) + 15 = = 5 x 90 – 4 +15 | Resolvemos las operaciones que están dentro del paréntesis. (9 x 12 – 18) = 108 – 18 = 90 (15 : 3 – 1) = 5 – 1 = 4 |
5 x 90 – 4 + 15 = 450 – 4 +15 = 461 | De izquierda a derecha realizamos primero la multiplicación y luego la sustracción y la adición. |
Ejemplo 3:
2 x 3 + (81 : 9 – 5 + 3 x 2) – (6 x 3 – 24 : 2) + 1 =
| Operación | Procedimiento realizado |
2 x 3 + (81 : 9 – 5 + 3 x 2) – (6 x 3 – 24 : 2) + 1 =
= 2 x 3 + 10 – 6 + 1 | Resolvemos las operaciones que están dentro del paréntesis. (81 : 9 – 5 + 3 x 2) = 9 -5 + 6 = 10 (6 x 3 – 24 : 2) = 18 – 12 = 6 |
2 x 3 + 10 – 6 + 1 = = 6 + 10 – 6 + 1 = 11
| De izquierda a derecha realizamos primero la multiplicación y luego las adiciones y sustracciones. |
Ley de jerarquía de operaciones básicas con paréntesis y corchetes.
Las operaciones básicas con paréntesis y corchetes combinan adiciones, sustracciones, multiplicaciones y divisiones.
Para resolver las operaciones básicas con paréntesis y corchetes hay que cumplir unos pasos muy sencillos. :
- Resolver primero las operaciones que estén dentro del paréntesis.
- Luego se realizan las operaciones que están dentro del corchete.
- Si aparecen varias operaciones seguidas, primero se hacen las multiplicaciones y divisiones y luego las adiciones y sustracciones.
Veamos algunos ejemplos de operaciones básicas con paréntesis y corchetes:
Ejemplo 1:
20 + [15 + (15 – 6) + 39]
| Operación | Procedimiento realizado |
20 + [15 + (15 – 6) + 39] = =20 + [15 + 9 +39] | Resolvemos la operación que está dentro del paréntesis. (15 – 6) = 9 |
= 20 + [15 + 9 + 39] = = 20 + 63 | Ahora resolvemos las adiciones que están dentro de los corchetes. |
| = 20 + 63 = 83 | Por último, hacemos: 20 + 63 = 83 |
Ejemplo 2:
[ 13 + (68 -24)] – (95 – 48)] + [6 + 7 +(72 -12) -23]
| Operación | Procedimiento realizado |
[ 13 + (68 -24)] – (90 – 48)] + [6 + 7 + (72 -12) – 23]= = [13 + 44 – 42] + [6 + 7 +60 – 23] | Resolvemos las operaciones que están dentro del paréntesis. (68 – 24) = 44 (90 – 48) = 42 (72 – 12) = 60 |
= [13 + 44 – 42] + [6 + 7 +60 – 23] = 15 + 52 | Luego, realizamos las operaciones que se encuentran dentro de los corchetes. |
| 15 + 52 = 67 | Y finalizamos con: 15 + 52 = 67 |
Ejemplo 3:
3 x [ 9 – 5 + (3 x 5 – 6) – (2 + 15 : 3)] – [ (8 x 6 : 12) + (6 x 1)]
| Operación | Procedimiento realizado |
3 x [9 – 5 + (3 x 5 – 6) – (2 + 15 : 3)] -[ (8 x 6 : 12) + (6 x 1)] = = 3 x [9 – 5 + 9 – 7] – [4 + 6] | Resolvemos las operaciones que están dentro del paréntesis. Recuerda hacer primero las multiplicaciones y divisiones de izquierda a derecha. (3 x 5 – 6) = 15 – 6 = 9 (2 + 15 : 3) = 2 + 5 = 7 (8 x 6 : 12) = 48 : 12 = 4 (6 x 1) = 6 |
= 3 x [9 – 5 + 9 – 7] – [4 + 6] = 3 x 6 – 10 | Luego, realizamos las operaciones que se encuentran dentro de los corchetes. |
= 3 x 6 – 10 = = 18 – 10 = 8 | Y finalizamos con: 3 x 6 – 10 = = 18 -10 = 8 Recuerda que realizamos primero la multiplicación y luego la sustracción. |
Ley de jerarquía de operaciones básicas con paréntesis, corchetes y llaves
Las operaciones básicas con paréntesis, corchetes y llaves incorporan tres signos de agrupación y combinan operaciones como la adición, sustracción, multiplicación y división.
Para realizar las operaciones básicas con paréntesis, corchetes y llaves hay que considerar los siguientes pasos:
- Resolver primero las operaciones que estén dentro del paréntesis.
- Luego se realizan las operaciones que están dentro del corchete.
- Seguidamente se resuelven las operaciones que se encuentran entre las llaves.
- Si aparecen varias operaciones seguidas, primero se hacen las multiplicaciones y divisiones y luego las adiciones y sustracciones.
Veamos algunos ejemplos de operaciones básicas con paréntesis, corchetes y llaves:
Ejemplo 1:
6 + {4 + 9 x [18 : 3 – 2 + 5 x (7 + 3 x 4)] + (4 x 2)} + (7 x 3)
| Operación | Procedimiento realizado |
6+{4 + 9 x [18 : 3 – 2 + 5 x (7 + 3 x 4)]+(4 x 2)}+(7 x 3) = = 6 + {4 + 9 x [18 : 3 – 2 + 5 x 19] + 8} + 21 | Resolvemos las operaciones que están dentro del paréntesis. Recuerda hacer primero las multiplicaciones y divisiones de izquierda a derecha. (7 + 3 x 4) = 7 + 12 =19 (4 x 2) = 8 (7 x 3) = 21 |
= 6 + {4 + 9 x [18 : 3 – 2 + 5 x 19] + 8} + 21 = 6 + { 4 + 9 x [ 6 – 2 + 95] + 8} + 21 = 6 + { 4 + 9 x 99 + 8} + 21 | Ahora, realizamos las operaciones que se encuentran dentro de los corchetes. |
= 6 + { 4 + 9 x 99 + 8} + 21 = 6 + { 4 + 891 + 8} + 21 = 6 + 903 + 21 | Luego resolvemos las operaciones entre las llaves. Recuerda realizar primero las multiplicaciones y divisiones de izquierda a derecha. |
| = 6 + 903 + 21 = 930 | Finalizamos con: 6 + 903 + 21 = 930 |
Ejemplo 2
{ 5 + [ 9 : 3 + 6 x 5 + (23 – 8 : 2 + 5) + 7 x (5 + 6) – 1] + 6 x 10}
| Operación | Procedimiento realizado |
{5 + [9 : 3 + 6 x 5 + (23 – 8:2 + 5) + 7x (5 + 6) – 1] + 6 x 10} = {5 + [9 : 3 + 6 x 5 + 24 + 7 x 11 – 1] + 6 x 10} | Realizamos las operaciones que están dentro del paréntesis. Recuerda hacer primero las multiplicaciones y divisiones de izquierda a derecha. (23 – 8 : 2 + 5) = =23 – 4 + 5 = 24 (5 + 6) =11 |
= {5 + [9 : 3 + 6 x 5 + 24 + 7 x 11 – 1] + 6 x 10} = {5 + [3 + 30 + 24 + 77 – 1] + 6 x 10 = { 5 + 133 + 6 x 10} | A continuación, realizamos las operaciones que se encuentran dentro de los corchetes. |
= { 5 + 133 + 6 x 10} = { 5 +133 + 60} = 198 | Resolvemos las operaciones entre las llaves. Recuerda realizar primero las multiplicaciones y divisiones de izquierda a derecha. |
Ejemplo 3:
2 + 9 x {8 + 5 x [4 + 8 x 4 – 2 x (2 x 3) + 5] – 1} + 4 x [100 : 5 – 3 x (2 x 3)]
| Operación | Procedimiento realizado |
2 + 9 x {8 + 5 x [4 + 8 x 4 – 2 x (2 x 3) + 5] – 1} + 4 x [100 : 5 – 3 x (2 x 3)] = = 2 + 9 x {8 + 5 x [4 + 8 x 4 – 2 x 6 + 5] – 1} + 4 x [100 : 5 – 3 x 6] | Resolvemos las operaciones que están dentro del paréntesis. (2 x 3) =6 (2 x 3) =6 |
= 2 + 9 x {8 + 5 x [4 + 8 x 4 – 2 x 6 + 5] – 1} + 4 x [100 : 5 – 3 x 6] = 2 + 9 x {8 + 5 x [4 + 32 – 12 + 5] – 1} + 4 x [20 – 18] = 2 + 9 x {8 + 5 x 29 – 1} + 8 | Luego realizamos las operaciones que se encuentran dentro de los corchetes. Recuerda realizar primero las multiplicaciones y divisiones, siempre de izquierda a derecha. |
= 2 + 9 x {8 + 5 x 29 – 1} + 8 = 2 + 9 x {8 + 145 – 1} + 8 = 2 + 9 x 152 + 8 | Resolvemos las operaciones entre las llaves. Recuerda realizar primero las multiplicaciones y divisiones de izquierda a derecha. |
= 2 + 9 x 152 + 8 = 2 + 1.368 + 8 = 1.378 | Terminamos resolviendo 2 + 9 x 152 + 8 = 1.378 |
Ejercicios resueltos de ley de jerarquía con signos de agrupación
Recuerda que para resolver ejercicios de operaciones básicas en los que se encuentren signos de agrupación seguimos los siguientes pasos:
| 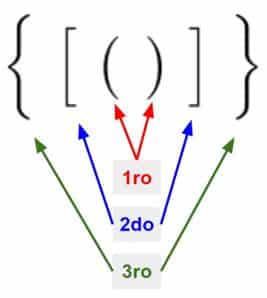 |
Recuerda que, al resolver las operaciones dentro de cada signo de agrupación, debes seguir la regla MDAS:
- Empiezas de isquierda a derecha.
- Primero las Multiplicaciones y Divisiones.
- Después las Sumas y Restas.
Ejercicio 1
10 + { ( 2 × 5 ) + [ 8 + (7 – 2) ] }
| Operación | Procedimiento |
| 10 + { ( 2 × 5 ) + [ 8 + (7 – 2) ] } | Resolvemos las operaciones que están entre los paréntesis. |
| 10 + { 10 + [ 8 + 5 ] } | Resolvemos las operaciones que están entre los corchetes. |
| 10 + { 10 + 13 } | Resolvemos las operaciones que están entre las llaves. |
| 10 + 23 = 33 | Sumamos. |
Ejercicio 2
5 x 5 – {16 ÷ 2 – (3 – 1) – [15 – (2 x 5) ] + 16}
| Operación | Procedimiento |
| 5 x 5 – {16 ÷ 2 – (3 – 1) – [15 – (2 x 5) ] + 21} | Resolvemos las operaciones que están entre los paréntesis. |
| 5 x 5 – {16 ÷ 2 – 2 – [15 – 10 ] + 21} | Resolvemos las operaciones que están entre los corchetes. |
| 5 x 5 – {16 ÷ 2 – 2 – 5 + 21} | Resolvemos, de izquierda a derecha, las operaciones que están entre las llaves. |
| 5 x 5 – {8 – 2 – 5 + 21} | Resolvemos, de izquierda a derecha, las operaciones que están entre las llaves. |
| 5 x 5 – {6 – 5 + 21} | Resolvemos, de izquierda a derecha, las operaciones que están entre las llaves. |
| 5 x 5 – {1 + 21} | Resolvemos, de izquierda a derecha, las operaciones que están entre las llaves. |
| 5 x 5 – 22 | Resolvemos las operaciones de izquierda a derecha. |
| 25 – 22 = 3 | Restamos. |
Ejercicio 3
17 + { (8 x 3 – 4 + 7) – [ 5 – (4 – 2) ] – 1 } + 2 x 5
| Operación | Procedimiento |
| 17 + { (8 x 3 – 4 + 7) – [ 5 – (4 – 2) ] – 1 } + 2 x 5 | Resolvemos, de izquierda a derecha, las operaciones que están entre los paréntesis. |
| 17 + { (24 – 4 + 7) – [ 5 – 2 ] – 1 } + 2 x 5 | Resolvemos, de izquierda a derecha, las operaciones que están entre los paréntesis. |
| 17 + { (20 + 7) – [ 5 – 2 ] – 1 } + 2 x 5 | Resolvemos, de izquierda a derecha, las operaciones que están entre los paréntesis. |
| 17 + { 27 – [ 5 – 2 ] – 1 } + 2 x 5 | Resolvemos las operaciones que están entre los corchetes. |
| 17 + { 27 – 3 – 1 } + 2 x 5 | Resolvemos, de izquierda a derecha, las operaciones que están entre las llaves. |
| 17 + { 24 – 1 } + 2 x 5 | Resolvemos, de izquierda a derecha, las operaciones que están entre las llaves. |
| 17 + 23 + 2 x 5 | Resolvemos las operaciones que nos quedan respetando la jerarquía. |
| 17 + 23 + 10 | Resolvemos de izquierda a derecha las operaciones. |
| 40 + 10 = 50 | Restamos. |
Ley de jerarquía de operaciones con fracciones y potencias
En este apartado te explicaremos cuál es la jerarquía de las operaciones que debes seguir cuando tienes operaciones combinadas que implican potencias y fracciones.
Al igual que con los números naturales, las operaciones deben realizarse de izquierda a derecha. El orden es el siguiente:
- Raíces y portencias (que pueden ser expresadas con un exponente).
- Multiplicaciones y divisiones.
- Sumas y restas.
| En caso de haber algún signo de agrupación, se sigue igualmente el orden de paréntesis (), corchetes [] y llaves {}. |
Ejemplo 1:
| Operación | Procedimiento |
| Resolvemos las operaciones de izquierda a derecha. | |
| Sumamos fracciones. | |
| Continuamos la suma de fracciones. |
Ejemplo 2:
| Operación | Procedimiento |
| Resolvemos las persaciones de izquierda a derecha. | |
| Dividimos fracciones. | |
| Multiplicamos fracciones. | |
| Simplificamos 4230 por 6 y 1220por 4. | |
| Restamos fracciones de igual denominador. |
Ejemplo 3:
| Operación | Procedimiento |
| Resolvemos, de izquierda a derecha, las potencias y las raíces. | |
| Resolvemos, de izquierda a derecha, las potencias y las raíces. | |
| Resolvemos la operación que está dentro del corchete. | |
| Sumamos fracciones. | |
| Dividimos fracciones y simplificamos la fracción 18090 por 2. |
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇

Definición de jerarquía de las operaciones

Relgas básicas de la jerarquía de las operaciones

Jerarquía con signos de agrupaciones

Aplicación de la jerarquía de operaciones

Operaciones combinadas en problemas

Definición de jerarquía de las operaciones

Relgas básicas de la jerarquía de las operaciones

Jerarquía con signos de agrupaciones

Aplicación de la jerarquía de operaciones

Operaciones combinadas en problemas