Frecuencia absoluta
Cuando observamos un conjunto de datos necesitamos de varias herramientas y conceptos estadísticos para poder interpretarlos de manera correcta. Uno de los más utilizados es la frecuencia, y más específicamente la frecuencia absoluta.
En este artículo aprenderás a interpretar datos usando la frecuencia absoluta. Conocerás qué es la frecuencia absoluta y cómo sacarla, ejemplos de frecuencia absoluta para datos agrupados y para datos no agrupados. Además, aprenderás acerca de la frecuencia acumulada con ejemplos.
Qué es la frecuencia absoluta
Recuerda que una variable cualitativa es aquella que expresa características o cualidades que no pueden ser medidas usando números, como la red social preferida, el color de los ojos, el lugar de nacimiento, etc.
Por ejemplo, estos son los ojos de un grupo de personas. Nos fijaremos en el color de ojos, esa será nuestra variable. Observa:

Como puedes ver, la variable cualitativa “color de ojos” toma los valores “marrón”, “verde” y “azul”.
En este caso obtuvimos 9 datos y las veces que se repite cada valor, es decir, la frecuencia absoluta de cada valor es el siguiente:
| Color de ojos | Frecuencia absoluta (veces que aparece) |
| Marrón | 4 |
| Verde | 2 |
| Azul | 3 |
Una variable cuantitativa, por su parte, es aquella cuyo valor puede expresarse en números. Algunos ejemplos son: peso, talla, edad, número de hermanos, etc.
Por ejemplo, aquí aparecen un grupo de niños que están diciendo su edad. Nos fijaremos en esa variable: la edad.
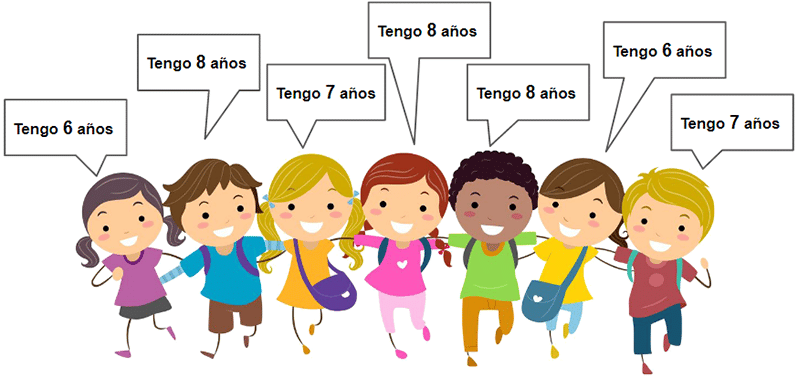
Obtuvimos 7 datos de la variable cuantitativa “edad”. Como puedes ver, esta variable toma los siguientes valores: 6, 7 y 8.
La frecuencia absoluta de cada valor es el siguiente:
| Edad en años | Frecuencia absoluta (veces que aparece) |
| 6 | 2 |
| 7 | 2 |
| 8 | 3 |
| Total | 7 |
Cómo sacar la frecuencia absoluta
Para calcular la frecuencia absoluta debemos:
- Reconocer cuál es la variable que estamos observando en el conjunto de datos.
- Hacer una lista de los valores que toma la variable.
- Contar y totalizar las veces que aparece cada valor.
- Realizar una tabla para resumir los datos.
Veamos esto con un ejemplo.
Los datos que presentamos a continuación muestran los tipos de sangre reportados de 40 personas:
| AB | A | B | O | A | A | A | B | O | AB |
| B | O | B | B | B | A | A | A | AB | B |
| O | A | A | A | A | AB | O | B | B | AB |
| O | B | O | O | A | A | O | B | AB | AB |
- Vamos a sacar la frecuencia absoluta de este conjunto de datos.
- Variable que estamos observando:
- La variable es tipo de sangre, y es una variable cualitativa.
- Los valores que toma la variable son:
- AB
- A
- B
- O
- Que son los 4 tipos de sangre principales.
- Ahora a contar y totalizar las veces que aparece cada valor:
- Variable que estamos observando:
| AB | A | B | O | A | A | A | B | O | AB |
| B | O | B | B | B | A | A | A | AB | B |
| O | A | A | A | A | AB | O | B | B | AB |
| O | B | O | O | A | A | O | B | AB | AB |
| Tipo de sangre | Conteo | SubTotal |
| AB | 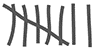 | 7 |
| A | 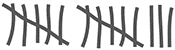 | 13 |
| B | 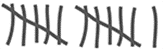 | 11 |
| O | 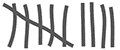 | 9 |
| Total | 40 | |
- Representemos estos datos en una tabla.
- La tabla para representar la frecuencia absoluta debe contener dos columnas: una columna con los valores que toma la variable y otra columna con la frecuencia absoluta de ese valor.
- A la variable, generalmente, se le asigna la letra x y a la frecuencia se le asigna la letra f. Observa:
| Tipo de sangre (X) | Frecuencia (f) |
| AB | 7 |
| A | 13 |
| B | 11 |
| O | 9 |
| Total | 40 |
- Hemos calculado la frecuencia absoluta de cada valor de la variable tipo de sangre en los 40 datos que teníamos.
Frecuencia absoluta ejemplos
En este apartado veremos varios ejemplos de frecuencia absoluta para que comprendas mejor este concepto.
Ejemplo 1:
- En una encuesta a 30 personas acerca de su zumo de frutas favorito se obtuvieron las siguientes respuestas:
 |  |  |  |  |  |  |  | ||
 |  |  |  |  |  |  |  | ||
 |  |  |  |  |  |
- Vamos a elaborar la tabla de frecuencia correspondiente.
- La variable es zumo de frutas, y los valores que puede tomar la variable son:
- Zumo de manzana
- Zumo de tomate
- Zumo de naranja
- Zumo de zanahoria
- Zumo de piña
- Vamos a contar cuántas veces aparece cada valor:
| Zumo de frutas | Conteo | Frecuencia |
| Zumo de manzana | 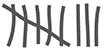 | 8 |
| Zumo de tomate | 4 | |
| Zumo de naranja | 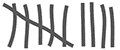 | 9 |
| Zumo de zanahoria | 3 | |
| Zumo de piña | 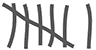 | 6 |
| Total | 30 | |
Ahora podemos elaborar la tabla de frecuencia absoluta:
| Zumo de fruta (x) | Frecuencia (f) |
| Zumo de manzana | 8 |
| Zumo de tomate | 4 |
| Zumo de naranja | 9 |
| Zumo de zanahoria | 3 |
| Zumo de piña | 6 |
| Total | 30 |
Ejemplo 2:
- El número de veces que han ido a la playa en el último mes un grupo de estudiantes de una clase es:
| 2 | 3 | 0 | 1 | 5 |
| 3 | 2 | 1 | 0 | 0 |
| 2 | 1 | 2 | 3 | 5 |
| 0 | 5 | 4 | 1 | 1 |
| 1 | 2 | 0 | 1 | 2 |
- Elaboramos la tabla de frecuencia absoluta correspondiente teniendo en cuenta que:
- La variable es “veces que ha ido a la playa”.
- Los valores que toma la variable son 0, 1, 2, 3, 4, 5.
- Hemos usado colores para ayudarnos a contar.
- Después de contar y totalizar, la tabla quedaría así:
- Elaboramos la tabla de frecuencia absoluta correspondiente teniendo en cuenta que:
| Veces que ha ido a la playa (x) | Frecuencia (f) |
| 0 | 5 |
| 1 | 7 |
| 2 | 6 |
| 3 | 3 |
| 4 | 1 |
| 5 | 3 |
| Total | 25 |
Frecuencia absoluta para datos no agrupados. Ejemplos
Como ya hemos explicado la frecuencia absoluta es el número de veces que aparece un dato en un estudio estadístico.
Por otro lado, los datos no agrupados son aquellos que son registrados tal y como han sido recogidos de la muestra o fenómeno que se desea analizar. Por las características de estos valores no es necesario agruparlos en clases.
Por ejemplo:
- Las edades de 10 niños de una clase:7, 7, 8, 6, 6, 7, 7, 7, 8, 6.
- Las calificaciones del examen final de matemáticas de 15 estudiantes de Segundo de la ESO: 6, 7, 9, 9, 5, 6, 8, 8, 7, 5, 10, 8, 6, 8, 10.
- EL color preferido de 12 niños: azul, naranja, rojo, azul, verde, naranja, azul, amarillo, rojo, amarillo, verde, naranja.
La frecuencia absoluta para datos no agrupados es una distribución que señala el número de veces que aparecen los datos estadísticos.
En este tipo de distribuciones cada dato se presenta tal y como ha sido recogido de la muestra o proceso que se quiere estudiar.
Veamos a continuación dos ejemplos de frecuencia absoluta para datos no agrupados:
Ejemplo 1:
- Se le solicitó a un grupo de adolescentes que indiquen su género musical preferido, las respuestas obtenidas fueron las siguientes:
| Pop | Salsa | Pop | Heavy |
| Salsa | Pop | Heavy | Salsa |
| Reguetón | Heavy | Salsa | Pop |
| Pop | Pop | Pop | Reguetón |
- Con estos resultados vamos a elaborar una tabla de frecuencias absolutas.
- En la primera columna, colocamos los valores de la variable (en este caso la variable es género musical y es de tipo cualitativa) y en la segunda columna escribimos la frecuencia absoluta.
| Género musical (x) | Frecuencia absoluta (f) |
| Pop | 7 |
| Salsa | 4 |
| Heavy | 3 |
| Reguetón | 2 |
| Total | 16 |
- En este caso hemos construido una tabla de frecuencias absolutas que nos permite saber el número de adolescente que prefiere cada uno de los géneros musicales que aparecen en el estudio. A partir de la tabla también podemos conocer el número total de adolescentes que participaron en el estudio, que en este caso fue 16.
Ejemplo 2:
- Los siguientes datos corresponden a las calificaciones finales del curso de matemáticas en verano. Las notas estuvieron entre 1 y 10 puntos.
| 5 | 8 | 9 | 2 | 4 | 7 |
| 8 | 9 | 10 | 6 | 6 | 2 |
| 7 | 9 | 7 | 5 | 4 | 3 |
| 1 | 2 | 10 | 8 | 7 | 2 |
- En la primera columna, colocamos los valores de nuestra variable en la segunda la frecuencia absoluta. Hemos resaltado con colores para facilitar el conteo.
| Calificaciones finales (x) | Frecuencia absoluta (f) |
| 1 | 1 |
| 2 | 4 |
| 3 | 1 |
| 4 | 2 |
| 5 | 2 |
| 6 | 2 |
| 7 | 4 |
| 8 | 3 |
| 9 | 3 |
| 10 | 2 |
| Total | 24 |
- La tabla de frecuencias absolutas que acabamos de construir presenta de forma organizada la información referida a las calificaciones finales del curso de matemáticas. Podemos ver que las calificaciones que más se repiten son 2 y 7. Mientras que las de menor frecuencia son 1 y 3.
Frecuencia absoluta para datos agrupados. Ejemplos.
Cuando la variable toma una gran cantidad de valores, o cuando la variable es continua, utilizamos tablas de frecuencia con datos agrupados.
Por ejemplo:
- Las edades de 40 personas que asisten a una escuela de baile. En este caso la variable toma 40 valores, al ser muy grande el número de datos conviene hacer una tabla de frecuencias con datos agrupados.
- La altura de 30 adolescentes que asisten a una escuela de baloncesto. La altura de los adolescentes de este ejemplo, es una variable continua porque puede tomar muchísimos valores entre 1m y 2m, por eso es conveniente agrupar las estaturas en intervalos.
Ahora veamos dos ejemplos de tablas de frecuencia absoluta con datos agrupados.
Ejemplo 1:
- Las edades de 40 personas que asisten a una escuela de baile.
| 35 | 25 | 26 | 28 | 39 | 42 | 51 | 26 | 28 | 31 |
| 23 | 27 | 33 | 37 | 41 | 21 | 26 | 31 | 37 | 45 |
| 21 | 22 | 36 | 38 | 20 | 58 | 59 | 55 | 45 | 24 |
| 59 | 61 | 25 | 64 | 32 | 63 | 37 | 61 | 41 | 40 |
- Completamos la siguiente tabla para organizar los datos suministrados.
- En la tabla que verás a continuación hemos agrupado los datos en intervalos, porque la variable puede tomar valores que están entre 21 y 64.
- Decidimos no registrar estos datos uno por uno, porque la tabla tendría muchísimas filas, lo que complicaría el procesamiento y análisis de la información.
- En la primera columna tenemos los intervalos en los que se han agrupado las edades de las personas que asisten a la escuela de baile.
- En el intervalo [20, 24] hemos incluido a las edades 20, 21, 22, 23 y 24 años. El segundo intervalo [25,29], contiene las edades 25, 26, 27, 28, 29. Y así sucesivamente con el resto de los intervalos.
- En la segunda columna aparece el conteo realizado en cada uno de los intervalos.
- Y finalmente, en la tercera columna tenemos la frecuencia absoluta.
| Intervalo | Conteo | Frecuencia absoluta |
| [20 – 24] | / / / / / / | 6 |
| [25 – 29] | / / / / / / / / | 8 |
| [30 – 34] | / / / / | 4 |
| [35 – 39] | / / / / / / / | 7 |
| [40 – 44] | / / / / | 4 |
| [45 – 49] | / / | 2 |
| [50 – 54] | / | 1 |
| [55 – 59] | / / / / | 4 |
| [60 – 64] | / / / / | 4 |
| Total | 40 | 40 |
Ejemplo 2:
- En este caso trabajaremos con las alturas de 30 adolescentes que asisten a una escuela de baloncesto.
| 1,71 | 1,69 | 1,68 | 1,72 | 1,85 | 1,89 |
| 1,87 | 1,92 | 1,93 | 1,75 | 1,77 | 1,72 |
| 1,76 | 1,79 | 1,81 | 1,68 | 1,87 | 1,73 |
| 1,81 | 1,74 | 1,69 | 1,70 | 1,61 | 1,95 |
| 1,86 | 1,74 | 1,90 | 1,74 | 1,64 | 1,78 |
- Vamos a completar la siguiente tabla a partir de estos datos.
- Nuevamente hemos agrupado los datos en intervalos, porque la variable puede tomar muchísimos valores entre 1,61 y 2,00.
- No los hemos registrado uno por uno, porque el procesamiento y análisis de los datos se complica.
- En la primera columna tenemos los intervalos en los que se han agrupado las alturas de los adolescentes que asisten a la escuela de baloncesto.
- En el intervalo [1,61 – 1,68] están incluidas las siguientes alturas: 1,61 – 1,62 – 1,63 – 1,64 – 1,65 – 1,66 – 1,67 – 1,68.
- El intervalo [1,69 – 1,76] contiene las alturas 1,69 – 1,70 – 1,71 – 1,72 – 1,73 – 1,74 – 1,75 – 1,76.
- Los intervalos [1,77 – 1,84] – [1,85 – 1,92] – [1,93 – 2,00] se comportan de forma similar a los dos primeros.
- En la segunda columna aparece el conteo realizado en cada uno de los intervalos.
- Y finalmente, en la tercera columna tenemos la frecuencia absoluta.
| Intervalo | Conteo | Frecuencia absoluta |
| [1,61 – 1,68] | / / / / | 4 |
| [1,69 – 1,76] | / / / / / / / / / / / / | 12 |
| [1,77 – 1,84] | / / / / / | 5 |
| [1,85 – 1,92] | / / / / / / / | 7 |
| [1,93 – 2,00] | / / | 2 |
| Total | 30 | 30 |
Frecuencia absoluta acumulada. Ejemplos.
Veamos dos ejemplos de frecuencia absoluta acumulada. Utilizaremos dos de las tablas de frecuencias acumuladas que hemos construido anteriormente.
Ejemplo 1:
- Género musical preferido por un grupo de adolescentes latinoamericanos.
| Género musical (x) | Frecuencia absoluta (f) | Frecuencia acumulada |
| Pop | 7 | 7 |
| Salsa | 4 | 7 + 4 = 11 |
| Heavy | 3 | 11 + 3 = 14 |
| Reguetón | 2 | 14 + 2 = 16 |
| Total | 16 |
Ejemplo 2:
- Las alturas de 30 adolescentes que asisten a una escuela de baloncesto.
| Intervalo | Frecuencia absoluta | Frecuencia acumulada |
| [1,61 – 1,68] | 4 | 4 |
| [1,69 – 1,76] | 12 | 4 + 12 = 16 |
| [1,77 – 1,84] | 5 | 16 + 5 = 21 |
| [1,85 – 1,92] | 7 | 21 + 7 = 28 |
| [1,93 – 2,00] | 2 | 28 + 2 = 30 |
| Total | 30 |
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇

Definiciones sobre la frecuencia absoluta

Variables cualitativas y cuantitativas

Cálculo de la frecuencia absoluta

Tablas de frecuencias absolutas

Especificaciones de la frecuencia absoluta

Organización de una tabla de frecuencias

Definiciones sobre la frecuencia absoluta

Variables cualitativas y cuantitativas

Cálculo de la frecuencia absoluta

Tablas de frecuencias absolutas

Especificaciones de la frecuencia absoluta

Organización de una tabla de frecuencias
![]() Registrado en SafeCreative.
Registrado en SafeCreative.
