Antes de adentrarnos en qué son los ejes de simetría debemos aclarar un concepto clave: la simetría.
La simetría
En este artículo verás todo lo que requieres conocer acerca de este hermoso concepto matemático, que es usado tanto dentro de la matemática como fuera de ella.
La simetría es una correspondencia exacta en tamaño, forma y posición de las partes de un objeto con respecto a un eje imaginario.
Esta idea geométrica ayuda a entender fenómenos de la naturaleza y las propiedades de ciertas estructuras, organismos y cuerpos.
Este concepto encuentra aplicación en distintas áreas de la vida como lo son el arte, la química, la arquitectura, la física, la matemática, entre muchas otras.
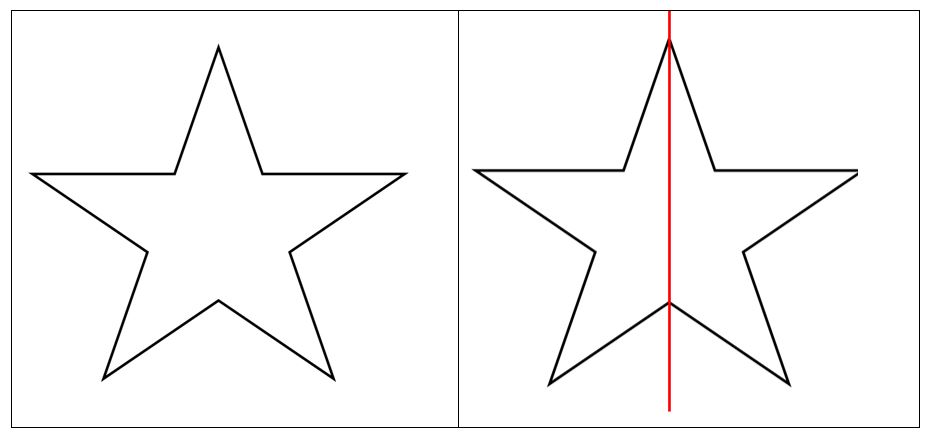
Fíjate que al trazar convenientemente una línea por esta estrella se generan dos figuras idénticas en cuanto a tamaño, forma y posición.
Por lo que se dice que esta estrella es simétrica con respecto a la línea roja que hemos trazado.
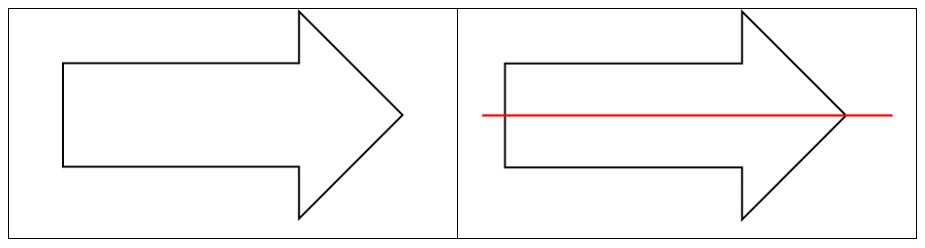
De igual manera ocurre con esta flecha a la que le hemos trazado una línea horizontal, de tal modo que resulten dos figuras iguales en cuanto tamaño, forma y posición. Entonces, la flecha es simétrica con respecto a la línea roja.
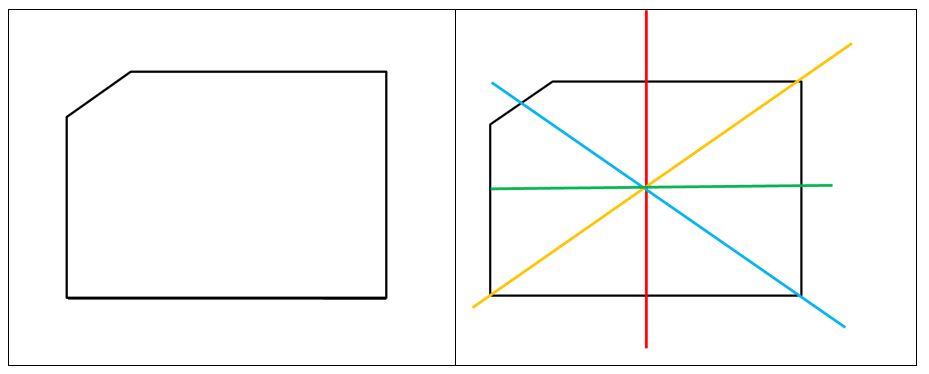
A la siguiente figura le hemos trazado una línea horizontal, otra vertical y dos oblicuas. Fíjate que ninguna de las líneas determina dos partes iguales en cuanto a tamaño, forma y posición, por lo que esta figura no es simétrica o lo que es lo mismo, es asimétrica.
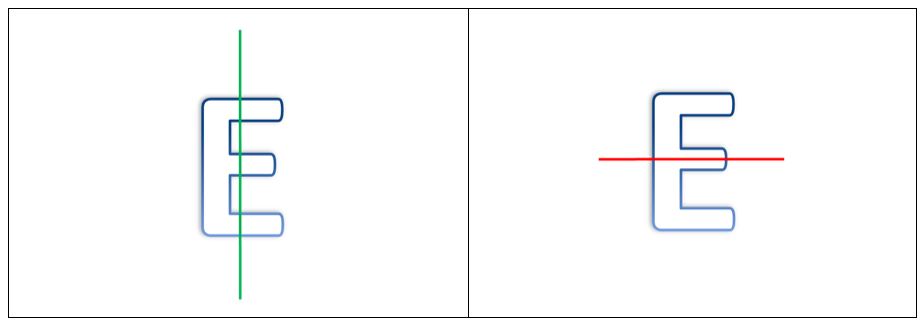
Ahora le toca el turno a la E. Observa que le hemos trazado una línea horizontal y otra vertical. En este caso la línea verde (vertical) no determina dos partes iguales en cuanto tamaño, forma y posición.
Mientras que la línea de color rojo (horizontal) si lo hace. Como la letra tiene al menos un eje de simetría, entonces se dice que es simétrica.
Es tu turno para practicar en esta ficha con el concepto de simetría.
Qué es un eje de simetría y cómo conseguirlo
Para ver si una figura es simétrica, como ya hemos dicho, se dibuja una línea que lo divida en dos lados y que nos permita mostrar una coincidencia perfecta en cada lado, en cuanto a forma, tamaño y posición con respecto a la línea que trazamos.
Es como ver una imagen en el espejo.
Fíjate en esta hermosa mariposa:
La línea azul imaginaria que trazamos en medio de ella la divide en dos mitades que son iguales en forma, tamaño y posición.
A esta línea se le llama eje de simetría.
Un eje de simetría es una línea imaginaria que se traza en una figura y que la divide en dos partes que son iguales en cuanto a forma, posición y tamaño.
Veamos otro ejemplo. Observa esta imagen y las líneas que hemos trazado:
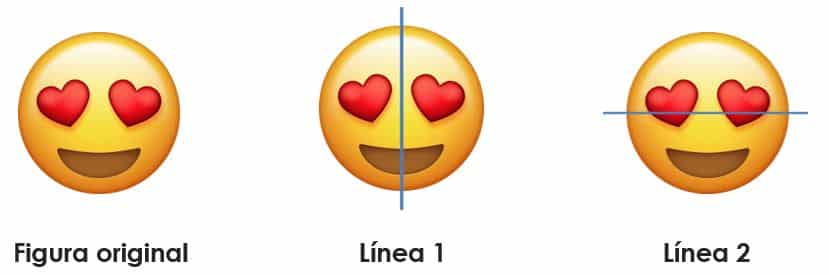
Como puedes observar, a partir de la figura original podemos trazar una línea vertical, que hemos llamado Línea 1, para dividirla en dos partes exactamente iguales.
Con la línea 2 sucede que, aunque divide a la figura en dos partes iguales en tamaño, estas dos partes no son iguales en forma.
Por lo tanto, la Línea 1 es un eje de simetría de la figura mientras que la Línea 2 no es un eje de simetría de la figura.
DOBLANDO EL PAPEL PARA ENCONTRAR LOS EJES DE SIMETRÍA
Toma una hoja de papel de forma cuadrada y ve paso a paso encontrando todos sus ejes de simetría con nosotros.
Eje 1: Primera diagonal
Toma la hoja y dóblala como se muestra en la figura. Verás que las dos partes se superponen de manera exacta.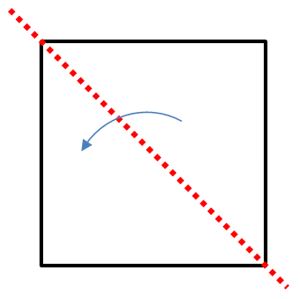
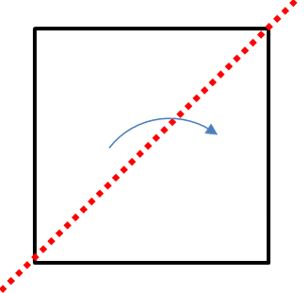Eje 2: Segunda diagonal
Ahora hagamos un doblez similar a partir de la otra diagonal del cuadrado. Puedes comprobar que las dos partes son iguales. De hecho son triángulos congruentes.
Eje 3: Punto medio de los lados – 1
Ahora vamos a doblar de arriba hacia abajo, haciendo coincidir los bordes de la hoja. En este caso nos quedan dos rectángulos iguales.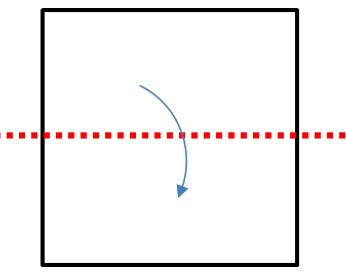
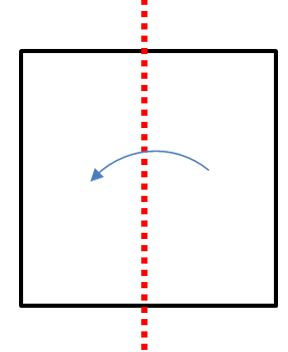Eje 4: Punto medio de los lados – 2
Ahora haz el doblez de os puntos medios pero tomando el eje vertical. Aquí obtienes nuevamente dos rectángulos iguales.>
Tal como pudiste comprobar junto a nosotros, el cuadrado tiene más de un eje de simetría, de hecho tiene 4 ejes de simetría.
Ahora fíjate en esta figura que está dibujada en una hoja de papel:
Vamos a hacer algunos dobleces para encontrar su eje de simetría.
Primero vamos a recortarla por el borde con mucho cuidado.
Ahora vamos a doblarla haciendo que coincidan los bordes de la figura ya recortada.
Nos queda de esta manera.
Y podemos ver que las dos partes son iguales porque se superponen perfectamente.
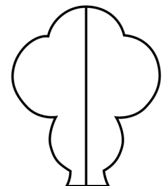Al desdoblar vemos que queda marcado el eje de simetría de la figura.
Figuras sin eje de simetría
Observa la siguiente figura que hemos dibujado en una hoja:
Tratemos de trazar un eje de simetría vertical:
Como puedes ver las dos partes en los que se divide la figura no son iguales. Y lo mismo ocurrirá si seguimos intentándolo con otros ejes.
Entonces esta figura no tiene ejes de simetría. Podemos decir, como ya hemos comentado, que es una figura asimétrica.
Prepara la regla y las tijeras, échale ganas y pon en práctica lo que es un eje de simetría y cómo dar con él o cómo trazarlo.
Tipos de Simetría
En este apartado conoceremos algunos tipos de simetría. Para visualizar mejor estás ideas trabajaremos con doblez de papel, por lo que necesitaremos hojas y tijeras.
Simetría de Reflexión
Trabajaremos con una hoja de papel de forma rectangular, siguiendo los siguientes pasos:
Doblaremos la hoja de papel por la mitad, obteniendo uno de sus ejes.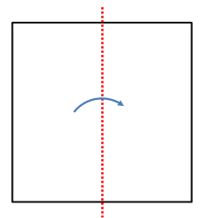
Ahora dibujaremos la figura de nuestra preferencia en una de las caras de la hoja que doblaste.
Recortamos esta figura.
Ahora desdoblamos y destacaremos en ella el eje de simetría. De este modo obtenemos nuestra Simetría de Reflexión.
La Simetría de Reflexión es la correspondencia exacta de las partes de la figura en cuanto a tamaño, forma y posición con relación al eje de simetría.
Simetría de Traslación
Para este caso necesitamos tener a la mano un trozo de papel rectangular.
Doblamos la hoja a la mitad. Luego volvemos a doblar a la mitad considerando el mismo sentido.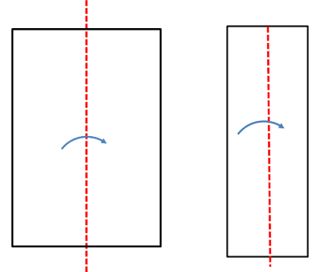
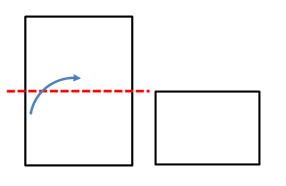Ahora en sentido contrario doblamos a la mitad y después otra vez a la mitad.
Es el momento de dibujar una figura que en algunos de sus puntos toque los dos bordes verticales. Seguidamente recortamos por el borde de los triángulos.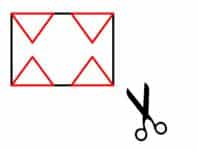
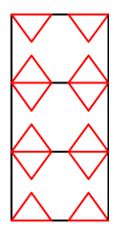Obtenemos la siguiente imagen que representa una simetría de traslación.
La Simetría de Traslación es aquella en la que un diseño se mueve de un lado a otro. La misma imagen se encuentra en otro lugar con la misma orientación.
Simetría de Rotación
Para estudiar este tipo de simetría necesitamos una hoja de papel cuadrada, puede ser de 10 cm x 10 cm o 20 cm x 20 cm.
Doblaremos el cuadrado considerando un eje de simetría vertical.
Ahora haremos un segundo doblez considerando un eje de simetría horizontal.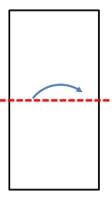
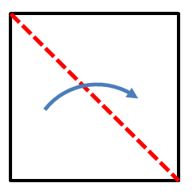Del paso anterior se obtiene un cuadrado que a continuación doblaremos por la diagonal
En el triángulo que obtuvimos trazaremos un cuadrado que no toque los vértices.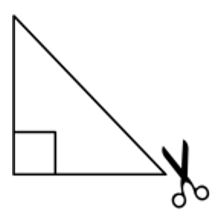
Recortamos el cuadrado y obtenemos esta imagen en la que queda determinada una simetría de rotación.
Una o varias figuras presentan Simetría Rotacional cuando no cambian al ser giradas en un cierto ángulo.
Llega el turno de discriminar y trazar los distintos tipos de ejes de simetría. Para ello, te ofrecemos los siguientes recursos:
La simetría en nuestro alrededor
En esta sección mostraremos diferentes aspectos en nuestra vida en a que se aprecia la simetría y su belleza.
Simetría en las letras
A varias letras mayúsculas del abecedario podemos encontrarles uno o más ejes de simetría. Veamos algunos ejemplos:
La letra A tiene 1 eje de simetría.
La letra B tiene 1 eje de simetría.
La letra H tiene 2 ejes de simetría.
Simetría en el arte
En muchas obras de arte emplean la simetría para armonizar sus elementos y hacerlas ver mucho más bellas.
El famoso artista Escher usa la simetría para hacer los llamados teselados en sus obras:
Aquí te presentamos algunas composiciones artísticas hechas a partir de la simetría:
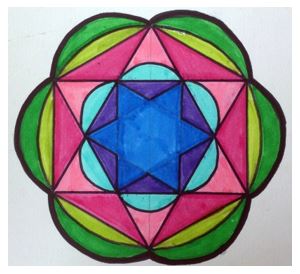Esta composición admite varios ejes de simetría.
¡Trata de ver cuántos ejes puedes trazar!
Esta otra composición se realizó usando simetría de reflexión y de rotación. ¡Está genial!
Simetría en la naturaleza
Según Galileo Galilei, “Dios escribió el universo en el lenguaje de la Matemática”.
Y, tal como podemos observar en las siguientes imágenes, en el lenguaje de la simetría se pueden apreciar bellos ejemplos de ello.
Aquí presentamos varias imágenes de la naturaleza donde se evidencian distintos tipos de simetría:
Simetría en la Matemática
Un triángulo muy famoso en Matemática es el triángulo de Pascal o Tartaglia, también conocido como triángulo de Yanghui.
Este triángulo presenta un caso hermoso de simetría. Obsérvalo:
Antes de dar por terminado el texto no te quedes con las ganas de descubrir las simetrías que nos rodean y reflexionar sobre cómo estamos rodeados de Matemáticas.
Selecciona un juego 👇 👇 👇
Ejes de simetría 1
Ejes de simetría 2
Ejes de simetría 3
Ejes de simetría 4
Ejes de simetría 5
Ejes de simetría 6
Cuestionario
Registrado en SafeCreative.
Mª Gabriela Gracia y Darwin Silva
Profesores universitarios. Magísters en Educación Mención Enseñanza de la Matemática. Investigadores en el área de innovaciones educativas.
Registrado en SafeCreative.