Comparación de números naturales
Muchas veces tenemos que contar, enumerar e incluso ordenar objetos en nuestra vida diaria. Por ello, es muy importante saber cómo realizar la comparación de números naturales para realizar todas estas tareas de forma sencilla y efectiva.

En este artículo aprenderás, cómo hacer la comparación de números naturales, verás ejemplos de mayor que y menor que, el signo mayor o igual y ejercicios de comparación de números.
¿Cómo hacer la comparación de números naturales?
Para comparar números naturales debemos fijarnos en sus cifras y el orden al que llega cada número, sean decenas, centenas, miles o millones.
Estos son los pasos que debes seguir al hacer la comparación de números naturales:
- Fíjate en el orden al que llegan las cifras de los números. El que llegue al orden superior será el mayor.
- Por ejemplo:
- ¿Quién es el número mayor entre 1.562 y 759?
- Vamos a representar ambos números en el cartel de valor para que sea sencillo hacer la comparación:
| Unidad de millar | Centena | Decena | Unidad |
| 1 | 5 | 6 | 2 |
| 7 | 5 | 9 |
- En este caso, 1.562 es mayor que 759 porque 1.562 llega a las unidades de mil, mientras que 759 llega al orden de las centenas, y los miles son mayores que las centenas.
- Si ambos números llegan al mismo orden, compara cada cifra para determinar cuál es el mayor. Al llegar a la cifra que tengan distinta el mayor será el que tenga la cifra de mayor valor.
- Por ejemplo:
- ¿Será cierto que 2.146 es mayor que 3.423?
| Unidad de millar | Centena | Decena | Unidad |
| 2 | 1 | 4 | 6 |
| 3 | 4 | 2 | 3 |
- Al observar estos números vemos que ambos llegan a la unidad de mil.
- Sin embargo, cómo 2 es menor que 3 decimos que 2.146 es menor que 3.426.
- Por tanto, no es cierto que 2.146 es mayor que 3.426
- Observa este otro ejemplo.
- ¿Es 5.985 mayor o menor que 5.972?
| Unidad de millar | Centena | Decena | Unidad |
| 5 | 9 | 8 | 5 |
| 5 | 9 | 7 | 2 |
- Como puedes ver, ambos números llegan a la unidad de mil. Y la cifra que ocupa ese orden es igual a 5 en los dos números.
- Debemos fijarnos entonces en las centenas de los dos números. Al observar, notamos que ambos números tienen la cifra 9 en el orden de las centenas.
- Pasamos entonces al orden de las decenas. Y, como puedes darte cuenta, 8 > 7.
- Por lo tanto, 5.985 es mayor que 5.972.
Ejemplos de mayor que y menor que
En este apartado tienes ejemplos de mayor que y menor que. Estos ejemplos te ayudarán a aclarar aún más cómo se hace la comparación de números en diferentes contextos.
- Ejemplo 1
- ¿Qué número es mayor entre 29.563 y 29.365?
- Respuesta:
- Usemos el cartel de valor para representar ambos números.
| Decena de millar | Unidad de millar | Centena | Decena | Unidad |
| 2 | 9 | 5 | 6 | 3 |
| 2 | 9 | 3 | 6 | 5 |
- Al observar los números podemos notar que:
- Estos dos números llegan hasta la decena de mil.
- Ambos tienen las cifras iguales hasta la centena.
- Cuando comparamos las centenas nos damos cuenta que 5 es mayor que 3.
- Por lo tanto, 29.563 es mayor que 29.365.
- Ejemplo 2:
- Observa las cifras que se te presentan a continuación:
5 – 7 – 1 – 0
- Usando todas las cifras que están en el recuadro forma los números que se te indican a continuación:
- Dos números menores que 7.510
- Dos número mayores que 7.045
- Respuesta:
- Para conseguir los números que nos piden nos apoyaremos en la idea de valor de posición. Empezamos con los dos menores:
- En este caso vemos que el número 7.510 tiene las mismas cifras del recuadro. Entonces podemos mover de lugar alguna de las cifras para que el número resultante sea menor.
| Unidad de millar | Centena | Decena | Unidad | |
| Número original | 7 | 5 | 1 | 0 |
| Número resultante 1 | 5 | 7 | 1 | 0 |
| Número resultante 2 | 7 | 5 | 0 | 1 |
- Para obtener el número 5.710 movimos la cifra 7 que estaba en el orden de los miles al orden de las centenas para que perdiera valor. Pasó de valer 7.000 a valer 700. Y la cifra 5 la movimos al orden de las unidades de mil. Y aunque ahora vale 5.000 es menor que 7.000.
- Como ves, 5.710 es menor que 7.510
- Para conseguir el número 7.501 movimos la cifra 1 que estaba en el orden de las decenas al orden de las unidades. Pasó de valer 10 a valer 1. Mientras que la cifra cero pasó al orden de las decenas.
- Como puedes observar, 7.501 es menor que 7.510
- Para conseguir el número 7.501 movimos la cifra 1 que estaba en el orden de las decenas al orden de las unidades. Pasó de valer 10 a valer 1. Mientras que la cifra cero pasó al orden de las decenas.
- El número 7.045 no tiene todas las cifras que están en el recuadro por lo que cambiar de posición sus cifras no es lo que debemos hacer.
- Entonces vamos a construir los dos números mayores a 7.045 empleando las cifras del recuadro.
5 – 7 – 1 – 0
- Nos apoyaremos en el cartel de valor para hacerlo:
| Unidad de millar | Centena | Decena | Unidad | |
| Número original | 7 | 0 | 4 | 5 |
| Número resultante 1 | 7 | 5 | 1 | 0 |
| Número resultante 2 | 7 | 1 | 0 | 5 |
- El número 7.510 es mayor que 7.045 porque 5 es mayor que 0.
- El número 7.105 es mayor que 7.045 porque 1 es mayor que 0.
- Ejemplo 3:
- La mamá de Simón ha estado ahorrando este año para hacer unos arreglos en la casa. Ella lleva ahorrados 5.263 euros y los arreglos salen por un total de 5.063 euros. ¿Lo que tiene hasta ahora le alcanza para hacer los arreglos? ¿Le sobra dinero?¿Por qué?
- Respuesta:
- Para poder resolver este problema vamos a usar la comparación de números naturales.
- Debemos comparar la cantidad que tiene ahorrada la mamá de Simón con la cantidad que necesita para hacer los arreglos de la casa.
| Unidad de millar | Centena | Decena | Unidad | |
| Cantidad ahorrada | 5 | 2 | 6 | 3 |
| Cantidad que necesita | 5 | 0 | 6 | 3 |
- Como puedes observar, 5.263 es mayor que 5.063, porque 2 es mayor que 0.
- Esto quiere decir que lo que tiene ahorrado la mamá de Simón sí le alcanza para realizar los arreglos a la casa.
- Incluso podemos decir que le sobra dinero porque la cantidad que tiene ahorrada es mayor a la cantidad que necesita.
Signo mayor que o menor que
Al comparar los naturales nos damos cuenta que hay números que son mayores o menores que otros, a esta propiedad se le llama relación de orden.
Para expresar por escrito que un número es mayor que otro se acostumbra a utilizar el símbolo mayor que (>), teniendo en cuenta que el número mayor se ubica del lado abierto del símbolo y el menor se coloca del otro lado.
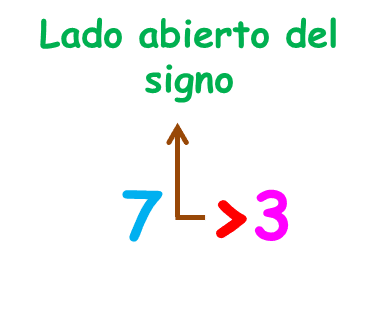 También podemos utilizar el símbolo menor que (<) , para decir que un número es menor que otro. El número menor se ubica al lado del vértice o punta del símbolo menor que (<) y el mayor se coloca del otro lado.
También podemos utilizar el símbolo menor que (<) , para decir que un número es menor que otro. El número menor se ubica al lado del vértice o punta del símbolo menor que (<) y el mayor se coloca del otro lado.

La otra opción que existe al comparar dos números naturales es que los números sean iguales. En este caso utilizamos el signo igual que (=).
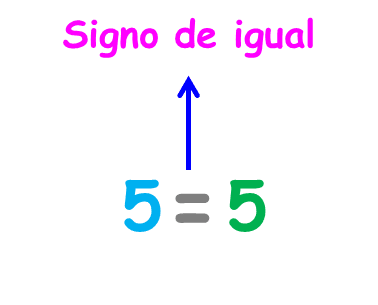
Entonces, dados dos números naturales al compararlos tenemos tres casos que se excluyen mutuamente. Estos son:
| Caso 1 | a > b | a es mayor que b |
| Caso 2 | b < a | b es menor que a |
| Caso 3 | a = b | a es igual a b |
Ejercicios de comparación de números
En este apartado vamos a practicar la comparación de números naturales con algunos ejercicios.
- ¿Qué número es mayor entre 18.635 y 18.139?
- Vamos a representar estos números en el cartel de valor.
| Decena de millar | Unidad de millar | Centena | Decena | Unidad |
| 1 | 8 | 6 | 3 | 5 |
| 1 | 8 | 1 | 3 | 9 |
- Como puedes observar, los dos números alcanzan la decena de mil. La cifra ubicada en ese orden es 1 en ambos números.
- Al ser iguales la cifra de las decenas de mil en ambos números, nos corresponde comparar las unidades de mil.
- Al fijarnos en las unidades de mil nos damos cuenta que ambos números tienen la cifra 8.
- Pasamos entonces al orden de las centenas.
- En 18.635 la cifra que ocupa el lugar de las centenas es 6 y en 18.139 la cifra de la centena es 1 .
- Al comparar ambas cifras podemos ver que 6 > 1 , por esa razón:
18.635 > 18.139
- Ordena de mayor a menor los siguientes números naturales:
12.365 – 8.999 – 3.615 – 8.648 – 365.265 – 12.421 – 3.645 – 365.784
- Lo primero que haremos será identificar cuáles son los órdenes a los que llegan cada uno de los números. Para ello los representaremos en el cartel de valores. Veamos:
| Centena de millar | Decena de millar | Unidad de millar | Centena | Decena | Unidad |
| 1 | 2 | 3 | 6 | 5 | |
| 8 | 9 | 9 | 9 | ||
| 3 | 6 | 1 | 5 | ||
| 8 | 6 | 4 | 8 | ||
| 3 | 6 | 5 | 2 | 6 | 5 |
| 1 | 2 | 4 | 2 | 1 | |
| 3 | 6 | 4 | 5 | ||
| 3 | 6 | 5 | 7 | 8 | 4 |
- Los números que llegan al orden de la centena de millar son: 365.265–365.784
- Los números que alcanzan al orden de la decena de millar son: 12.366 – 12.421
- Los números que llegan a launidad de millar son: 8.999–3.615 – 8.648 – 3.645
- Comparamos ahora cada orden:
- Como el mayor de los órdenes es el de la centena de millar los números mayores son 365.265y365.784.
- 365.265 y 365.784 tienen las cifras iguales hasta la unidad de millar.
- Cuando comparamos las centenas nos damos cuenta que 7 es mayor que 2.
- Por lo tanto, 365.784 es mayor que 365.265.
- De mayor a menor los números van quedando así:
365.784 – 365.265 – …
- Ahora ordenaremos los números que llegan a la decena de millar.
- 12.366 y12.421tienen las cifras iguales hasta la unidad de millar.
- Al comparar las centenas identificamos que 4 es mayor que 3.
- Por lo tanto, 12.421 es mayor que 12.366.
- De mayor a menor los números van quedando así:
365.784 – 365.265 – 12.421 – 12.366 – …
- Por último, vamos a ordenar los números que llegan a la unidad de millar.
- Esos son 8.999, 3.615, 8.648, 3.645.
- Cuando comparamos las unidades de millar podemos ver que 8 es mayor que 3.
- Esto quiere decir que8.999 y 8.648son mayores que 3.615 y 3.645.
- 8.999 y 8.648tienen las cifras iguales hasta las unidades de millar.
- Al comparar las centenas vemos que 9 es mayor que 6.
- Por lo tanto, 8.999 es mayor que 8.648
- De mayor a menor los números van quedando así:
365.784 – 365.265 – 12.421 – 12.366 – 8.999 – 8.648 – …
- 3.615 y 3.645tienen las cifras iguales hasta las centenas.
- Cuando comparamos las decenas podemos ver que 4 es mayor que 1.
- Por lo tanto, 3.645 es mayor que 3.615
- De mayor a menor los números quedan ordenados así:
365.784 – 365.265 – 12.421 – 12.366 – 8.999 – 8.648 – 3.645 – 3.615
- Juan le dice a Pedro, tengo en euros lo equivalente al mayor número de tres cifras más una unidad. Juan le responde a Pedro, yo tengo en euros lo equivalente al menor número de cuatro cifras. ¿Quién tiene más dinero?
- Veamos cuál de los dos tiene más dinero:
- El mayor número de tres cifras llega al orden de las centenas y en cada orden (unidades, decenas y centenas) tiene la cifra de mayor valor absoluto del Sistema de Numeración Decimal, esa cifra es el 9.
- Vamos a representar este número en el cartel de valor:
| Centena | Decena | Unidad |
| 9 | 9 | 9 |
- Concluimos, que el mayor número de tres cifras es el 999. Al sumarle una unidad a 999 el resultado es 1.000.
- Entonces, Juan tiene 1.000 euros.
- Ahora veamos cuánto dinero tiene Pedro.
- El menor número de cuatro cifras es uno que alcanza el orden de las unidades de millar y que en cada orden, excepto en las unidades de mil, tiene la cifra de menor valor absoluto, esa cifra es el 0.
- En el orden de las unidades de millar no puede colocarse el 0, porque de hacerlo el número que se obtendría sería de 0000, ya que como dijimos anteriormente en los otros tres órdenes (centenas, decenas y unidades) colocaremos el cero (0).
- La cifra que colocaremos en el orden de las unidades mil será el 1, que es la cifra no nula de menor valor absoluto.
- Representemos entonces el menor número de cuatro cifras en el cartel de valor.
| Unidad de millar | Centena | Decena | Unidad |
| 1 | 0 | 0 | 0 |
- Concluimos que Pedro tiene 1.000 euros.
- En definitiva, Juan y Pedro tienen cada uno 1.000 euros. Lo que significa que ambos tienen la misma cantidad de dinero.
Antes de terminar, te proponemos unas actividades para que afiances todo lo que has leído sobre la comparación de números naturales.
Selecciona un juego 👇 👇 👇

Comparación Núm. naturales 1

Comparación Núm. naturales 2

Comparación Núm. naturales 3

Comparación Núm. naturales 4

Cuestionario

Comparación Núm. naturales 1

Comparación Núm. naturales 2

Comparación Núm. naturales 3

Comparación Núm. naturales 4

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.

