Comparación de números decimales
Comparar números decimales es algo que hacemos casi a diario. Cuando vamos al mercado, en el centro comercial, en la escuela, y hasta en el hogar, realizamos actividades que requieren establecer qué número es mayor, cuál es menor o cuál es la diferencia que existe entre dos números decimales.

En este artículo te enseñamos cuáles son los números decimales, te explicamos cómo saber qué número decimal es mayor, y te presentamos varios ejercicios resueltos sobre la comparación de números decimales.
¿Cuáles son los números decimales?
Los números decimales son todos los números que conoces. Es decir, 20, 38, 51, 33,… son números decimales. También lo son 19,3; 15,8; 63,1; 36,8;…
Los números que se escriben con las cifras 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, y que además cumplen con los criterios de la base 10 y el valor de posición son números decimales.
Por ejemplo, 4 y 3,25 son números decimales, con la particularidad de que la parte decimal de 4 es igual a cero (0), mientras que la parte decimal de 3,25 es 25 centésimas.

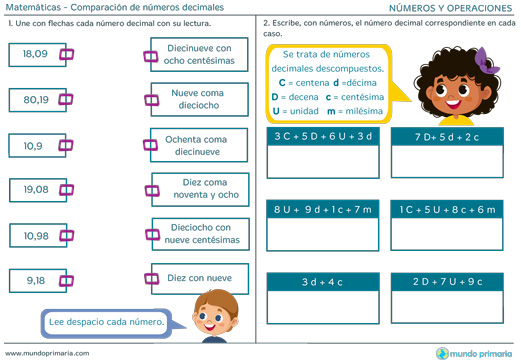
Gracias a las siguientes fichas podrás trabajar con el conjunto de los números decimales antes de pasar a compararlos.
¿Cómo saber qué número decimal es mayor?
En este apartado te explicamos cómo saber qué número decimal es mayor.
A la hora de comparar números decimales es importante que tengas en cuenta los siguientes pasos:
- Paso 1: De ser necesario, iguala con ceros las cifras decimales para que cada número tenga la misma cantidad de cifras en la parte decimal.
- Por ejemplo:
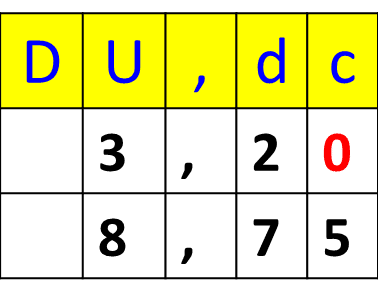
- Si los números que vamos a comparar son 3,2 y 8,75, entonces igualamos la cantidad de cifras decimales en ambos números colocando un cero en el orden de las centésimas del número 3,2.
- Paso 2: Compara la parte entera.
- Caso 1 – La parte entera es diferente: En este caso el número mayor es el que tiene la mayor parte entera.
- Caso 2 – La parte entera es igual: Comparamos orden a orden la parte decimal hasta encontrar la cifra decimal de mayor valor absoluto.
Veamos esto con algunos ejemplos.
Caso 1 – La parte entera es diferente
- Comparemos 4,25 y 1,89.
- La parte entera de 4,25 es diferente a la de 1,89. Y como ves, 4 > 1 por lo que el número mayor es 4,25.
Caso 2 – La parte entera es igual
- Comparemos 15,26 y 15,21.
- La parte entera de 15,26 y 15,21 es 15. Como es igual para ambos números tenemos que pasar a comparar la parte decimal.
- Veamos las cifras de las décimas de 15,26 y 15,21.
- Observa que en ambos casos es 2, por lo que aún no podemos decidir qué número es mayor.
- Tenemos que comparar las cifras de las centésimas de 15,26 y 15,21.
- Como vemos la cifra en el orden de las centésimas de 15,26 es 6 y en 15,21 es 1, como 6 > 1, entonces 15,26 > 15,21.
- Es decir, quince unidades con veintiséis centésimas es mayor que quince unidades con veintiún centésimas.
¿Te ha quedado claro cómo comparar números decimales?
Realicemos un ejemplo más para que no queden dudas.
- Comparemos los números 78,15 y 78,28 para saber cuál es mayor.
- La parte entera de 78,15 y 78,28 es 78, como es igual en ambos números, esto no nos permite decidir cuál es el mayor.
- Tenemos que comparar la cifra de las décimas de ambos números.
- La cifra de las décimas en 78,15 es 1 y en 78,28 es 2.
- Como 2 > 1, entonces 78,28 > 78,15.
Ejemplos de comparación de números decimales
En este apartado verás varios ejemplos de comparación de números decimales que te permitirán comprender mejor cómo hacerlo fácilmente.
- Ejemplo 1: ¿Qué número es menor entre 5,252 y 5,251?
Respuesta:
| En este caso la parte entera es igual en ambos números. | |
| 5,252 | 5,251 |
| Pasamos a las décimas y centésimas. Y vemos que son iguales. | |
| 5,252 | 5,251 |
| Ahora nos fijamos en las milésimas. | |
| 5,252 | 5,251 |
| En este caso. al compararlas tenemos que 2 > 1. Por tanto: | |
| 5,252 > 5,251 | |
| Esto se lee 5,252 es mayor que 5,251 | |
- Ejemplo 2: ¿Es 0,985 menor que 0,99?
Respuesta:
| Al igual que el ejemplo anterior la parte entera es igual en ambos números. | |
| 0,985 | 0,99 |
| Ahora nos fijamos en las décimas, que en este caso son iguales. | |
| 0,985 | 0,99 |
| Vamos a revisar las centésimas. | |
| 0,985 | 0,99 |
| Como ves 8 < 9. Esto quiere decir que: | |
| 0,985 < 0,99 | |
| Esto se lee 0,985 es menor que 0,99 | |
Importante
| Aunque la parte decimal de este número, 985 pareciera mayor que 99, debes fijarte en esto: | |
| 0,985 | 0,99 = 0,990 |
| (Al agregar ceros a la derecha en la parte decimal, el número queda igual) | |
| Esto se lee 985 milésimas | Esto se lee 990 milésimas |
| Entonces 0,985 es menor que 0,990. Por tanto: | |
| 0,985 < 0,99 | |
- Ejemplo 3: ¿Qué número es mayor entre 1,31 y 1,5?
Respuesta:
| Aquí vemos que la parte entera es igual a 1 en los dos números: | |
| 1,31 | 1,5 |
| Ahora comparamos la parte decimal. En este caso, al igual que en el ejemplo anterior, vamos a completar con ceros a la derecha de la parte decimal en el número 1.5. Esto nos permitirá comparar centésimas con centésimas. Nos queda así: | |
| 1,31 | 1,50 |
| Entonces, como 50>31, podemos decir que: | |
| 1,50 > 1,31 | |
| Esto se lee 1,50 es mayor que 1,31 | |
Ejercicios resueltos sobre cómo ordenar números decimales
En este apartado aprenderás a ordenar números decimales, de menor a mayor y de mayor a menor, con ejemplos resueltos paso a paso.
- Ejemplo 1:
- Ordena de mayor a menor los siguientes números:
5,3 – 3,08 – 0,02 – 0,40 – 0,82 – 5,07 – 5,4
- Respuesta:
- Lo primero que hacemos es fijarnos en la parte entera de cada número, y los reagrupamos de mayor a menor.
5,3 – 5,07 – 5,4 – 3,08 – 0,02 – 0,40 – 0,82
- Como ves hay tres números que tienen 5 en la parte entera, un número que tiene 3 en la parte entera y tres números que tienen 0 en la parte entera.
- Vamos a compararlos por grupos para ir ordenándolos tal y como van a quedar.
- Empezamos por los números que tienen 5 en la parte entera. Debemos fijarnos en la parte decimal, específicamente en las décimas.
5,4 >5,3 >5,07
- Luego de ellos vendría el número 3,08. Nos va quedando así:
5,4 > 5,3 > 5,07 > 3,08
- Ahora vamos a comparar los números enteros que tienen 0 en la parte entera. Nos fijamos en la parte decimal, específicamente en las décimas. Tenemos:
0,82 > 0,40 > 0,02
- Por último los colocamos todos juntos en orden:
5,4 > 5,3 > 5,07 > 3,08 > 0,82 > 0,40 > 0,02
- Ejemplo 2:
- Ordena de menor a mayor los siguientes números:
3,710 – 3,16 – 2,18 – 3,019 – 6,072 – 3,190 – 6,206
- Respuesta:
- Nos fijamos primero en la parte entera de cada número y los reagrupamos de menor a mayor.
2,18 – 3,710 – 3,16 – 3,019 – 3,190 – 6,072 – 6,206
- Ahora vamos a ir comparándolos por grupos.
- Empezamos por los que tienen el 3 en la parte entera. Para compararlos nos fijamos en la parte decimal, específicamente en las milésimas, y luego los ordenamos.
- Sabemos que 19 < 160 < 190 < 710
- Nos quedan así:
3,019 < 3,160 < 3,190 < 3,710
- Ahora comparamos los números que tienen 6 en la parte entera. Específicamente nos fijamos en las milésimas.
- Sabemos que 72 < 206
- Tenemos entonces que:
6,072 < 6,206
- Por último, los escribimos todos en orden:
2,18 < 3,019 < 3,160 < 3,190 < 3,710 < 6,072 < 6,206
Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido.
Selecciona un juego 👇 👇 👇

Comparación Núm. decimales - 1

Comparación Núm. decimales - 2

Comparación Núm. decimales - 3

Comparación Núm. decimales - 4

Cuestionario

Comparación Núm. decimales - 1

Comparación Núm. decimales - 2

Comparación Núm. decimales - 3

Comparación Núm. decimales - 4

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.