Círculo y circunferencia
En ocasiones tendemos a pensar que un círculo y una circunferencia es lo mismo, pero no es así. Te animamos a que sigas leyendo y descubras en qué se diferencian uno de la otra y, además, aprendas muchas más cosas como calcular su longitud o su área en el caso de los círculos.
La circunferencia
La circunferencia es un objeto geométrico muy importante, son muchas las aplicaciones que se le han dado a esta curva cerrada que posee una propiedad especial. Veamos de qué se trata.
Definición de circunferencia:

Definición de círculo:
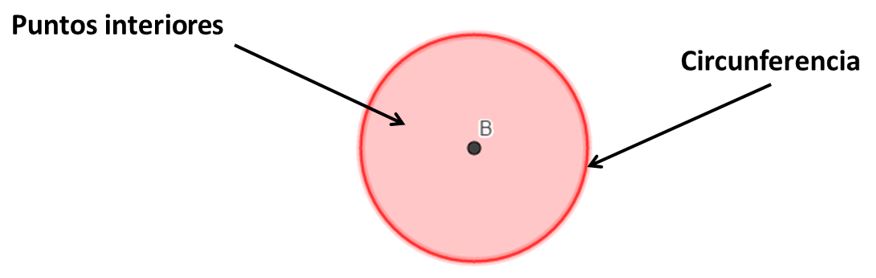
Diferencias entre circunferencia y círculo
La circunferencia y el círculo se diferencian en varios aspectos, y es importante tener estas diferencias en cuenta porque pueden ser muy útiles a la hora de resolver problemas o matematizar situaciones de la vida cotidiana. Observa que:
| CIRCUNFERENCIA | CÍRCULO |
|
|
Algunas aplicaciones del círculo y la circunferencia
Las ideas de circunferencia y círculo han sido utilizadas en una gran cantidad de obras artísticas, tecnológicas y científicas. A continuación te presentamos dos ejemplos en los que se han utilizado estas potentes ideas geométricas.
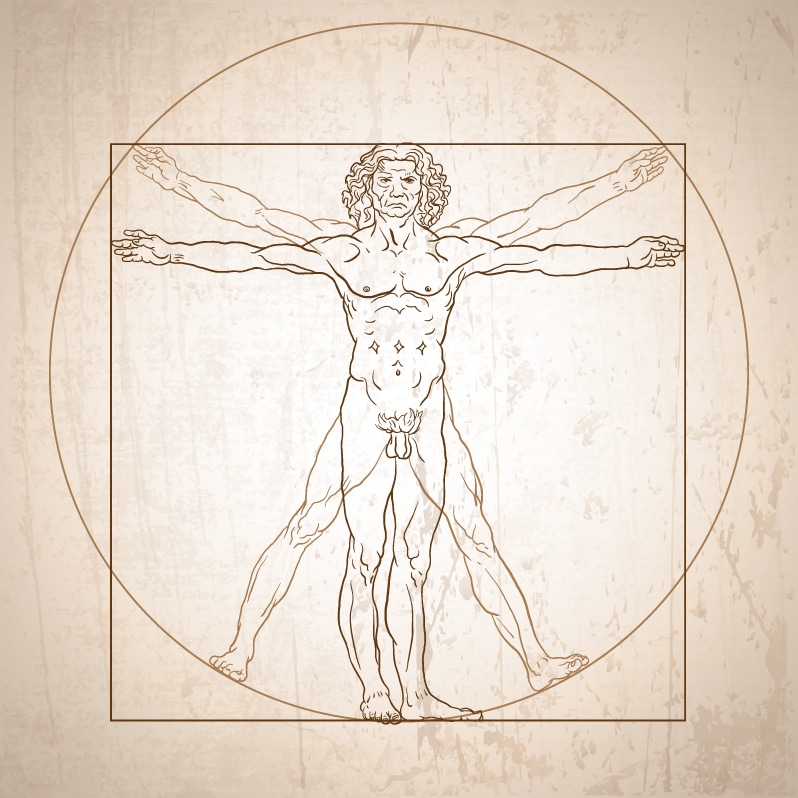
- El Hombre de Vitruvio es una famosa obra de Leonardo da Vinci elaborada alrededor del año 1490. En la imagen se observa una figura masculina en dos posiciones de brazos y piernas e inscrita en una circunferencia y un cuadrado. Se trata de un estudio de las proporciones del cuerpo humano.
- Algunas de las proporciones descritas en el Hombre de Vitruvio son:
- El rostro desde la barbilla hasta la parte más alta de la frente, donde comienzan las raíces del cabello, mide una décima parte de la altura total.
- El pie equivale a una sexta parte de la altura del cuerpo.
- La frente mide la tercera parte del rostro.
- Te invitamos a que verifiques estos datos midiendo tu propio cuerpo. Esperamos haber despertado tu curiosidad y que ahora vayas detrás de la pista otras proporciones delas que habla el Hombre de Vitruvio.
- La Rueda es uno de los inventos más importante de la historia de la humanidad y en ella está presenta la idea de círculo y circunferencia. Ha sido de gran utilidad en la elaboración de alfarería y también en el transporte terrestre. La mayoría de los estudios arqueológicos coinciden en que la rueda fue inventada hacia los años 4500 a.C en Mesopotamia.

- La idea de la circunferencia y el círculo también ha sido utilizada en la arquitectura y la ecología. En la imagen observamos unos inmensos jardines circulares con una única vía para acceder a su interior. Estos jardines están ubicados en Copenhague, la capital de Dinamarca. Son urbanizaciones en las que los vecinos pueden encontrarse en el centro del jardín, porque suelen aparcar ahí sus automóviles.

El número Pi (π), la circunferencia y el círculo
El número pi (π) es la relación que existe entre la longitud de la circunferencia y su diámetro. Es una constante muy importante en matemática, además de ser un número irracional.
El valor numérico de pi (π) con seis cifras decimales es el siguiente:
![]()
Generalmente a la hora de resolver ejercicios y problemas que involucren el número pi (π) se utiliza el valor 3,14.
Deducción del valor del número pi (π)
Para deducir el valor de pi (π) trabajaremos con los siguientes objetos: un vaso, un CD y una lata.

Mediremos en centímetros la longitud de la circunferencia que forma el borde de cada uno de los objetos. Lo realizaremos colocando hilo en el borde del vaso, el CD, y la lata. Luego cortaremos y mediremos la longitud de cada una de las circunferencias formadas por el borde de los objetos.

Escribimos en la siguiente tabla los datos obtenidos al medir la longitud de la circunferencia de los objetos. Es bueno recordar que estos datos son aproximados, la medición siempre tendrá un margen de error.
| OBJETO | LONGITUD DE LA CIRCUNFERENCIA (Lc) | LONGITUD DE DIÁMETRO (LD) | LcLd |
| LATA | 32 cm. | ||
| CD | 39 cm. | ||
| VASO | 23,5 cm. |
Ahora medimos la longitud del diámetro de cada uno de los objetos.

A continuación completamos la columna de la longitud del diámetro con los datos obtenidos a partir de la medición realizada.
| OBJETO | LONGITUD DE LA CIRCUNFERENCIA (Lc) | LONGITUD DE DIÁMETRO (LD) | LcLd |
| LATA | 32 cm. | 10,1 cm | |
| CD | 39 cm. | 12,3 cm. | |
| VASO | 23,5 cm. | 7,4 cm. |
Por último, dividimos la longitud de la circunferencia entre la longitud del diámetro y completamos la tabla.
| OBJETO | LONGITUD DE LA CIRCUNFERENCIA (Lc) | LONGITUD DE DIÁMETRO (LD) | LcLd |
| LATA | 32 cm. | 10,1 cm. | 3,168 |
| CD | 39 cm. | 12,3 cm. | 3,17 |
| VASO | 23,5 cm. | 7,4 cm. | 3,175 |
Al observar los cocientes obtenidos en la última columna nos damos cuenta que todos los valores obtenidos son muy cercanos a 3,14. Si hubiésemos utilizado instrumentos de mayor precisión, como lo son el vernier y el curvímetro, el valor hubiese sido el mismo en todos los casos. Es decir, el resultado obtenido sería una cantidad constante, mucho más próxima a la cantidad denominada pi (π).
Longitud de una circunferencia
Para deducir cómo se calcula la longitud de una circunferencia utilizaremos la tabla del ejemplo anterior.
| OBJETO | LONGITUD DE LA CIRCUNFERENCIA (Lc) | LONGITUD DE DIÁMETRO (LD) | LcLd |
| LATA | 32 cm. | 10,1 cm. | 3,168 |
| CD | 39 cm. | 12,3 cm. | 3,17 |
| VASO | 23,5 cm. | 7,4 cm. | 3,175 |
A la última columna le cambiaremos el nombre, ahora la llamaremos π1. Esto lo hacemos debido a que como ya vimos los resultados obtenidos al dividir la longitud de la circunferencia entre la longitud del diámetro se aproximan bastante al valor de pi (π).
| OBJETO | LONGITUD DE LA CIRCUNFERENCIA (Lc) | LONGITUD DE DIÁMETRO (LD) | π1 |
| LATA | 32 cm. | 10,1 cm. | 3,168 |
| CD | 39 cm. | 12,3 cm. | 3,17 |
| VASO | 23,5 cm. | 7,4 cm. | 3,175 |
Ahora veamos qué operación podemos aplicar con los valores de las dos últimas columnas para que obtengamos la longitud de la circunferencia.
- Analicemos los valores obtenidos con la lata:
| OBJETO | LONGITUD DE LA CIRCUNFERENCIA (Lc) | LONGITUD DE DIÁMETRO (LD) | π1 |
| LATA | 32 cm. | 10,1 cm. | 3,168 |
- Si sumamos 10,1 más 3,168 (Ld + π1) se obtiene 13,268, este resultado no es igual al valor de la longitud de la circunferencia de la lata. Por esta razón, la adición no es la operación que nos permite combinar los resultados de las últimas dos columnas para obtenerla longitud de la circunferencia.
- Al restar 10,1 con 3,168 (Ld – π1 ) la diferencia es 6,932, tampoco se obtiene el valor de la longitud de la circunferencia de la lata.
- Cuando multiplicamos 10,1 por 3,168 (Ld x π1) el resultado es 31,9968 si redondeamos a la unidad más cercana el resultado es 32. En este caso sí obtenemos la longitud de la circunferencia de la lata.
- Entonces, si multiplicamos la longitud del diámetro por el valor de pi (π) el resultado es igual a la longitud de la circunferencia de la lata.
Veamos si esta conjetura es cierta para los casos de la longitud de la circunferencia del CD y la del vaso:
| OBJETO | LONGITUD DE LA CIRCUNFERENCIA (Lc) | LONGITUD DE DIÁMETRO (LD) | π1 |
| LATA | 32 cm. | 10,1 cm. | 3,168 |
| CD | 39 cm. | 12,3 cm. | 3,17 |
- Probemos primero con el CD:
- Al multiplicar 12,3 por 3,17 (Ld x π1) el resultado es 38,991 si aproximamos este número a la unidad más cercana obtenemos 39, que es la longitud de la circunferencia del CD. En este caso, también se cumple que la longitud de la circunferencia del CD se obtiene multiplicando la longitud del diámetro por un valor aproximado de pi (π).
- Veamos que sucede con el vaso:
- Si multiplicamos 7,4 por 3,175 (Ld x π1) el resultado es 23,495, aproximando a la décima más cercana se obtiene 23,5. En este caso también se cumple que la longitud de la circunferencia del vaso es igual a la longitud del diámetro multiplicada por el valor de pi (π).
Fórmula de la longitud de una circunferencia
Efectivamente, tal y como hemos visto en cada uno de los casos anteriores la longitud de una circunferencia se define como la multiplicación de la longitud del diámetro por el valor de pi (π).
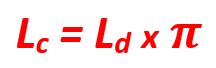
- Lc: Longitud de la circunferencia.
- Ld: Longitud del diámetro.
- π: Valor de pi.
Problemas de longitud de una circunferencia
- Problema 1:
- La rueda de una camioneta tiene 85cm de radio. ¿Cuánto ha recorrido la camioneta cuando la rueda ha dado 65 vueltas?
- Para responder a la interrogante lo primero que debemos saber es cuál es la longitud de la circunferencia de la rueda de la camioneta. Para conocer este dato utilizaremos la ecuación de la longitud de la circunferencia que acabamos de deducir.
- La rueda de una camioneta tiene 85cm de radio. ¿Cuánto ha recorrido la camioneta cuando la rueda ha dado 65 vueltas?
| OPERACIÓN | EXPLICACIÓN |
| Lc = Ld x π | Ecuación para calcular la longitud de una circunferencia. |
| Lc = 170 cm x π | Calculamos el valor de la longitud del diámetro que es igual a dos veces la longitud del radio. Esto es, Ld = 2 x 85 cm = 170 cm. |
| Lc = 170cm x 3,14 | Utilizamos como valor aproximado de π el 3,14 y lo sustituimos en la ecuación. |
| Lc = 533,8 cm | Multiplicamos la longitud del diámetro por el valor de π. |
- Ya sabemos que la longitud de la rueda de la circunferencia es 533,8 cm. Ahora para determinar cuánto ha recorrido la rueda al dar 65 vueltas, multiplicamos la longitud de la circunferencia de la rueda por 65. Esto es;
- 65 x 533,8 cm = 34.697 cm
- Entonces la rueda al dar 65 vueltas recorre una distancia de 34.697 cm.
- Problema 2:
- Calcula el radio de una circunferencia de 68, 5 cm de longitud.
- En este problema debemos calcular longitud del radio sabiendo la longitud de la circunferencia. De igual manera utilizaremos la ecuación de la longitud de la circunferencia.
| OPERACIÓN | EXPLICACIÓN |
| Lc = Ld x π | Ecuación para calcular la longitud de una circunferencia. |
| 68,5 cm = Ld x 3,14 | Sustituyendo el valor de la longitud de la circunferencia y el valor de pi en la ecuación. |
| 68,5 cm ÷ 3,14= Ld | Transponiendo el valor de pi al primer miembro de la ecuación. Recuerda que si un término está en uno de los miembros multiplicando lo pasamos al otro miembro dividiendo. |
| Ld = 21,82 cm | Dividiendo 68,5 cm ÷ 3,14. |
| Lr = 21,82 ÷ 2 | La longitud del radio (Lr) es igual a la mitad de la longitud del diámetro. |
| Lr = 10,91 cm | Dividiendo 21,82 cm ÷ 2 |
- El radio de la circunferencia de longitud 68,5 cm es 10,91 cm.
Área de un círculo
Al ser el círculo una figura plana es posible calcular su área. Esta idea es muy importante porque permite resolver una gran cantidad de problemas geométricos.
El área de un círculo es igual al producto de A y el cuadrado del radio del círculo. Esto es:
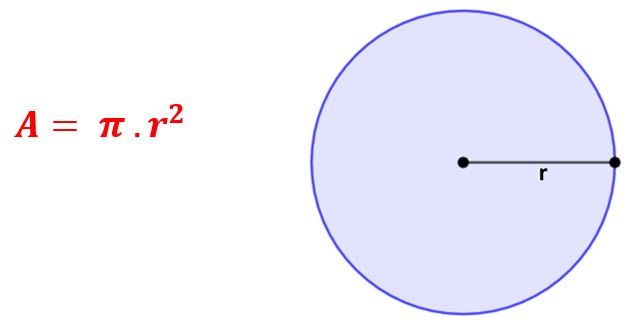
Problemas de área de un círculo
- Problema 1:
- ¿Cuál es el área de un círculo 12 cm de diámetro?
- Para responder a esta pregunta utilizaremos la ecuación del área de un círculo.
- ¿Cuál es el área de un círculo 12 cm de diámetro?
| OPERACIÓN | EXPLICACIÓN |
| A = π x r² | Ecuación para calcular el área de un círculo. |
| A = 3,14 x r² | Sustituyendo el valor de pi en la ecuación. |
| A = 3,14 x (6cm)² | Sustituyendo el valor del radio, que es igual a la mitad del diámetro. Es decir, 12 cm ÷ 2 = 6 cm. |
| A = 3,14 x 36 cm² | Resolviendo la potencia. |
| A = 113,04 cm² | Realizando la multiplicación. |
- Entonces, el área del círculo de diámetro 12 cm es 113,04 cm2.
- Problema 2:
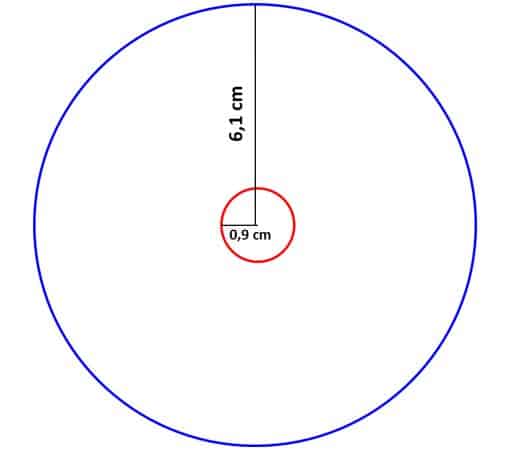
- En un centro de impresiones hacen etiquetas para discos de música de forma que se cubra la parte superior del CD. Si se sabe que el radio mayor mide 6,1 cm y el menor 0,9 cm aproximadamente, ¿cuál es el área que cubre la etiqueta?
- En la imagen tenemos una representación del CD del que se habla en el problema. En este caso para conocer cuál es el área que cubre la etiqueta, calcularemos tanto el área del círculo cuyo radio es 6,1 cm (círculo mayor) como el área del círculo de radio 0,9 cm (círculo menor).
- En un centro de impresiones hacen etiquetas para discos de música de forma que se cubra la parte superior del CD. Si se sabe que el radio mayor mide 6,1 cm y el menor 0,9 cm aproximadamente, ¿cuál es el área que cubre la etiqueta?
- Primero calcularemos el área del círculo mayor (A1).
| OPERACIÓN | EXPLICACIÓN |
| A1 = π x r² | Ecuación para calcular el área de un círculo. |
| A1 = 3,14 x (6,1cm)² | Sustituyendo el valor de pi y el del radio en la ecuación. |
| A1 = 3,14 x 37,21 cm² | Resolviendo la potencia. |
| A1 = 116,84 cm² | Realizando la multiplicación. |
- Ahora calcularemos el área del círculo menor (A2)
| OPERACIÓN | EXPLICACIÓN |
| A2 = π x r² | Ecuación para calcular el área de un círculo. |
| A2 = 3,14 x (0,9cm)² | Sustituyendo el valor de pi y el del radio en la ecuación. |
| A2 = 3,14 x 0,81 cm² | Resolviendo la potencia. |
| A2 = 2,54 cm² | Realizando la multiplicación. |
- A continuación restaremos el área del círculo mayor menos el área del círculo menor. De esta manera sabremos cuál es el Área que cubre la Etiqueta (Ae).
- Ae = A1 – A2 = 116,84 cm2 – 2,54 cm2 = 114,3 cm2.
- De esta manera el área que cubre la etiqueta es 114,3 cm2.
- A continuación restaremos el área del círculo mayor menos el área del círculo menor. De esta manera sabremos cuál es el Área que cubre la Etiqueta (Ae).
Selecciona un juego 👇 👇 👇

Características del círculo y la circunferencia

Diferenciación entre círculos y circunferencias 1

Diferenciación entre círculos y circunferencias 2

Fórmulas del círculo y de la circunferencia

Uso de las fórmulas del círculo y de la circunferencia

Problemas sobre círculos y circunferencias

Cuestionario

Características del círculo y la circunferencia

Diferenciación entre círculos y circunferencias 1

Diferenciación entre círculos y circunferencias 2

Fórmulas del círculo y de la circunferencia

Uso de las fórmulas del círculo y de la circunferencia

Problemas sobre círculos y circunferencias

Cuestionario
![]() Registrado en SafeCreative.
Registrado en SafeCreative.
