Cálculo de porcentajes

El porcentaje es uno de los conceptos de la matemática más utilizados de hecho, casi todas las personas calculan un tanto por ciento por lo menos una vez en su vida.

En muchas ocasiones cuando vamos al mercado, al centro comercial o cuando pagamos la factura eléctrica, aplicamos la idea de porcentaje para calcular un descuento o un impuesto.

 

¿Qué es el porcentaje?

Los porcentajes son una manera de representar las partes de un número entero. Al igual que las fracciones y los números decimales.

Los porcentajes constan de un número acompañado del símbolo %, que se pronuncia “por ciento”, y que significa “por cada 100”.

Al hablar de 55% nos referimos a 55 de cada 100. De igual manera pasa con cualquier otro porcentaje, sea este 10%, 50%, 75%,120% o cualquier otro.

 

El porcentaje como una fracción.

En esta sección te explicamos de qué manera se puede escribir el porcentaje como una fracción. También te decimos cómo ir de una fracción a un porcentaje.

 

De porcentaje a fracción

Cuando nos referimos al 15%, realmente estamos hablando de una fracción cuyo numerador es 15 y el denominador es 100.

15% = ¹⁵₁₀₀

Como ya sabes, si el numerador y el denominador de una fracción tienen divisores comunes diferentes de 1, entonces es posible simplificarla.

En el caso del 15% la simplificación sería la siguiente:

15% =¹⁵₁₀₀ =³₂₀

El 5 es divisor común de 15 y 100.

 

• Veamos cómo se escribe 20%, 73% y 120% en forma de fracción.
• 20% en forma de fracción:

20% = ²⁰₁₀₀ = ⁴₂₀= ¹₅

• • 4 y 5 son los divisores comunes de 20 y 100.

 

• 73% en forma de fracción:

73% = ⁷³₁₀₀

• •  73 y 100 no tienen divisores comunes distintos de 1, por lo que no es posible simplificar esta fracción.

 

• 120% en forma de fracción:

120% = ¹²⁰₁₀₀ = ¹²₁₀= ⁶₅

• •  10 y 2 son divisores comunes de 120 y 100.

 

De fracción a porcentaje

Cuando tenemos una fracción es posible determinar el porcentaje que está asociado a ella. Veamos:

• Si queremos saber cuál es el porcentaje asociado a la fracción  ⁷₂₀ , entonces multiplicamos  el denominador y el numerador por un mismo número de tal modo que obtengamos 100 en el denominador. Esto es:

⁷₂₀= ^{7 x 5}_{20 x 5}= ³⁵₁₀₀= 35%

• •  De esta manera obtenemos que 35% es equivalente a ⁷₂₀

 

• En el caso de la fracción ¹⁷₂₅ multiplicamos el denominador y el numerador por 4, de tal modo que el resultado en el denominador sea 100.

¹⁷₂₅= ^{17 x 4}_{25 x 4}= ²⁸₁₀₀= 68%

• • De acuerdo a los cálculos realizados la fracción ¹⁷₂₅ es equivalente a 68%

 

• Por último, si queremos saber a qué porcentaje es equivalente la fracción ¹⁵₂₅₀ procedemos de la siguiente manera:
  • Como el denominador es mayor que 100 dividimos el numerador y el denominador por 5 que es un divisor común de 15 y 250. Obtenemos lo siguiente:

¹⁵₂₅₀= ^{15 : 5}_{250 : 5}= ³₅₀

• • Ahora multiplicamos el numerador y el denominador por 2, de tal modo que obtengamos 100 en el denominador.

¹⁵₂₅₀=^{15 : 5}_{250 : 5}= ³₅₀= ^{3 x 2}_{50 x 2}= ⁶₁₀₀= 6%

 

Representación gráfica de un porcentaje.

Como ya hemos explicado, un porcentaje es una fracción en la que el denominador es 100. Por ejemplo, si queremos representar gráficamente 12% que es igual a ¹²₁₀₀, entonces dividimos una unidad en 100 partes iguales y seleccionamos 12 de esas partes. Veamos:

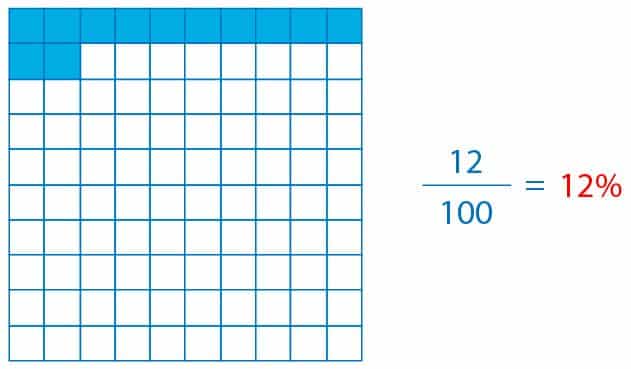
En este gráfico hemos sombreado 12 de las 100 partes en las que ha quedado dividida la unidad. Esta es una manera de visualizar el 12%.

Si ahora queremos visualizar el significado de 100%, realizamos un procedimiento similar al anterior. Dividimos una unidad en 100 partes iguales y en este caso seleccionamos las 100 partes.

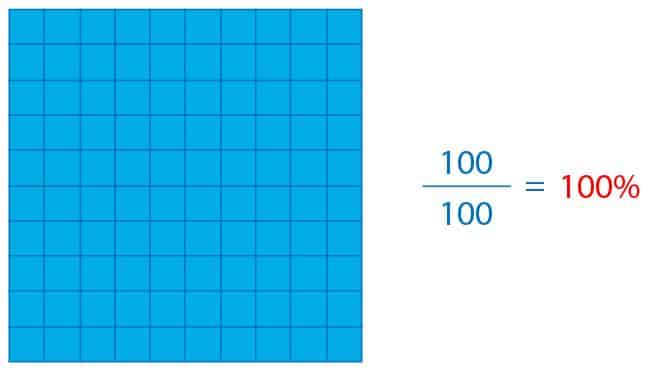
Cuando nos referimos al 100% estamos hablando del todo o totalidad. Por ejemplo, si en una clase hay 25 estudiantes de los cuales 13 son niñas y 12 niños, entonces podemos afirmar que 25 es el 100% de los estudiantes de la clase. Otro caso que es interesante visualizar es cuando los porcentajes son mayores que 100%. Por ejemplo, para representar 120% requerimos más de una unidad. Veamos:

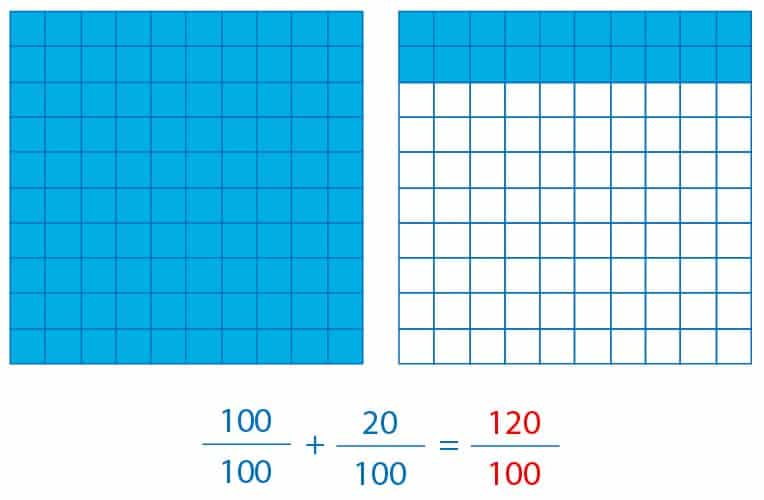
En este caso hemos seleccionado una unidad completa ( ¹⁰⁰₁₀₀) y 20 de las 100 partes ( ²⁰₁₀₀) de otra unidad. Esto quiere decir que ¹²⁰₁₀₀= 120% es más grande que el todo o unidad.

 

Expresión decimal de un porcentaje

Como ya hemos visto el porcentaje es una fracción de denominador igual a 100. Además, sabemos que toda fracción puede expresarse como un número decimal, por lo que el porcentaje puede escribirse en forma de expresión decimal.

Veamos algunos ejemplos:

 

Del porcentaje al decimal

1. Para saber cuál es la expresión decimal asociada a 28% realizamos lo siguiente:

• Primero escribimos el porcentaje, en este caso 28%, como una fracción

28% = ²⁸₁₀₀

• Luego, dividimos el numerador entre el denominador. En este caso sería:

28 : 100 =0,28

28% = ²⁸₁₀₀=0,28

• • De esta manera se obtiene que el decimal asociado a 28% es 0,28 en forma de decimal.

 

2. Si queremos expresar 67% en forma de número decimal, realizamos un proceso similar al anterior.

• Escribimos 67% en forma de fracción:

67% = ⁶⁷₁₀₀

•  Ahora dividimos 67 : 100 = 0,67

67% = ⁶⁷₁₀₀=0,67

• • 67% expresado en forma de decimal es 0,67

 

Del decimal al porcentaje

1.  Para expresar 0,52 en forma de porcentaje, lo primero que debemos hacer es escribir el decimal en forma de fracción. Para ello sigue los siguientes pasos:

• Escribe el número sin la coma en el numerador.
• En el denominador escribe la unidad seguida de tantos ceros como decimales tenga el número. En este caso como son dos decimales, dividimos entre 100. Veamos:

0,52 = ⁵²₁₀₀

•  Luego, aplicamos la definición de porcentaje.

0,52 = ⁵²₁₀₀=52%

 

2. Para escribir 1,25 en forma de porcentaje realizamos un procedimiento similar al anterior.

• Escribimos 1,25 en forma de fracción.

1,25 = ¹²⁵₁₀₀

 

• Luego aplicamos la definición de porcentaje.

1,25 = ¹²⁵₁₀₀=125%

 

 

Cómo calcular el porcentaje que representa una cantidad.

En este apartado te explicamos cómo saber qué porcentaje representa cierta cantidad de otra cantidad que se ha dado.

Es decir, vamos a calcular qué porcentaje representa  de una cantidad  dada.

Para ello debemos seguir tres sencillos pasos:

Paso 1: Representamos en forma de fracción la expresión con la que estamos trabajando.

En este paso simplificamos la fracción, sólo de ser posible.

^x_y

Paso 2: Calculamos la expresión decimal de la fracción obtenida en el paso 1.

Esto es el cociente obtenido al realizar la operación.

x ÷ y

Paso 3: Multiplicamos por 100 la expresión decimal que obtuvimos en el paso 2.

Veamos algunos ejemplos:

 

Ejemplo 1: ¿Qué porcentaje representa 20 de 60?

Paso 1: Escribimos la representación en forma de fracción, y nos queda que 20 de 60 puede expresarse así:

²⁰₆₀= ²₆= ¹₃

Como puedes observar, también hemos simplificado la fracción.

 

Paso 2: Ahora calculamos la expresión decimal de esta fracción. Para ello dividimos el numerador entre el denominador, y nos resulta lo siguiente:

¹₃=1 ÷ 3 = 0,333…

Paso 3: Por último, multiplicamos la expresión decimal de la fracción por 100. Nos queda así:

0,333 x 100 = 33,33%

• Podemos decir que 20 representa el 33,33% de 60.

 

Ejemplo 2: ¿Qué porcentaje es 5 de 25?

Paso 1: Escribimos en forma de fracción la expresión dada, y simplificamos, quedando así:

⁵₂₅ = ¹₅

Paso 2: Calculamos la expresión decimal de la fracción anterior, y tenemos lo siguiente:

¹₅=1 ÷ 5 = 0,2

Paso 3: Multiplicamos la expresión decimal anterior por 100, de esta forma:

0,2 x 100 = 20%

• Nos queda que 5 es el 20% de 25.

 

Ejemplo 3: En la clase de spinning de un gimnasio hay inscritas 36 personas, de las cuales 27 son mujeres. ¿Qué porcentaje representa la cantidad de mujeres del total de inscritos en la clase?

Este es un problema sencillo que podemos resolver calculando qué porcentaje representa 27 (cantidad de mujeres) de 36 (número total de inscritos en la clase).

Paso 1: Empecemos escribiendo la expresión en forma de fracción:

²⁷₃₆ = ³₄

Paso 2: Calculamos la expresión decimal de la fracción, y nos queda:

³₄=3 ÷ 4 = 0,75

Paso 3: Multiplicamos por 100 la expresión decimal, y tenemos:

0,75 x 100 = 75%

• Por ello, las mujeres representan el 75% del total de inscritos a la clase de spinning.

 

Ejemplo 4:En una caja de chocolates hay 50 bombones. De estos 50 bombones 15 están rellenos de cacahuete, y son mis favoritos. ¿Qué porcentaje de bombones no están rellenos de cacahuete del total de bombones de la caja?

Para resolver este problema primero tenemos que calcular exactamente cuántos bombones no están rellenos de cacahuete.

Entonces, restamos los que sí traen maní del total de bombones de la caja:

50 – 15 = 35

Sabemos ahora que hay 35 bombones que no están rellenos de cacahuete.

Ahora veamos qué porcentaje representan estos 35 bombones sin cacahuete del total de 50 bombones de la caja.

Paso 1: Representemos en forma de fracción la expresión anterior y la simplificamos:

³⁵₅₀ = ⁷₁₀

Paso 2: Calculamos la expresión decimal de la fracción:

⁷₁₀=7 ÷ 10 = 0,7

Paso 3: Multiplicamos la expresión decimal que encontramos en el paso anterior por 100:

0,7 x 100 = 70%

• Por último, sabemos que el 70% de los bombones no están rellenos de maní.

 

Calcular el porcentaje de un número.

Para calcular el porcentaje de un número usaremos la expresión fraccionaria del porcentaje que queremos calcular, también usaremos la idea de proporcionalidad y la expresión decimal de porcentaje.

Tenemos entonces estas dos formas de calcular el porcentaje de un número:

Forma 1: Calcularemos el porcentaje de un número con la expresión fraccionaria del porcentaje y la idea de proporcionalidad.

• Por ejemplo, si queremos calcular el 40% de 120 lo primero que hacemos es expresar el porcentaje en forma de fracción, y nos queda:

⁴⁰₁₀₀

• Luego, llamaremos  a la cantidad que representa el porcentaje que queremos calcular y establecemos la misma relación que con las cantidades anteriores:

^x₁₂₀

• Ahora aplicamos la proporcionalidad que existe entre estas dos expresiones, porque 40 es a 100 como  es a 120. Nos queda lo siguiente:

⁴⁰₁₀₀=^x₁₂₀

• De esta expresión obtenemos que:

x = ^{40 x 120}₁₀₀

• Ahora podemos calcular el porcentaje que queremos:

x = ^{40 x 120}₁₀₀

x = ⁴⁸⁰⁰₁₀₀

x = 48

• • Podemos concluir que el 40% de 120 es 48.

Forma 2: Usamos la expresión fraccionaria del porcentaje y la expresión decimal del porcentaje.

• Vamos a trabajar con el mismo caso que empleamos en la forma 1, para que veas que obtendremos el mismo resultado.
• Entonces calcularemos el 40% de 120.
• Lo primero que haremos es expresar el porcentaje que queremos calcular en forma de fracción:

40% = ⁴⁰₁₀₀

• Ahora vamos a calcular la expresión decimal del porcentaje. Para ello dividimos el numerador entre el denominador, y tenemos:

40% = ⁴⁰₁₀₀=0,4

• Ya tenemos la expresión decimal del porcentaje.
• Por último, multiplicamos la cantidad a la que queremos calcular ese porcentaje por la expresión decimal del porcentaje:

120 x 0,4 = 48

• • Concluimos que el 40% de 120 es 48.

 

Vamos a resolver un par de ejercicios para calcular el porcentaje de un número.

Ejercicio 1: Calcula el 35% de 225.

Observa cómo lo calculamos con ambas formas.

Forma 1:

• Expresamos 35% en forma fraccionaria, y aplicamos esa misma relación entre la cantidad que representa el porcentaje que queremos calcular () y la cantidad total a la que queremos calcular ese porcentaje, que en este caso es 225.

³⁵₁₀₀=^x₂₂₅

• Recuerda que 35 es a 100 como x es a 225. De ahí tenemos que:

x =^{35 x 225}₁₀₀

x =^7.825₁₀₀

x = 78,25

• • Entonces, el 35% de 225 es 78,25.

 

Forma 2:

• De igual manera, expresamos 35% en forma de fracción. Luego, calculamos la expresión decimal de ese porcentaje:

³⁵₁₀₀= 0,35

• Ahora, multiplicamos la expresión decimal del porcentaje por la cantidad a la que vamos a calcular el porcentaje:

 

225 x 0,35 = 78,75

• • Al igual que con la forma 1, concluimos que el 35% de 225 es 78,75.

 

Ejercicio 2: Determina el 17% de 540

Forma 1:

• Expresamos el porcentaje en fracción:

¹⁷₁₀₀

• Llamemos  a la cantidad que representa el 17% de 540. Como sabemos que 17 es a 100 como  es a 540, establecemos esta proporcionalidad y nos queda:

¹⁷₁₀₀=^x₅₄₀

• Entonces:

x =^{17 x 540}₁₀₀

x =^9.180₁₀₀

x = 91,8

• • Concluimos que el 17% de 540 es 91,8.

 

Forma 2:

• Expresamos el porcentaje en forma de fracción y calculamos su expresión decimal:

¹⁷₁₀₀= 0,17

• Ahora multiplicamos 540 por la expresión decimal del porcentaje que queremos calcular:

540 x 0.17 = 91,8

• Tenemos, por último, que el 17% de 540 es 91,8.

 

Cómo sacar fácilmente porcentajes: 10%, 25%, 50%, 75% y 200%

Para sacar porcentajes fácilmente vamos a usar la representación fraccionaria del porcentaje y también la expresión decimal del porcentaje.

Cómo calcular fácilmente el 10% de una cantidad

• Recuerda que 10% = ¹⁰₁₀₀
• Si simplificamos esa fracción tenemos que: 10% = ¹⁰₁₀₀ = ¹₁₀
• Ahora, al buscar la expresión decimal de 10% tenemos:10% = ¹₁₀
• Ahora solo debemos multiplicar el número al que le queremos calcular el 10% por la expresión fraccionaria del porcentaje. Fíjate cómo:

Ejemplo 1: Calcula el 10% de 450.

• Multiplicaremos 450 por la expresión fraccionaria de 10% que es 10% = ¹₁₀

 

450 x = ¹₁₀ =  ^{450 x 1}₁₀ =  ⁴⁵⁰₁₀

 

• Ahora calculamos el cociente que indica esta fracción:

 

450 ÷ 10 = 45

• El 10% de 450 es 45

Podemos concluir que:

Ejemplo 2: ¿Cuál es el 10% de 24?

• Para calcularlo vamos a dividir 24 entre 10:

 

24 ÷ 10 = 2,4

• El 10% de 24 es 2,4.

 

Ejemplo 3: Determina el 10% de 23,4

• Dividimos 23,4 entre 10, y tenemos:

 

23,4 ÷ 10 = 2,34

• El 10% de 23,4 es 2,34.

 

 

Cómo calcular fácilmente el 25% de una cantidad

• Sabemos que 25% = ²⁵₁₀₀
• Al simplificar la expresión fraccionaria obtenemos lo siguiente: ²⁵₁₀₀ = ¹₄
• Entonces, para calcular el 25% de cualquier cantidad lo multiplicamos por  ¹₄

Veamos un par de ejemplos.

Ejemplo 1: ¿Cuál es el 25% de 32?

• Para calcularlo vamos a multiplicar 32 por la expresión fraccionaria de 25% que es  ¹₄

32 x ¹₄ =  ³²₄

 

• Ahora calculamos el cociente 32 entre 4:

32 ÷ 4 = 8

 

• El 25% de 32 es 8.

 

Como te has dado cuenta…

 

Ejemplo 2: Calcula el 25% de 220

• Ya sabemos que para calcular el 25% de 220 debemos dividirlo entre 4. Veamos:

220 ÷ 4 = 55

 

• El 25% de 220 es 55

 

Ejemplo 3: Determina el 25% de 50

• Para determinar el 25% de 50 solo tenemos que dividir 50 entre 4.

50 ÷ 4 = 12,5

 

• El 25 % de 50 es 12,5.

 

Cómo calcular fácilmente el 50% de una cantidad

• Empezaremos, al igual que en los casos anteriores, por la representación fraccionaria del porcentaje.

50% = ⁵⁰₁₀₀ =  ¹₂

 

• Ahora sabemos que para calcular el 50% de un número lo multiplicamos por  ¹₂

 

Veamos algunos ejemplos:

 

Ejemplo 1: Calcula el 50% de 630

• Para ello vamos a multiplicar 630 por ¹₂. Veamos:

630 x ¹₂ =  ⁶³⁰₂

 

Ahora calculamos el cociente indicado:

 

• El 50% de 630 es 315

Ejemplo 2: ¿Cuál es el 50% de 531?

• Para calcularlo dividimos 541 entre 2.

541 ÷ 2 = 270,5

• El 50% de 541 es 270,1.

 

Ejemplo 3: Determina el 50% de 806

• Para determinarlo vamos a dividir 806 entre 2.

806 ÷ 2 = 403

• El 50% de 806 es 403.

Cómo calcular fácilmente el 75% de una cantidad

Para saber cómo calcular fácilmente el 75% de una cantidad vamos primero a determinar la expresión fraccionaria del porcentaje.

75% = ⁷⁵₁₀₀ =  ³₄

 

Ahora bien, para calcular el 75% de una cantidad multiplicamos esa cantidad por ³₄.

Vamos a ver algunos ejemplos.

 

Ejemplo 1: Calcula el 75% de 104.

• Para ello multiplicamos 104 por ³₄. Nos queda así:

104 x ³₄ = ^{104 x 3}₄

104 x ³₄ = ³¹²₄

• Ahora calculamos el cociente indicado:

312 ÷ 4 = 78

• El 75% de 104 es 78

 

 

Ejemplo 2: ¿Cuál es el 75% de 762?

• En  este caso multiplicaremos 762 por ³₄.

762 x ³₄ = ^{762 x 3}₄ = ^2.286₄

• • Ahora resolvemos el cociente:

2.286÷ 4 = 571,5

• El 75% de 762 es 571,5

 

Ejemplo 3: Determina el 75% de 120

• • En este caso multiplicaremos 120 por ³₄ .

120 x ³₄ = ^{120 x 3}₄ = ³⁶⁰₄

• • Ahora resolvemos el cociente

360 ÷ 4 = 90

• El 75% de 120 es 90.

 

Cómo calcular fácilmente el 200% de una cantidad

Este porcentaje es muy sencillo de calcular. Vamos a expresarlo de forma fraccionaria para que veas:

200% = ²⁰⁰₁₀₀ = 2

 

Ejemplo 1: ¿Cuál es el 200% de 698?

• Para saber cuál es el 200% de 698 vamos a calcular su doble.

698 x 2 = 1.396

• El 200% de 698 es 1396.

 

Ejemplo 2: Calcula el 200% de 15,6.

• Para calcularlo multiplicamos 15,6 por 2.

15,6 x 2 = 31,2

• El 200% de 15,6 es 31,2,

 

Ejemplo 3: Determina el 200% de 981

• Tal como hicimos en los ejemplos anteriores, para determinarlo vamos a multiplicar 981 por 2.

981 x 2 = 1.962

• El 200% de 981 es 1962.

 

Porcentajes menores o iguales a 100%.

Los porcentajes que son menores al 100% representan una porción de la unidad menor que la unidad misma. Es decir que son una parte menor que la cantidad a la que estamos calculando ese porcentaje.

Por ello, algo importante al considerar cuando calculamos un porcentaje menor a 100% es que el resultado será menor que el número al que le estamos calculando el porcentaje.

Por ejemplo, si un número x es el 12% de 56, entonces  x es menor que 56. Escrito en lenguaje matemático sería: x < 56.

Veamos esto con un ejemplo:

• María estaba calculando el 15% de 360 y el resultado le dio 540.
• Ella se dio cuenta que había cometido algún error porque el 15% de 360 no puede ser mayor a 360.
• Esto fue lo que pensó María al revisar sus cuentas:

 

• María pudo observar que había multiplicado de forma incorrecta porque debía mover la coma un lugar más hacia la izquierda en la multiplicación..
• Entonces rectificó:

360 x 0,15 =54

¡Ahora sí es correcto!

El 15% de 360 es 54.

• Por eso es tan importante conocer esta información sobre los porcentajes menores a 100%.

 

Porcentajes mayores que 100%

Generalmente cuando estudiamos los porcentajes el 100% hace referencia al total o todo, pero existen casos en los que es necesario trabajar con porcentajes mayores que  100%.

Veamos algunos ejemplos de porcentajes mayores que 100%:

 

1. Calcula el 130% de 70.

• Para calcular el 130% procedemos de la siguiente manera: Expresamos el porcentaje en forma de fracción, nos queda:

¹³⁰₁₀₀

• Luego, establecemos esta relación entre la cantidad que representa el 130% de 70 (la  llamaremos x) y el todo que es 70 tenemos entonces.

^x₇₀

• Ahora aplicamos la proporcionalidad que existe entre estas dos expresiones, porque 130 es a 100 como x es a 70:

¹³⁰₁₀₀ = ^x₇₀

• De esta expresión obtenemos que:

x=^{70 x 130}₁₀₀

• Ahora podemos calcular el porcentaje que queremos:

x=^{70 x 130}₁₀₀

x=^9.100₁₀₀

x = 91

• Podemos concluir que el 130 % de 70 es 91.

 

2. El papá de Belén gana mensualmente 1.200 euros. Si su mamá gana el 150% del sueldo de su papá. ¿Cuál es el sueldo de la mamá de Belén?

• Para dar respuesta a la pregunta del problema expresaremos 150% en forma de número decimal, nos queda:

150% = ¹⁵⁰₁₀₀ = 1,5

• Ahora, multiplicaremos 1.200 por 1,5 para calcular el sueldo de la mamá de Belén.

 

1.200 x 1,5 = 1.800

• El sueldo de la mamá de Belén es de 1.800 euros.

 

3. Un elefante al nacer puede pesar aproximadamente 115 kilogramos. Luego, en su edad adulta pesa aproximadamente el 5.200% de su peso al nacer. ¿Cuál es el peso aproximado de un elefante adulto?

• Para determinar el peso aproximado de un elefante adulto, escribiremos 5.200% en forma de número decimal.

5.200% = ^5.200₁₀₀ = 52

• Seguidamente, multiplicamos 52 por el peso del elefante al nacer que es, aproximadamente, 115 kilogramos.

52 x 115 = 5.980

• Con base en los cálculos realizados el peso aproximado de un elefante adulto es de 5.980 kilogramos.

 

Regla de tres simple para porcentajes

La regla de tres simple para porcentajes se aplica en problemas como el siguiente:

 

1. En una clase de cuarto de primaria hay 12 niños y 18 niñas. ¿Qué porcentaje representan los niños de cuarto grado? ¿Y las niñas?

•  Como son 12 niños y 18 niñas, entonces el total o 100% de los estudiantes es 30.
• Para saber el porcentaje que representan los niños de cuarto grado, establecemos una relación de proporcionalidad entre 12 (número de niños) y 30 (total de estudiantes), y conociendo cuál es el 100%, calculamos el valor solicitado.

¹²₃₀ = ^x₁₀₀

• Decimos entonces que 12 es a 30 como x es a 100. Nos queda entonces que:

x = ^{12 x 100}₃₀

• Es decir,  es igual al producto de 12 por 100 dividido entre 30.

x = ^{12 x 100}₃₀

x = 40

• Este mismo problema se puede plantear así:

30  →  100%

12  →  x

• Obteniendo una igualdad similar a la anterior.

x = ^{12 x 100}₃₀
x = 40

• Este último procedimiento es el que se conoce con el nombre de regla de tres simple.

 

Para seguir aprendiendo cómo se aplica la regla de tres simple, realicemos algunos ejemplos más.

 

2. En Estados Unidos de América hay 59 millones de personas de origen  latino, lo que representa el 18% de la población de ese país. ¿Cuántos habitantes en total tiene Estados Unidos de América?

•  Resolvamos este problema aplicando la regla tres simple.

x = ^{59.000.000 x 100}₁₈

x = ^{5.900.000.000}₁₈

x = 327.777.778

• • El número de habitantes de Estados Unidos de América es 327.777.778, aproximadamente.

 

3. El Producto Interno Bruto (PIB) de España para el año 2020 fue de 1.120.000.000.000 de euros, el 5,8% del PIB corresponde a la industria de la construcción. ¿Cuántos euros generó la industria de la construcción en el año 2020?

 

• Resolvemos aplicando la regla de tres simple.

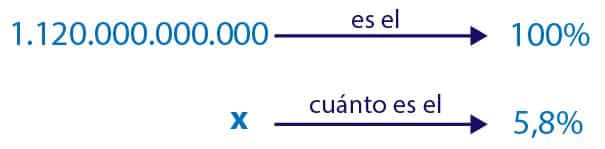
x = ^{1.120.000.000.000 x 5,8}₁₀₀

x = ^{6.495.000.000.000}₁₀₀

x = 64.960.000.000

• • En el año 2020 la industria de la construcción española generó 64.960.000.000 euros.

 

Ejercicios de porcentajes de un número

1.  De los 200 invitados a una boda, asistieron 150. ¿Qué porcentaje de los invitados no asistieron a la boda?

• Planteamos la regla de tres simple.

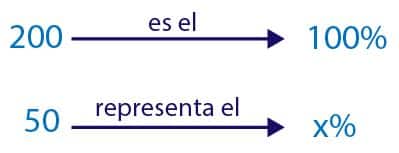
x% = ^{50 x 100}₂₀₀

x% = ^5.000₂₀₀

x% = 25

 

• No asistieron a la boda el 25% de los invitados.

 

2. Durante un partido de baloncesto un jugador ha realizado 25 tiros al aro, encestando la pelota en 18 oportunidades. ¿Cuál es el porcentaje de efectividad de este jugador?

• El jugador ha encestado en 18 de las 25 oportunidades que ha tenido. Esto es:

¹⁸₂₅

• Como queremos saber cuál es el porcentaje asociado a la fracción ¹⁸₂₅ multiplicamos el numerador y el denominador por 4, de tal modo que obtengamos 100 en el denominador.

¹⁸₂₅ = ^{18 x 4}_{25 x 4} = ⁷²₁₀₀

• Ahora aplicamos la definición de porcentaje.

⁷²₁₀₀= 72%

• El porcentaje de efectividad del jugador es 72%.

3. A 30 niños se les preguntó cuál era su deporte favorito. Los resultados obtenidos fueron los siguientes: 9 prefieren el baloncesto, 18 el fútbol y 3 el voleibol. ¿Cuál es el porcentaje de niños que prefiere el fútbol?

• El porcentaje de niños que prefiere el fútbol viene dado por la siguiente fracción:

¹⁸₃₀

• Expresando esta fracción como un número decimal y aplicando la definicón de porcentaje se obtiene:

¹⁸₃₀= 0,6 = ⁶⁰₁₀₀ = 60%

• El 60% de los niños prefiere el fútbol.

 

Cómo calcular porcentajes en una calculadora

Calcular un porcentaje con la calculadora es algo muy sencillo y útil, razón por la que todas las personas deberían saber cómo se hace.

A continuación, te presentamos el paso a paso de cómo sacar porcentajes en calculadora.

Paso 1

Busca tu calculadora. Puede ser una sencilla como la que hay en cualquier tienda, una científica, o la de Windows. La marca o el año no son un problema en este caso.

 

Paso 2

Supongamos que queremos calcular el 40% de 120. Lo primero que debemos anotar en la calculadora es el número al que le queremos aplicar el porcentaje, es decir, 120.

 

Paso 3

Ahora multiplicamos 120 x 40.

Paso 4

Es el momento de presionar la tecla de porcentaje (%). Esta función permite sacar el porcentaje de forma directa.

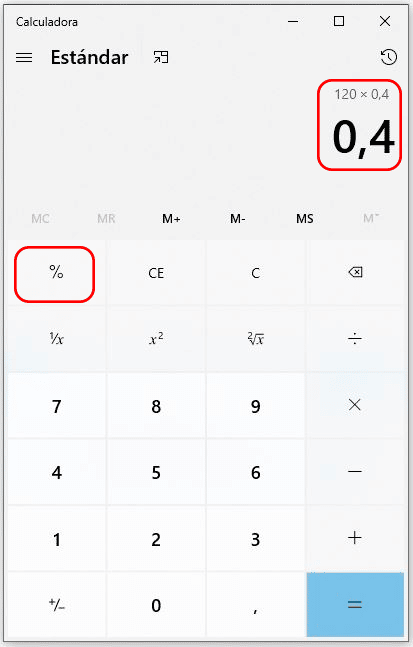
Paso 5

Corresponde pulsar la tecla del signo de igual (=). En este paso aparecerá en la pantalla el 40% de 120.

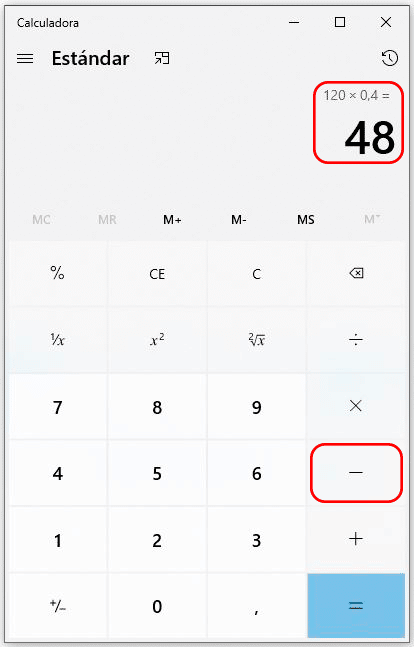
Paso 6

Repite el proceso con otras cantidades y porcentajes.

 

Cómo calcular porcentajes en Excel

Para calcular porcentajes en Excel podemos trabajar de dos formas diferentes. En este apartado te mostraremos esas dos formas. Veamos cómo se hace cada una paso a paso y con imágenes referenciales.

1. Construir una fórmula multiplicando celdas

• Para calcular el porcentaje con Excel construyendo una fórmula en la que se multiplique el valor de dos celdas empezamos haciendo una tabla como la siguiente:

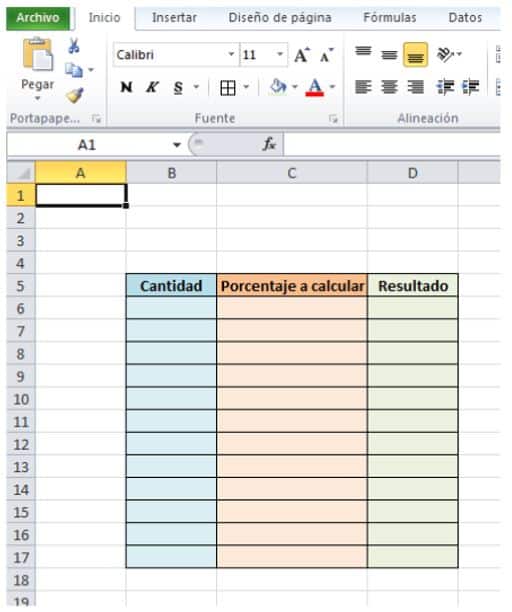
• • En la columna Cantidad (en azul) vamos a escribir las cantidades a las que vamos a calcular el porcentaje.
  • En la columna naranja escribiremos el Porcentaje a calcular.
  • Dejaremos en blanco la columna verde llamada Resultado, que es donde irá el resultado calculado por Excel.

• La tabla quedaría así:

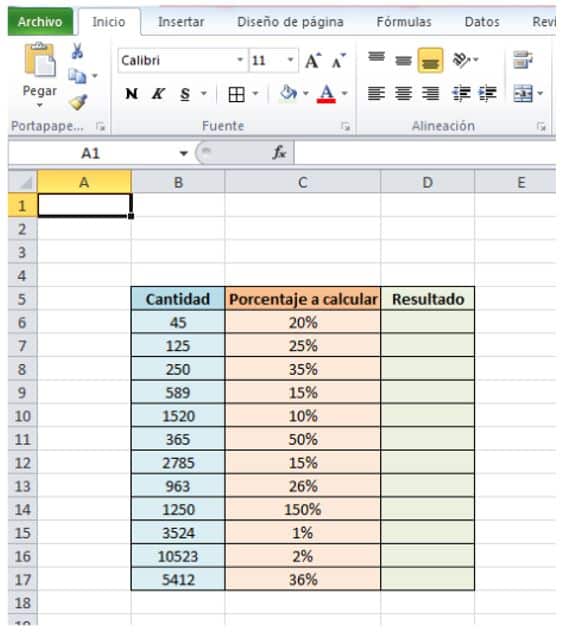
• • Ahora, vamos a escribir la fórmula a utilizar en la columna verde llamada Resultado.
  • Nos situamos en la primera celda vacía de la columna verde, que es la celda D6.
  • Escribimos “=” y hacemos click en la celda con el número “45”, que es la B6.
  • Después escribimos “ * ” y hacemos click en la celda con el 20%, que es la celda C6, y contiene el porcentaje a calcular.

 

• Debería aparecernos en pantalla lo siguiente:

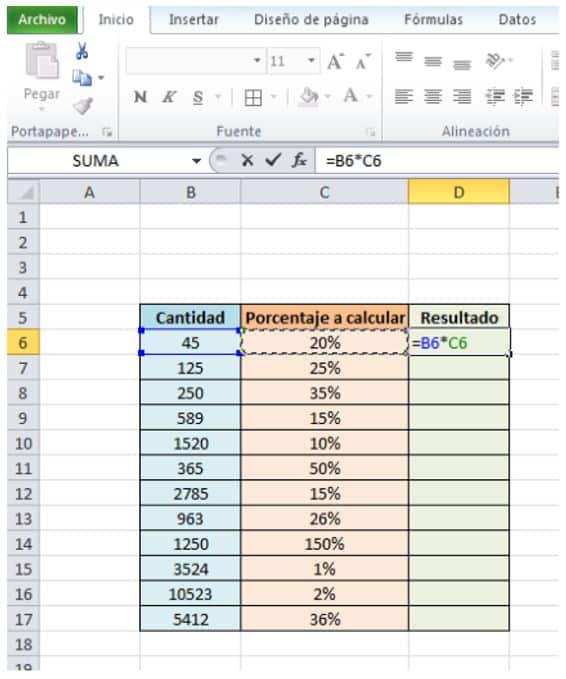
• Ahora presionamos“enter” y obtenemos el resultado en la celda D6.

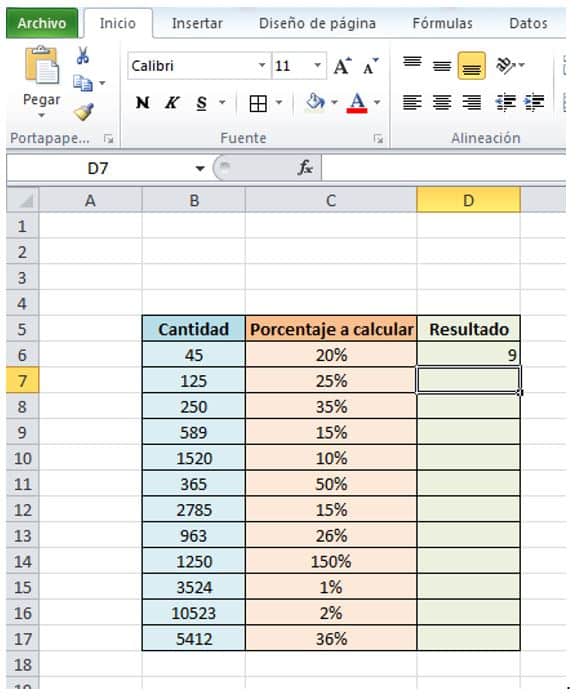
• • Como puedes ver el resultado es correcto pues el 20% de 45 es 9.

 

• Ahora copiamos la fórmula, arrastrando desde la esquina inferior izquierda de la celda D6 que contiene el resultado 9. Recuerda que en esta celda fue donde escribimos la fórmula.

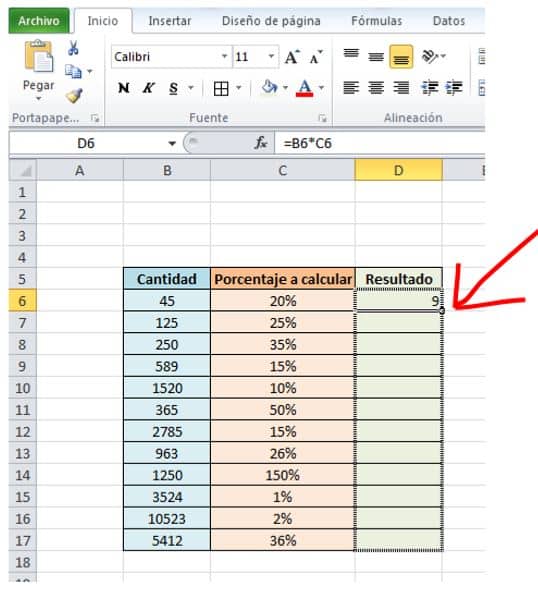
• Como puedes observar ya están listos todos los porcentajes en la columna de resultados.

 

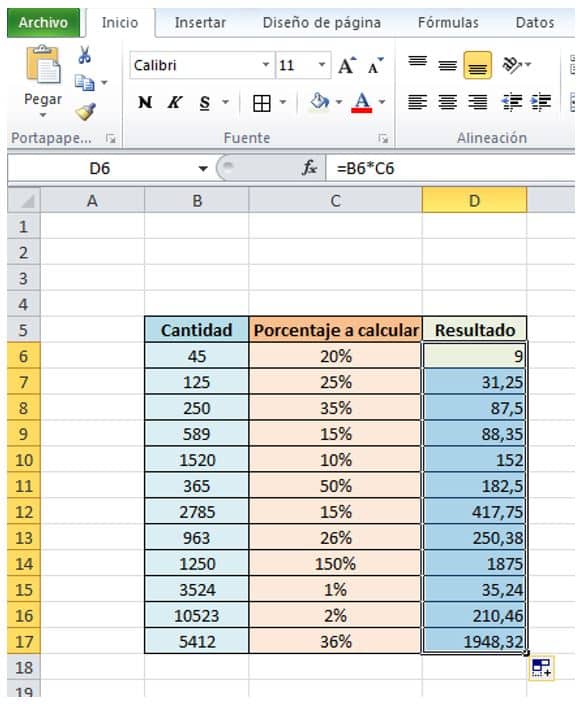
2. Construir una fórmula con el porcentaje incluido

• En este caso vamos a introducir una fórmula que ya incluya el porcentaje.
• Para ello vamos a usar la misma tabla porque queremos que compruebes que obtendremos el mismo resultado.
• Agregaremos una columna que llamaremos porcentaje incluido para que compares con la anterior llamada Resultado.

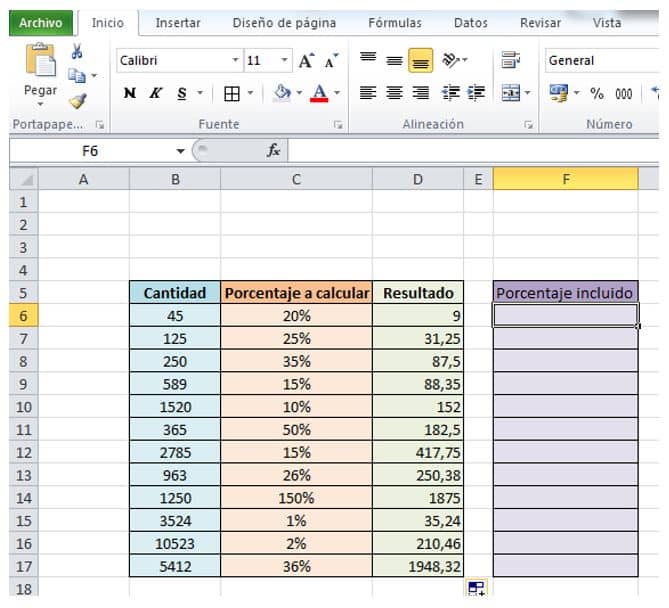
• Ahora, nos situamos en la primera celda vacía de la columna morada, que es la celda F6.
• Escribimos “=” y hacemos click en la celda con el número “45” que es la celda B6.
• Después escribimos “ * ” y “20%” que es el porcentaje que queremos calcular.

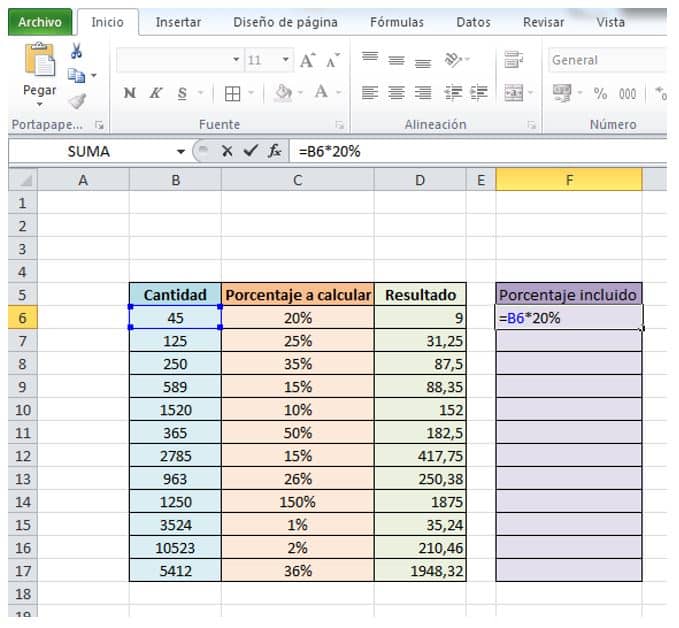
• Presionamos“enter” y obtenemos el resultado.

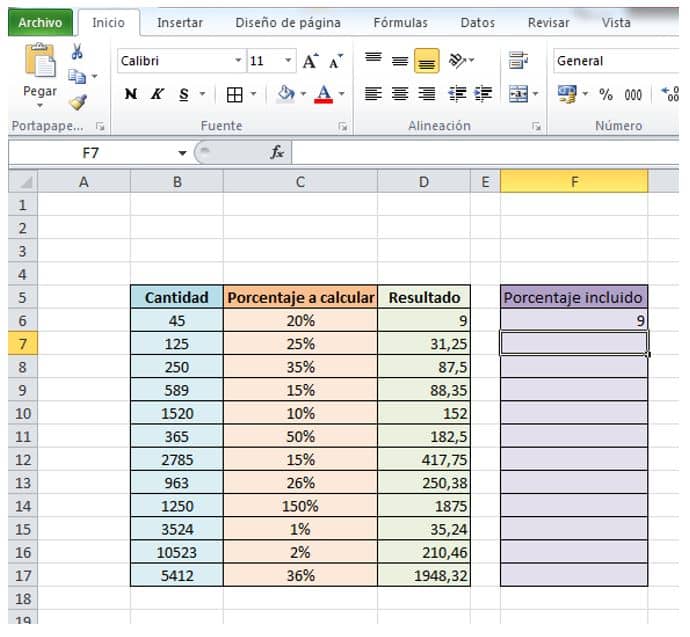
• Ahora repetimos este procedimiento con cada celda de las que sigue.
• Recuerda que debes colocar el porcentaje que deseas calcular en cada caso. Observa dos ejemplos más.
• Aquí estamos calculando el 25% de 125:

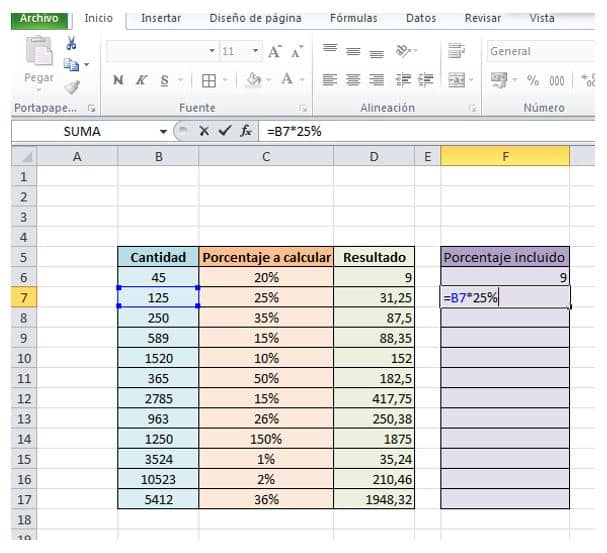
• Y usando ese mismo procedimiento los calculamos todos. También podemos sustituir el porcentaje en número por la celda que lo contiene y, de este modo, al copiar y pegar a todas las celdas se calcularían todos los porcentajes de forma automática.

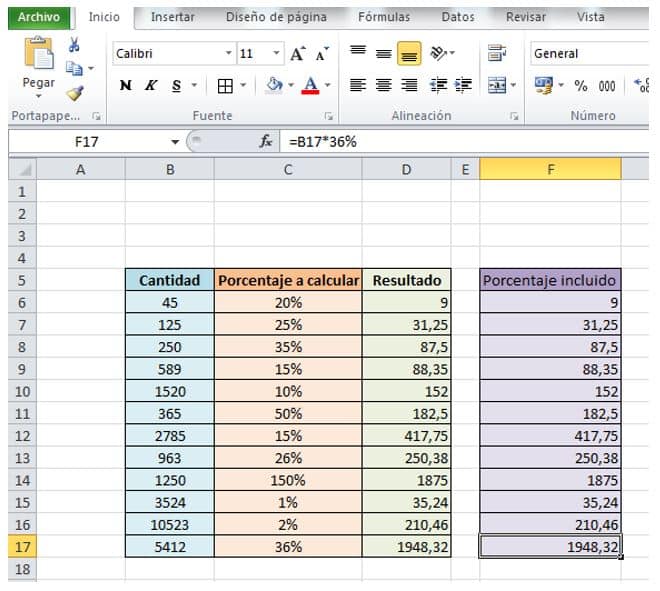
• Como puedes observar, obtuvimos los mismos resultados empleando ambas formas. Tú decides cuál es mejor para ti.

 

Cómo calcular porcentaje de descuento

 Las rebajas son súper famosas entre las personas y consisten en aplicarle un descuento al  precio inicial de un producto. Por ejemplo, si una camisa cuesta 80 euros y tiene un descuento de 25% el precio final de la camisa es  60 euros. En este apartado te explicamos cómo calcular un porcentaje de descuento.

 

Ejemplo 1

• El sueldo de Andrés durante el año 2019 fue de 1.800 € mensuales. En el año 2020 su sueldo disminuyó  a 1.440 € mensuales. ¿Cuál es el porcentaje de descuento que sufrió el sueldo de Andrés?
  • 1.800 € es el 100% y queremos saber en qué porcentaje disminuyó el sueldo de Andrés. Lo primero que hacemos es restar 1.800 € – 1.440 € = 360 €. En el año 2020 Andrés cobró   360 € menos que en 2019.
  • Ahora veamos en qué porcentaje disminuyó el sueldo de Andrés.Para ello plantearemos una regla de tres.

$x\%=\frac{360 x 100}{1800}$

$x\%=\frac{36.000}{1.800}$

$x\% = 20$

• • El sueldo de Andrés disminuyó en un 20%.

 

Ejemplo 2

• Calcular el precio de un teléfono móvil de 200 €, si se le aplica un descuento de 30%.

• • Con un descuento del 30%, pagaremos el 70% del precio inicial.
  • Para conocer cuál es el precio del teléfono luego del descuento, expresamos 70% en forma de número decimal.

$\frac{70}{100} = 0,7$

• • Sabemos por lo que hemos estudiado antes que 0,7 es equivalente a 70%.
  • Ahora multiplicamos
    $200 x 0,7 =140$.
• El precio del teléfono móvil es de 140 €.

 

Ejemplo 3

• El dueño de una tienda anuncia ofertas en toda la mercancía. Ernesto compra un pantalón por 24 € y su precio inicial eran 30 €. ¿Qué porcentaje de descuento se le ha aplicado?
  • Ernesto recibió un descuentro de 6 €.
  • Veamos qué porcentaje representan los 6 €.

$x\%=\frac{6 x 100}{30}$

$x\% = \frac{600}{30}$

$x\% = 20$

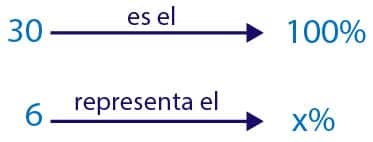
• La tienda ha aplicado un descuento de 20% sobre el precio del pantalón.

 

Cómo calcular porcentaje de aumento

Los porcentajes de aumento tienen que ver con el incremento que tiene una cantidad con respecto a su valor inicial. En este apartado veremos cómo se calcula paso a paso con ejemplos que, fácilmente, puedes ver en la cotidianidad, en las noticias, etc.

1. En el año 2008 la población de España fue 45.668.939 habitantes, para el año 2020 la población era 47.332.614. ¿En qué porcentaje se incremento la población de España en 2020 con respecto a 2008?

• Para dar respuesta a la pregunta de este problema restamos 47.332.614 – 45.668.939 = 1.663.675. El resultado es la variación neta de la población en 2020 con respecto a 2008.
• Ahora calculamos el porcentaje en el que se incrementó la población española en 2020 con respecto a 2008. Para ello utilizaremos una regla de tres simple.

$x\%=\frac{1.663.675 x 100}{47.332.614}$

$x\%=\frac{166.367.500}{47.332.614}$

$x = 3,5\%$

• El porcentaje de incremento de la población de España en 2020 con respecto a 2008, fue de  3,5% aproximadamente.

 

2. El precio de un hotel varió durante estos tres últimos años. El primer año subió un 20%, en el segundo año bajo un 10% y en el tercer año subió un 10%. ¿Cuál es el precio actual del hotel si el inicial era de 100.000 euros?

• Durante el primer año el precio del hotel se incrementó en un 20%, por lo su precio al final de este año fue de 120% del valor inicial.
• Recuerda que 120% se puede expresar como un número decimal. Esto es:

$120\%=\frac{120}{100}=1,2$

• Ahora multiplicamos 1,2 por el precio inicial del hotel que es 100.000 euros.

$1,2 x 100.000 = 120.000$

• • Con base en este último resultado el precio del hotel al cabo del primer año fue de 120.000 euros.

 

• Durante el segundo año el precio bajó un 10%, por lo que el precio del hotel en este año es el 90% de 120.000 euros. Sabemos que:

$90\% = \frac{90}{100} = 0,9$

• Multiplicamos:

$0,9 x 120.000 = 108.000$

• • 108.000 euros es el precio del hotel al cierre del segundo año.

 

• De acuerdo con el planteamiento inicial, en el tercer año el precio del hotel se incrementó en un 10% con respecto al segundo año. Esto quiere decir que el precio del hotel en el tercer año es el 110% de 108.000. Sabemos que:

$110\% = \frac{110}{100} = 1,1$

• Entonces, el precio del hotel al cierre del tercer año es:

$108.000 x 1,1 = 118.800$

• • En conclusión, el precio actual del hotel es 118.800 euros.

 

3. Calcular el porcentaje que aumentó el número de miembros de un club de tenis, si pasó de 80 miembros a 100.

• El club de tenis incrementó el número de miembros en 20. Es decir, pasó de 80 a 100 miembros.

$x\%=\frac{20 x 100}{80}$

$x\%=\frac{2.000}{80}$

$x=25\%$

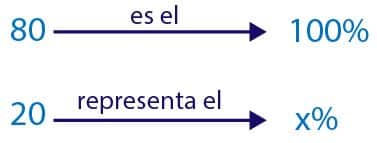
• • El número de miembros del club de tenisse incrementó en un 25%.

 

Resolución de problemas con porcentajes

En este apartado vamos a resolver, paso a paso, problemas con porcentajes.

Problema 1

Una máquina que fabrica tuercas produce un 3% de piezas defectuosas. Si hoy se han apartado 63 tuercas defectuosas, ¿cuántas piezas ha fabricado la máquina hoy?

• Resolución
  • Como nos están preguntando cuál es el total de piezas que ha fabricado la máquina hoy, debemos calcular qué cantidad representa el 100% de las tuercas que se han fabricado.
  • A esa cantidad que debemos calcular, y que representa al 100%, la llamaremos .
  • Nos dan como dato que el 3% de las piezas que fabrican a diario son defectuosas, y hoy han sido 63.
  • De manera que podemos establecer una regla de tres con porcentajes, porque 63 es a 3% como x es a 100%.

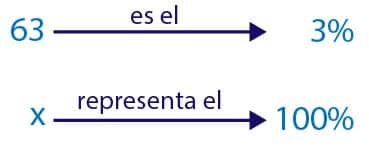
• • De ahí tenemos que:

$x=\frac{63 x 100}{3}$

$x=\frac{6.300}{3}$

x=2.100

• • Como dijimos que x es la cantidad que representa al 3%, podemos decir que ese día la máquina fabricó 2.100 tuercas.

 

Problema 2

De un total de 540 personas encuestadas solamente 108 declaran saber planchar. ¿Qué porcentaje de personas reconocen saber planchar?

• Resolución
  • En este caso debemos saber a qué porcentaje del total corresponde 108. A ese porcentaje desconocido lo llamaremos x.
  • Podemos también establecer una regla de tres con porcentajes para encontrar el porcentaje desconocido (x)

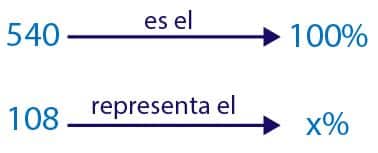
• • Entonces tenemos que:

$x=\frac{108 x 100}{540}$

$x=\frac{10.800}{540}$

$x=20$

• • Recordemos que x representa el porcentaje de personas que declaran saber planchar.
  • Entonces concluimos que el 20% de los encuestados dicen que saben planchar.

 

Problema 3

¿Cuánto  me  costará  un  vestido  de  245  euros  si  me  hacen  una  rebaja  del  15%?

• Resolución
  • Debemos recordar que si nos están haciendo una rebaja del 15% quiere decir que pagaremos 85% del precio del vestido.
  • Además, sabemos que:

$85\%=\frac{85}{100}=0,85$

• • Debemos entonces multiplicar 0,85 por el precio del vestido sin descuento.

$0,85 x 245 =208,25$

• • Podemos concluir que el vestido me costará 208,25 euros.

 

Problema 4

Me compré un pantalón en una tienda en la que todo estaba rebajado en un 30% y pagué por él 79,80 euros. ¿Cuál era el precio del pantalón antes de la rebaja?

• Resolución
  • En este caso, como el pantalón tenía una rebaja del 30%, pagamos el 70% de su precio original.
  • Entonces podemos establecer la siguiente relación:

• • De ahí podemos calcular el valor de x:

$x=\frac{79,80 x 100}{70}$

$x=\frac{7.980}{70}$

$x=114$

• • El precio del pantalón antes de la rebaja era de 114 euros.

 

Problema 5

José Luis ganaba 1.250 euros mensuales y le van a aumentar el sueldo un 5%.  ¿Cuánto ganará José Luis después del aumento?

• En este caso debemos representar primero el aumento de José Luis en porcentajes.

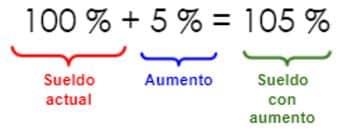
• Este 105% puede escribirse en forma de fracción de esta manera:

$105\%=\frac{105}{100}=1,05$

• Ahora multiplicamos el sueldo actual de Luis José por este número.

$1.250 x 1,05 = 1.312,50$

• Luis José ganará 1312,50 euros después de su aumento de sueldo.

 

Antes de concluir, te dejamos unos cuantos recursos más para que practiques lo aprendido. 

Selecciona un juego 👇 👇 👇